凝聚态场论以及在拓扑相变中的应用(2021/春季)
主讲老师:龚明,物质科研楼C栋812,电话:0551-63606522,邮箱:gongm@ustc.edu.cn
助教:林孝水,物质科研楼C栋810, 邮箱:lxsphys@mail.ustc.edu.cn
上课时间:星期四8-10节(1-16周)
上课地点:2309/2103
- 课程目的
- 熟悉拓扑相变中的相关概念。
- 会计算基本的模型中的拓扑不变量。
- 课程内容框架
- 拓扑绝缘体(动量空间)和磁单极子(实空间)
- 拓扑缺陷:磁性材料中的拓扑缺陷,BKT相变
- 霍尔效应和相关模型:包括几何相等概念
- 拓扑分类
- ………………
- 参考书
- "Gauge Fields, Knots and Gravity",John C. Baez, Javier P. Muniain
- "Topological Insulator: Dirac Equation in Condensed Matter", Shunqing Shen
- "Topological Insulator and Topological Superconductors", B. Andei Bernevig, Taylor L.Hughes
- "A Short Course on Topological Insulators"
- "Geometry, Topology and Physics", M.Nakahara
- "Condensed Matter Field Theory", Alexander Altland, Ben Simons
- Rev.Mod.Phys 中的文献。
- 数学书
- Wiki/知乎
- 有趣的网站分享:The Tensor Product, Demystified
- 考核
- 平时作业 占比 1/2
- Project 占比 1/2 (形式是阅读一篇20页作用的文章,要求电子稿)
- 报告在7月20日23时59分之前交。电子版发邮箱,纸质版物质科研楼810
- 课程报告要求
- Project 推荐论文
推荐文献列表
- 2021年3月18日课程内容
- 杨振宁先生关于规范理论的小短文: C.N. Yang, Phys. Today 67, 11, 45 (2014),中文版本:杨振宁, 汪忠(译), 麦克斯韦方程和规范理论的观念起源
- 什么是\( dxdy\)?
(1) 不是叉乘(量纲)也不是点乘(交换性质)。
(2) 定义为外微分 "\( \wedge \)"
(3) 外微分的性质
a. \(dx\wedge dy = - dy\wedge dx \) (推论\( dx\wedge dx = 0 \) )
b.\( (dx\wedge dy)\wedge dz = dx\wedge (dy\wedge dz) \) (结合律)
c. \(d(dx) = d^2x = 0 \)
- form(形式)
定义和例子
a. 1-form: \( w = \sum_i f_i dx^{i} \)
对应于线。经典力学中的例子: \(dH = \sum_i \dot{q}_i dp_i - \dot{p}_i dq_i \) 统计力学中的例子:\(dU = PdV - TdS + \mu dN \)
b. 2-form: \( w = \sum_{ij} f_{ij} dx^{i}\wedge dx^{j} \)
对应于面。磁通量:\( \oint \mathbf{B} \cdot \mathbf{dS} = \oint \left( B_x dy\wedge dz + \dots \right) \)
c. 3-form: \( w = \sum_{ijk} f_{ijk} dx^{i}\wedge dx^{j}\wedge dx^{k} \)
对应于体
- Stokes 定理.
(1) 微积分中的定义(适用3维空间中的线积分)
\(I = \int_{\gamma}\left( P dx + Q dy + R dz\right) = \iint_{\Sigma} (\frac{\partial R}{\partial y} -\frac{\partial Q}{\partial z} )dydz + (\frac{\partial P}{\partial z} -\frac{\partial R}{\partial x} )dzdx + (\frac{\partial Q}{\partial x} -\frac{\partial P}{\partial y} )dydz \) with \( \gamma = \partial \Sigma \).
(2) 外微分中的定义(适用n维空间中的积分)
\( \int_{\partial \Sigma} \omega = \int_{\Sigma} d\omega \) 或者 \((\partial \Sigma,\omega) = (\Sigma,d\omega)\)
(3) 适用条件
无奇点,被积函数是“光滑”的。例子:复变函数中的留数。
- Topology 是什么?
(1). 放弃了距离概念
(2). 保持了相邻的性质(开集).
一些关于外微分形式在物理上应用的论文: 行列式定义在微分形式中的应用, 外积与外微分运算及其应用, 外微分形式在热力学上的应用
- 课堂笔记:笔记1 ,笔记2,笔记3
- 2021年3月25日课程内容
- 我们关心的物理中的客体
(a).拉氏量 \(L(q_i,\dot{q}_i) \)和哈密顿量\(H(q_i,p_i) \)。 对应于相空间上的函数:\(H: M\rightarrow R\) (其中\(R\)是实数域)
(b).波函数 \(\psi(x)\): 对应于实欧几里德空间到复数域的映射 \(\psi: x \rightarrow C^{N} \)
(c).电场\(\mathbf{E}(x)\)和磁场 \(\mathbf{B}(x)\) :对应于实欧几里德空间到矢量空间中矢量的映射:\(\mathbf{E}: x \rightarrow R^3 \)
(d).周期系统中k空间的Hamiltonian \( H_k = \mathrm{e}^{-\mathrm{i}\mathbf{k}\cdot\mathbf{x}}H \mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{x}}\): 对应于k空间的布里渊区到Hilbert空间中的算符的映射\( H:BZ \rightarrow \hat{A} \)
小结: 许多的物理量都可以抽象为一种映射,而我们关心于某种类型的所有可能映射。
- 数学定义和术语(Ref: Second Chapter, Nakahara)
(a).映射(Map): \(f: X\rightarrow Y \) 其中 \( X,Y \) 是集合。
(b).单射(Injective Map): \(\forall x,x' \in X\), 若有 \(f(x) = f(x') \),则等号当且仅当\(x = x' \)时成立。
(c).满射(Surjective Map): \(\forall y \in Y \) 至少存在一个\(x\in X\)有\(y = f(x)\).
(d).双射(bijection):映射既是单射也是满射(存在逆映射\(f^{-1}\))。
(e).常数映射(Const Map):\( C:X\rightarrow Y\) 其中\(C(x) = y_0 \)
(f).包含映射(Inclusion Map): \(i:A\rightarrow X\) 其中 \(A\subset X\) 记为 \( A \hookrightarrow X\)
(g).恒等映射(Identical Map): \(id_x: X \rightarrow X \) 且有\(id_x(x) = x \)
(h).复合映射(composite map): \( A \stackrel{f}{\longrightarrow} X \stackrel{g}{\longrightarrow} Z \) ,则有 \( z = h(x) = g(f(x))\) 记为 \(h = g\circ f \)
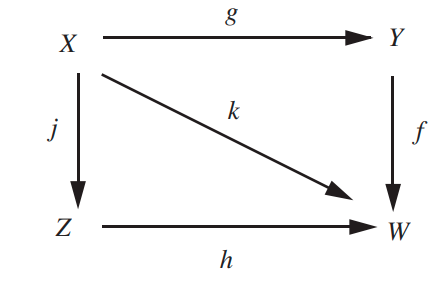
一个交换图的例子。
(i).等价关系(Equivalent): \(A \sim B\): \(A\)等价于\(B\). 具体例子参考课堂笔记。
如何定义等价关系(\( [a] = \{x\in X|x\sim a\}\))?
- \(a\sim a\)
- \( a\sim b \Longrightarrow b\sim a\)
- \( a\sim b,b\sim c \Longrightarrow a\sim c\)
(j).商空间(quotient space) \(\{[x]\} = X/\sim \)
(k).线性空间或矢量空间: 定义(Ref.Defination of Vector Space)
(l).线性映射(Linear Map): 如果一个映射\(f: V\longrightarrow W \)满足 \(f(a_1\mathbf{v}_1 + a_2\mathbf{v}_2 = a_1 f(\mathbf{v}_1)) + a_2 f(\mathbf{v}_2) \)则其被称为线性映射。
(m).像(image): 对于一个映射\(f: V\longrightarrow W \) ,它的像定义为\(f(V) \subset W \)
(n).核(kernels): 对于一个映射\(f: V\longrightarrow W \) ,它的核定义为\(\{ v\in V|f(v)=0\} \)其中\(0\)代表零矢量。
(o).对偶矢量空间(dual vector space):
定义映射\(f: V\longrightarrow K \) 是矢量空间\(V(n,K)\) 在域\(K \)上的一个线性函数。
对于矢量空间中的任意矢量有\(\mathbf{v} = v^i \mathbf{e}_i \),那么根据函数\( f\)的线性性,我们也有\(f(\mathbf{v}) = v^i f(\mathbf{e}_i) \)。显然这些函数\(f(\mathbf{v})\)也会构成一个线性空间,我们称之为\(V(n,K)\)对偶空间\(V^{*}(n,K)\)。而我们也可以定义对偶基矢\( e^{*i}(\mathbf{e}_j) = \delta^{i}_j\).
(p).内积(inner product)和伴随(adjiont)映射:
- 内积: 对偶矢量\( f = f_i e^{*i}\)作用在矢量\(\mathbf{v}\)上,我们将之称为内积\(f(\mathbf{v}) =f_i v^{j}e^{*i}(\mathbf{e}_j) =f_i v^{i} \)。
- 伴随映射:令\(V\)是一个基矢为\(\{\mathbf{e_i} \} \)的矢量空间,且该矢量空间具有同构映射\(g:W\longrightarrow W^{*} \)。对于一个映射\(f: V\longrightarrow W \) ,它的伴随定义为\( \tilde{f} \)
\[
G(\mathbf{w},f \mathbf{v}) = g(\mathbf{v},\tilde{f}\mathbf{w})
\]
(q).Toy index Theorem: 令\(V\) 和\( W\) 是域\(K\)上的一个有限维矢量空间,并且令映射\(f:V\longrightarrow W\)是一个线性映射,则有
\[ \mathrm{dim}\ \mathrm{ker}\ f - \mathrm{dim}\ \mathrm{ker}\ \tilde{f} = \mathrm{dim}\ V-\mathrm{dim}\ W\]
- 课堂笔记:笔记1,笔记2,笔记3
- 2021年4月1日内容
- 对线性空间中的向量进行分类。
(a1). 通过定义映射\(A: R^{m}\longrightarrow R^{n}\) 或者矩阵\(A_{nm}\)。我们将通过\(A\)映射为\(n\)维线性空间\(R^{n}\)中同一个元素\(b\)的 \(m\)维线性空间\(R^{m}\)中的向量\( X \)定义为同一等价类。
(a2). 上述定义也可以理解为我们将线性方程组\(AX = b\)的解\( X\)定义为同一个等价类。
(b). 一个简单的证明: 显然\(R^{m}\)中的向量\(X\)在加法下构成一个群结构。容易证明在映射\(A\)下\( R^{n}\)中的矢量\(b\)可以保持\(X\)的“乘法”。我们称映射\(A\)是两个群之间的同态映射。由同态基本定理我们就知道线性空间\(R^{m}\)可以被映射\(A\)的核作陪集分解。每个陪集都是一个等价类。
概念:正合序列
- 作业1: 若\( A\) 是\( m\times n\)的矩阵。试证明\( Z = tr(\mathrm{e}^{-tA^{\dagger}A}) - tr(\mathrm{e}^{-t A A^{\dagger}})\)和\(t\)无关,且有\( Z = n-m\)是整数。(Index Theorem, Homework Reference: Index calculations for the fermion-vortex system)
- 拓扑空间
- 空间:空间是一些点的集合(set)
- 拓扑空间的定义:\(X\)是集合,\(T\)是集合(X)中的一些子集构成的族\(T =\{u_i|u_i \subset X \}\)。则\((X,T)\)是一个拓扑空间,如果以下的性质成立
(a). \(\varnothing \)和\(X \)是\(T\)中的元素
(b).\(T\)中任意元素的并集仍然是\(T\)中的元素。
(c).\(T\)中有限元素的交集仍然是\(T\)中的元素。
- 拓扑空间的实例
- 拓扑空间中一些概念
(a).近邻/邻域(Neighborhood): 若\(N \)是点\(x\in X\)的邻域,则其应是拓扑空间\((X,T)\)上\(X\)的子集,且应包含至少一个含有\(x\)的开集。\(N\)不一定属于\(T\),但若\( N\)恰好属于\(T\),我们称呼其为开邻域。
(b).Housdroff 空间:对于空间上任意点\(a,b\)存在邻域\(U_a,U_b\)使得\(U_a \cap U_b = 0 \)。
(c).覆盖(Covering)以及开覆盖(Open Covering):拓扑空间\( X \)上的一些子集组成的族\( \{A_i\}\)满足\( \cup_i A_i = X \),则我们称这个族\(\{A_i\}\)是空间\(X\)的一个覆盖。而若\(\{A_i\}\)中的所有元素恰好都是\(T\)中的元素,我们称之为一个开覆盖.
(d).紧致性(Compact):对于任意的开覆盖\(\{U_i|i\in I\}\),都存在一个\(I\)的有限子集\(J\)使得\(\{U_j|j\in J\} \)也是\(X\)的一个覆盖。
(e).One-Point Compactification: \(R^{d} \cup \{\infty \} \simeq S^{d}\)
(f).连通性(Connectedness): 如果一个拓扑空间不能被写为\(X_1\cup X_2 = X \)且其中\(X_1 \cap X_2 = \varnothing\),则该拓扑空间被称为连通的。
(g).同胚(Homeomorphism):如果存在连续的映射\(f:X\longrightarrow Y\)以及连续的逆映射\(Y\longrightarrow X\),则拓扑空间\(X,Y\)是同胚的。
- 拓扑不变量(参考.Topology Invariant)
(a). Euler Number, Chern Number
(b). 代数结构(Group,ring)
(c). 连通性
(d). 紧致性,Hausdroff 性质
(e). 其他
(f1). 问:如何判断两个拓扑空间同胚?答:不清楚
(f2). 两个拓扑空间的上述拓扑不变量相等是这两个空间同胚的充分条件
实例见课堂笔记。
- 流形:局部同构于欧几里德空间。(流形)
- 纤维丛:(参考.Fiber Bundle, 纤维丛)
- 课堂笔记 :笔记1 ,笔记2,笔记3
- 一些龚明老师强调的段落:一点紧致性的重要性,拓扑不变量
- 2021年4月8日内容
- 物理中的闭合曲面
(a). \( R^n \cup \{ \infty \} = S^n\)(通过 One-point compactifaction 将平直空间等效为曲面)
(b). 布里渊区
(c). 圆环 \(\phi \in [0,2\pi) \)
- Geometry Phase/Berry Phase 规范不变的物理量 (Ref:Quantal Phase Factors Accompanying Adiabatic Changes)
(a). 经典力学中的绝热不变量:\(I = \oint \mathbf{p}\cdot \mathbf{dq} \)
(b). 量子力学中的直接推广 \(\gamma = \mathrm{i}\oint\langle m|\mathbf{\nabla_{R}} |m\rangle \cdot \mathbf{d R} \) 。\(\mathbf{p}\rightarrow \mathrm{i}\mathbf{\nabla_R},\mathbf{q}\rightarrow\mathbf{R}\)
(b). 由绝热定理推导出几何相的表达式\(\gamma = \phi(T) - \phi(0) = \mathrm{i}\int_0^{T}\langle m|\frac{\partial}{\partial t}|m\rangle = \mathrm{i}\oint\langle m|\mathbf{\nabla_{R}} |m\rangle \cdot \mathbf{d R} = -\oint \mathbf{A}\cdot\mathbf{dR} \) 和磁矢势有类似形式。
(c). 利用微分形式重写为 \(\gamma = \mathrm{i}\oint \langle m |d |m \rangle \)
(d). 利用规范不变的Berry Curvature写出\(\gamma_m = - \mathrm{Im}\sum_{n\neq m} \oint \vec{dS}\cdot \frac{\langle m|(\vec{\nabla}H)|n\rangle \times\langle n|(\vec{\nabla}H)|m\rangle}{(E_m-E_n)^2} = -\mathrm{Im} \oint
\mathbf{dS}\cdot\mathbf{V_m}(\mathbf{R}(t))\) (TKNN Number)
重要公式: \(\langle m|\nabla|n\rangle = \frac{\langle m|(\nabla H)|n\rangle}{E_n-E_m}, n\neq m \) 以及\([\nabla,H] = \nabla H \)
例子:二能级系统\(\gamma = -\pi (1-\cos \theta)\)对应于闭合轨迹在参数空间的立体角。 形式上等价于参数空间的Monopole \( \mathbf{B} = \frac{\mathbf{R}}{2R^3}\)
(e). Aharonov-Bohm 效应(Ref. 《量子力学》by 曾谨言,一个关于经典带电粒子的运动方程的推导)
(f). Wu-Yang (Ref.Concept of Nonintegrable Phase Factors And Global Formulation of Gauge Fields)
\(\oint_{S^2} \mathbf{B}\cdot\mathbf{dS} = \int_{\Sigma_{up}} \mathbf{B}\cdot\mathbf{dS} +\int_{\Sigma_{down}} \mathbf{B}\cdot\mathbf{dS} = \oint_{\partial\Sigma_{up}} \mathbf{A_1}\cdot\mathbf{dl} +\oint_{\partial\Sigma_{down}} \mathbf{A_2}\cdot\mathbf{dl}\)。将球面上的积分分解为上下半球的积分,之后利用斯托克斯定理转化为曲线积分。
\( \oint_{S^2} \mathbf{B}\cdot\mathbf{dS} = \oint_{\partial\Sigma_{down}}(\mathbf{A_1}-\mathbf{A_2})\cdot\mathbf{dl} = \oint \mathbf{\nabla}\phi\cdot \mathbf{dl} = 2\pi n\)
更简化的版本:复变函数积分中的留数定理。
(g). Geometry phase 在非闭合轨道中总可以通过规范变换的方式消去,一般并不重要。这与闭合轨道的情形并不同。(Ref.Berry phase effects on electronic properties)
- 作业1: 推导非阿贝尔几何相
- 作业2: 推导文献 Theoretical Considerations Concerning Quantized Magnetic Flux in Superconducting Cylinders中的结果
- 阅读材料: 亥维赛和他的科学成就
- 课堂笔记: 笔记1,笔记2
- 曲率
- 2021年4月15日课程内容:
- 相关内容纲要:板书
- 数值计算 Berry Phase(Ref.Takahiro Fukui 1,Takahiro Fukui 2,"Berry Phase, Chern Number"):
(a).错误的做法:直接差分计算 \(\gamma \)。错误的原因是不满足规范不变性。
(b).正确的做法 \(\mathrm{e}^{-\mathrm{i}\gamma} = \exp\{-\oint \langle \psi_{R}|\mathbf{\nabla_{R}}|\psi_{R} \rangle d\mathbf{R}\} = \exp\{-\sum_n [ \langle \psi_{i}|(|\psi_{i+1}\rangle -|\psi_i\rangle )]\} =\prod_i \langle \psi_i|\psi_{i+1} \rangle \). 此做法满足规范不变形。
- Hall Conductance(Ref.实验文章New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance )
(a). 经典霍尔效应:其电导为\( G = \frac{ne}{B} \) 只与载流子密度有关, 和有效质量、相互作用、寿命等无关,所以Hall电导成为了实验上测量电荷密度的标准方法。
(b). 量子霍尔效应:电子的能级变为Landau 能级。系统为平带,存在能隙。体态是完整的绝缘体,但是仔细计算发现会出现边界态,在费米面附近为线性色散关系。
(c). 边界态(edge)的作用(图像): 体态的电子作回旋运动,只有边界态上的电子会碰到壁上,进而沿着边界流动。
(d). 拓扑绝缘体: 体态(bulk)是绝缘体,边界态(edge)是导体。
(e). 电导从经典到量子\( G = \frac{ne}{B} \rightarrow \nu \frac{e^2}{2\pi\hbar}\)。其中\(\nu\)可以是整数也可以是有理数\(\nu=p/q\)。这个结论不平庸,因为这个电导和n,e以及普朗克常数有关,而和磁场无关。此外,它出现在绝缘相,而非金属相中。
- Langhlin's Arguments: 量子化电导和规范不变性相联系 (磁通量子\(\phi_0 = \frac{h c}{e} \)); Laughlin从简单的图像出发,对量子化条件给出了清晰的物理图像。但是这个结论和LL有关,1988年,Haldane构造了另外一个模型证明不需要LL,也有量子化电导。
(a). 第一个公式:\( I = c(\frac{\partial U}{\partial \phi }) = c(\frac{\delta U}{\delta \phi })\)。(细节推导可以在laughlin Nobel Lecture 中找到)
(b). Feyman-Hellman 定理:\(\langle \psi(\phi)|\frac{\partial H}{\partial \phi}|\psi(\phi)\rangle = \frac{\partial U}{\partial \phi} \).
(c). \( I = c\frac{\delta U}{\delta \phi}\) 而 \(\delta U = neV,\delta \phi = \frac{hc}{e}\),则\( I = \nu \frac{e^2}{h}V\)。我们就有量子霍尔电导\(G = \nu \frac{e^2}{h} \)
- Haldane Model(Ref."Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the 'Parity Anomaly'"):
(a).动量空间哈密顿量
\( \mathbf{H}(\mathbf{k})=2 t_{2} \cos \phi\left(\boldsymbol{\Sigma}_{i} \cos \left(\mathbf{k} \cdot \mathbf{b}_{i}\right)\right) \mathbf{I}+t_{1}\left(\boldsymbol{\sum}_{i}\left[\cos \left(\mathbf{k} \cdot \mathbf{a}_{i}\right) \sigma^{1}+\sin \left(\mathbf{k} \cdot \mathbf{a}_{i}\right) \boldsymbol{\sigma}^{2}\right]\right)+\left[M-2 t_{2} \sin \phi\left(\boldsymbol{\Sigma}_{i} \sin \left(\mathbf{k} \cdot \mathbf{b}_{i}\right)\right)\right] \boldsymbol{\sigma}^{3} \)。
注意,非对角部分来自NN相互作用,而两个部分之间的劈裂来自NNN之间的相互作用。Haldane模型成为了理解拓扑绝缘体的重要基础。
其中\(\sigma^{i},i=1,2,3 \)表示泡利矩阵。
(b). 非平庸部分在于规范场。其可以破缺时间反演对称性。
(c). 更简单的模型:QWZ Model的哈密顿量 \( H = \nu (k_x\sigma_x + k_y\sigma_y) + (m-Ak^2)\sigma_z\)(Ref. X. Qi, Phys.Rev.B. 74,085308(2006) )。这个模型可以在正方形格子实现。S. Q. Shen老师的书本上强调,这是超越Dirac最简单的描述。
- 作业1: 模仿Laughlin argument 推导量子化热导 (Ref. Ryota Nakai, Phys.Rev.B. 95,165405 )
- 作业2: 推导Laughlin 论文中LL部分,从LL角度分析能量的改变。
- 阅读材料:
(a). 1998年,Laughlin Nobel Lecture
(b). R.B.Laughlin, Quantized Hall Conductivity in Two Dimensions, Phys.Rev.B. 23,5632(1981)
(c). F.D.M.Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the 'Parity Anomaly, Phys.Rev.Lett.61.2015(1988)
- 课堂笔记:笔记1,笔记2,笔记3
- 2021年4月22日课程内容:
- Haldane Model(1988年Haldane提出,无朗道能级也可以有量子化的霍尔电导。霍尔电导根据TKNN的结果和第一布里渊区的Berry Curvature密切相关。而流形上Curvature的积分数学上被称为Chern Number。Chern Insulator)
(a).系统的哈密顿量
\( H = H_{NN} + H_{NNN}\)。 其中\( H_{NN}\) 与只考虑最近邻跃迁的Graphene模型相同, 而\(H_{NNN} = \sum_{\langle i,j\rangle
}\left(t_2\mathrm{e}^{\mathrm{i}\phi}c^{\dagger}_{iA}c_{jA} + t_2\mathrm{e}^{\mathrm{i}\phi}c^{\dagger}_{iB}c_{jB} + \mathrm{H.c} \right)\)。其中的磁通的形式可以参考原论文。
(b). 次近邻项的作用
(i). 最近邻跃迁只会引入AB原子表象中的非对角项。
(ii). 次近邻跃迁\(t_2 \in \mathcal{R}\)。由于对称性保证,\(\epsilon_{kA} = \epsilon_{kB}\),不会有非平庸的拓扑效应。
(iii). 次近邻跃迁\(t_2 \) 形式上为\(t_2 \mathrm{e}^{\pm \mathrm{i}\phi} \),此时\(\epsilon_{kA} \sim t_2\left(A\cos(\phi)+B\sin(\phi)\right),\epsilon_{kB} \sim t_2\left(A\cos(\phi)-B\sin(\phi)\right) \) 有一个等效的Zeeman劈裂。并且此时Zeeman场是\(k\)依赖的。加入的相位破坏了时间反演不变性,导致了非零的霍尔电导。
(c). 对 Haldane 文章的讨论
(i). \( G = \nu \frac{e^2}{h}\),矢势\(A\)比磁场\(B\)在量子化电导中起着更重要的作用
(ii). 破坏了A,B的对称性,导致有一个等效的Zeeman 劈裂。
(iii). 只考虑最近邻跃迁的石墨烯模型在 Dirac Cone 附近可以近似的写为一个Dirac方程。我们接着考虑加入电磁场情况,通过计算\(\hat{H}^2\)容易可以发现其和连续模型的朗道能级有类似形式,最终我们会发现此体系始终存在一个能量为0的朗道能级。
(iv). 能谱 \( E_k = \epsilon_0(k) + \mathbf{d(k)}\cdot\mathbf{\sigma}\) 形式上总是\(\epsilon = \epsilon_0 \pm |\mathbf{d(k)}| \)是一个两能级系统。类比于\(H = \mathbf{B}\cdot \mathbf{\sigma}\),我们就可以计算系统的拓扑量。
- QWZ Model(Ref. X. Qi, Phys.Rev.B. 74,085308(2006) )比Haldane Model更简单的拓扑绝缘体Model。
(a). 系统的哈密顿量
\[ H = \begin{pmatrix}
c(2-\cos(k_x)-\cos(k_y)-e_s) & \sin(k_y)+ \mathrm{i}\sin(k_x) \\
\sin(k_y) -\mathrm{i}\sin(k_x) & -c(2-\cos(k_x)-\cos(k_y)-e_s)
\end{pmatrix}\]
可以等效为\(H = \mathbf{d}\cdot\mathbf{\sigma}\),其中\( \mathbf{d} = (\sin(k_y),-\sin(k_x),c(2-\cos(k_x)-\cos(k_y)-e_s) ) \)。
(b). 不同的拓扑相的转变点位于能隙关闭点: \( |\mathbf{d}|=0\) 或\( d_x = 0, d_y=0, d_z =0 \)。
不同的拓扑相\[ \sigma_{x y}=\left\{\begin{array}{cc}
1 / 2 \pi, & 0 < e_{s} < 2 \\
-1 / 2 \pi, & 2< e_{s}<4 \\
0, & e_{s}> 4 \ \text{or}\ e_{s}<0
\end{array}\right. \]
(c). Berry Connection 的计算 (\(|\psi\rangle = R \left( u,v \right)^{T} \) with \( R^2(|u|^2+|v|^2=1), R\in \mathcal{R} \))
\[ \mathbf{A} = \mathrm{i}\langle \psi |\mathbf{\nabla_{k}}|\psi \rangle = \mathrm{i} \frac{1}{R}\mathbf{\nabla} R + \mathrm{i} R^2( u^{*}\mathbf{\nabla}u + v^{*}\mathbf{\nabla}v ) = \mathrm{i} \frac{u^{*}\mathbf{\nabla}u + v^{*}\mathbf{\nabla}v }{|u|^2+|v|^2}\]
- SSH Model 和 Jackiw-Rebbi Model(Soliton和Domian Wall的概念,Soliton 对应于零能束缚态。)
(a). Jackiw-Rebbi Model
(i). 哈密顿量为\( H(x) = -\mathrm{i}\hbar\partial_x \sigma_x + m(x) \sigma_z \)
(iii). \(H^2\) 算符形式上为\( H^2 = -d\frac{\partial^2}{\partial x^2} + m(x)^2 + \partial_x m(x)\sigma_z\)。容易知道试探解\( \psi(x) \sim (0,1)^{T} \mathrm{e}^{-\int_{0}^{x} dx' m(x') } \) 一定是一个零能束缚态的解。其对于任意\(m(x)\)都成立。
(ii). 若 \( m(x) = m\ \mathrm{Sign}(x)\), 存在一个零能束缚态,其中心处于Domian Wall 的位置。其解的形式为\( \psi(x) \sim \mathrm{e}^{-m|x|} \)与\(\delta(x)\)势阱的束缚态一致。
(b). SSH Model(物理上对应于聚乙炔链。由Periels 不稳定性产生的新的相)
(i). 哈密顿量 \[ H = -\sum_{n} \left(t_{n,n+1}C^{\dagger}_{n+1}C_{n} + \mathrm{H.c}\right) + \sum_n \frac{1}{2}k^2\left(u_{n+1}-u_{n})^2 \right) + \sum_{n} \frac{1}{2}M (\dot{u}_n)^2 \] with \(t_{n+1,n} = t_0-\alpha(u_{n+1}-u_{n}) \)。
(ii). 对晶格振动采取经典处理。假设\(u_n = (-1)^{n}u\),其中\(u\)是常数,进一步我们有\(\dot{u} = 0\)。那么为晶格的势能\( E_{phonon} = 2Nku^2\),晶格和电子的耦合项则变为\(t_{n,n+1} = t_0 - 2\alpha u(-1)^{n} \)。
(iii). 我们可以求解出基态的能量。容易知道电子和晶格相互作用的能量\(E_{ep} \sim u\),而晶格的势能\(E_{p} \sim u^2 \),当\(u\)比较小时一次方项对能量的贡献占主要部分。此时会导致\(u\)有限时能量的降低,即晶格更倾向于运动来降低能量。
(iv). 两种AB排列的链连接在一起时,会在连接点附近出现束缚态或者称之为(Soliton)。(这个模型和Jackiw-Rebbi模型有密切的联系)。
- 作业1: 对于模型\(H(\mathbf{k}) = d_x(k)\sigma_x+d_y(k)\sigma_y+d_z(k)\sigma_z \) 。使用Mathematica推导模型中的
(a). Connection: \( A_x, A_y \)
(b). Curvature: \(\mathbf{B} = \mathbf{\nabla}\times\mathbf{A} \)
(c). Chen Number: \( \oint_{\Sigma} \mathbf{B}\cdot \mathbf{dS} \) 其中\(\Sigma\)对于QWZ Model 是第一布里渊区。
中的物理量的形式。第一个模型中的参数为 \(\mathbf{d} = (k_x,k_y,A + Bk^2) \)。 Qi-Wu-Zhang Model中参数为[ \( \mathbf{d} = (\sin(k_y),-\sin(k_x),c(2-\cos(k_x)-\cos(k_y)-e_s) ) \)]。
提示:第一题可以用命令\(D[f,x]\),第二题利用FullSimplify,第三题可以作坐标变换为极坐标。
- 作业2: 推导文章(Phys. Rev. Lett. 46, 738(1981))中的结果,理解分数化电荷。
- 阅读材料:
(a). W. P. Su, J. R. Schrieffer, and A. J. Heeger
, "Soliton excitations in polyacetylene", Phys. Rev. B 22, 2099(1980)
(b). W. P. Su, J. R. Schrieffer, and A. J. Heeger,"Solitons in Polyacetylene", Phys. Rev. Lett. 42, 1698(1979)
(c). W. P. Su and J. R. Schrieffer,"Fractionally Charged Excitations in Charge-Density-Wave Systems with Commensurability 3", Phys. Rev. Lett. 46, 738(1981)
- 课堂笔记:笔记1,笔记2,笔记3
- 2021年4月29日内容:
- JR Model 和 Index Theorem (阅读材料: Supersymmetry and the Dirac equation )
(a). \(tr[\mathrm{e}^{-t A A^{\dagger}}] - tr[\mathrm{e}^{-t A^{\dagger} A }] = n - m \)
映射\(A: X \rightarrow Y \),\(A^{\dagger}: Y \rightarrow X \),容易知道 \(A^{\dagger}A: X \rightarrow X,AA^{\dagger}: Y \rightarrow Y \)。
性质:\(A^{\dagger}A,AA^{\dagger} \) 具有相同的非零本征值。由\( AA^{\dagger}|n\rangle = \lambda_n |n\rangle, A^{\dagger}AA^{\dagger}|n\rangle = \lambda_n A^{\dagger}|n\rangle\)容易知道\(A^{\dagger}\)将属于Y空间的\(AA^{\dagger}\)的本征值不等于0的本征矢\(|n\rangle\)映射为X空间中\(A^{\dagger}A\)的本征矢\(A^{\dagger}|n\rangle\)。
(b). JR Model: \[ H = p \sigma_x + m(x)\sigma_y = \begin{pmatrix}0 & p-\mathrm{i}m(x) \\ p+\mathrm{i}m(x) & 0 \end{pmatrix} = \begin{pmatrix} 0 & A \\ A^{\dagger} & 0 \end{pmatrix} \]
我们考虑\(H^2\) 算符,其将上下两个空间中的态各自映射回各自空间.\( H^2 = \begin{pmatrix} A A^{\dagger} & 0 \\ 0 & A^{\dagger} A \end{pmatrix}\)。容易知道其非零本征值一一对应。而零模之间不一定一一对应。一个构造的零能的Ansatz\(|\phi\rangle = C \mathrm{e}^{-\int_0^{x} m(x') dx'} \),易证其满足\((\frac{d}{dx} + m(x))|\phi\rangle = 0 \)
- Band Center 和 Zak Phase
(a). 准动量空间作为参数区间。哈密顿量的形式为\(H(q,t) = \mathrm{e}^{-\mathrm{i}qx}H\mathrm{e}^{\mathrm{i}qx} = \left(p + \hbar q(t)\right)^2/2m + V(x)\)。每个准动量\(q\)都对应一组“瞬时”本征态\( u_{nq(t)}(x)\)。
(b). Wannier 函数 \( |w_{nm}\rangle = \sum_{\mathbf{k}} \mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{R_m}}|\psi_k\rangle = \frac{V}{(2\pi)^d}\int d\mathbf{k}\mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{R_m}}|\psi_{nk}\rangle\)。以及\(|w_{n0}\rangle = \frac{V}{(2\pi)^d}\int d\mathbf{k}\mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{x}}|u_{nk}\rangle \)和\( \hat{x}|w_{n0}\rangle = \frac{V}{(2\pi)^d}\int d\mathbf{k}(-\mathrm{i}) \frac{\partial}{\partial \mathbf{k}}\left(\mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{x}}\right) |u_{nk}\rangle = \mathrm{i}\frac{V}{(2\pi)^d}\int d\mathbf{k} \mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{x}} \frac{\partial}{\partial \mathbf{k}}|u_{nk}\rangle \)
(c). Band Center \( q_n = \langle w_{n0}|\hat{x}|w_{n0}\rangle = \frac{V}{(2\pi)^d}\int d\mathbf{k}\left( \mathrm{i} \langle u_{nk}|\frac{\partial}{\partial \mathbf{k}}|u_{nk}\rangle\right) \) 和Berry Phase有密切联系。我们一般称一维布里渊区上的Berry Phase为Zak Phase。
(d). Anomalous Vecity:\( v_n = \frac{\partial}{\partial k} E_{nk} + \mathrm{i}\left[\langle \partial_q u_n|\partial_t u_n\rangle - \langle \partial_t u_n|\partial_q u_n\rangle \right]\)。
- 流形和微分流形
(a). 流形: 局域上同胚于n维欧几里德空间。
(b). 微分流形: 定义
- 作业1:证明对于一维周期系统,其满足如下关系
(a). 准动量 \(k \in S^1\)
(b). 哈密顿量\( H_k = H_{k+G}\), 其中\(G\) 是倒格式。
要求利用薛定谔方程\(\left(-\frac{d^2}{dx^2} + V(x)\right)\psi_{nk}(x) = E_{nk}\psi_{nk}\),取\( \psi_{nk} = \sum_{m} C_{nk}(G_m) \mathrm{e}^{\mathrm{i}(k+G_m)x} \)。直接从\(C_{nk}\)满足的矩阵等式中得到。
- 阅读材料:
(a). J. Zak, Phys. Rev. Lett. 48, 359(1982)
(b). J. Zak, Phys. Rev. Lett. 62, 2747(1989)
(c). T. Thonhauser, Davide Ceresoli, David Vanderbilt, and R. Resta, Phys. Rev. Lett. 95, 137205(2005)
- 课堂笔记: 笔记1,笔记2
- 2021年5月6日课程内容
- 微分流形: 定义 , Nakahara,Chapter5
(a). 对于坐标卡集中不同坐标卡的共有部分之间存在光滑映射\( f = \phi_i \circ \phi_j^{-1}\)。
(b). 物理规律与坐标的选取无关。流形上点的坐标的选择具有任意性,我们也希望得到一些和坐标无关的量。
- 切向量和切空间
(a). 考虑流形M,且有光滑函数\(f:M \rightarrow R\),流形M上若存在一条轨迹\(x(t)\),显然该轨迹的切向\(\frac{d x(t)}{d t}\)应是坐标无关的。我们可以定义微分算子\(V_p = \frac{d}{dt}\)是曲线\(x(t)\)在p点的切向量。则显然该微分算子作用在函数\(f\)有如下形式 \(\hat{V}f = \sum_i \frac{d x_i}{dt}\frac{\partial}{\partial x_i} f\)或者\(\hat{V}f = \sum_i v_i \frac{\partial}{\partial x_i} f\)。
(b).切空间:切向量构成的线性空间。记为\(T_pM\)。
(c).性质
(1).\(\hat{V}\)和坐标选取无关
(2).\( v^i(p)\)是流形\(M\)到数字的映射
(3).\(\hat{V} \) 是线性空间中的元素。\(\frac{d}{dx_i}\)是基矢\(v_i\)是展开系数。
(4).\(d/dx_i\)是线性独立的。
(5).切向量具有可加性
(6).若\(\hat{V},\hat{W}\)都属于\(T_p M\),则\(\hat{V} +\hat{W}\)属于\(T_p M\),而\(\hat{V} \hat{W}\)不一定属于\(T_p M\),但\([\hat{V} ,\hat{W}]\)属于\(T_p M\)。
- 余切空间
(a).流形上光滑函数\(f\)的变化量\(df = f_q - f_p\)和坐标的选取无关。显然有\(df = \sum_i \frac{\partial f}{\partial y_i} dy_i\)。对于流形上某点\(p\)的所有余切矢量\(df\)也构成一个线性空间\(T_p^{*}M\)
(b).余切空间中的基矢\(dx^i\),系数\(\frac{\partial f}{\partial x_i}\)。
- 切空间和余切空间之间的对偶关系
(a).内积:\( \langle w, v\rangle =\sum_{i,j} v_i \frac{\partial}{x_j} \langle dx^j , \frac{\partial}{\partial x_i}\rangle =\sum_i v_i \frac{\partial}{x_i} \)
(b).余切空间的应用(Ref. Chapter5, "Geometrical methods of mathematical physics")
(b1).热力学中的Maxwell关系 \(dU = TdS - PdV,d(dU) = 0 \rightarrow -\frac{\partial P}{\partial S} = \frac{\partial T}{\partial S}\)
(b2).多变量微积分中的柯西条件\( df = P dx + Q dy \rightarrow \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}\)
(c).流形上积分的计算。各种微分形式都定义在余切空间。
- 张量和form
(a).dxdy 是一个张量,Wedge Product \(dx\wedge dy\)
(b).流形M上\((0,k)\)反对称张量场:微分形式 \(\Omega^{k}(M)\)。
(c).外微分算子\(d\): \(\Omega^{k}(M)\)到\(\Omega^{k+1}(M)\)的映射。
(d).k形式 : 微分形式的定义和相关概念
- 长正合序列和正合序列(相关的图可见课程笔记)
(a).长正合序列:\(\Omega^{0}(M)\rightarrow\Omega^{1}(M)\rightarrow\Omega^{2}(M)\rightarrow\dots\Omega^{n}(M)\rightarrow0 \),其中每个箭头对应一个外微分操作\(d \)。
(a1).闭形式(closed form):\(d\alpha = 0\),恰当形式(exact form):\(\alpha = d\eta\)
(b).正合序列: \(f:A \rightarrow B,\ g:B \rightarrow C\)满足\(\mathrm{Im}f = \ker g\)。正合序列可以对流形上form进行分类。(利用陪集分解)
- 阅读材料:
(a). Nakahara,Chapter5
(b). Chapter5, "Geometrical methods of mathematical physics"
(c). Pierls 相变及其孤子
- 总结: 龚老师总结
- 课堂笔记:笔记1,笔记2
- 2021年5月20日内容
- 群论
(a).群\((G,*) \)要素:
(i). 有恒等元: \(e\)
(ii). 有逆:对于任意元素\(g \in G \)存在\(h \in G\)使得\(gh = e\)
(iii). 在群乘法下封闭: \(\forall g\in G, h\in G\)有\(gh \in G\)
(iv). 满足结合律: \((g h )k = g(hk)\)
(b).例子
(i).实数在加法下构成群:\((R,+)\)。
(ii).n维么正矩阵U_n在矩阵乘法下构成群:\(U(n)\)群。
(iii).对称操作群:长方形对称群\(C_{4v}\),三角形对称群\(C_{3v}\)
(c).基本性质
\(Z_4\)群乘法表
| |
1 |
-1 |
\(\mathrm{i}\) |
\(-\mathrm{i}\) |
| 1 |
1 |
-1 |
\(\mathrm{i}\) |
\(-\mathrm{i}\) |
| -1 |
-1 |
1 |
\(-\mathrm{i}\) |
\(\mathrm{i}\) |
| \(\mathrm{i}\) |
\(\mathrm{i}\) |
\(-\mathrm{i}\) |
-1 |
1 |
| \(-\mathrm{i}\) |
\(-\mathrm{i}\) |
\(\mathrm{i}\) |
1 |
-1 |
(i).重排定理: 如果\(p,b,c \in G\) 和 \(pb = pc\) 然后 \(b = c\)。
(ii).子群:如果一个群\(H\)中所有元素\(h_i\)都是另外一个群\(G\)中的元素,则\(H\)是\(G\)的子群.
(iii).陪集:令\(H = \{ h_1,h_2,\dots\}\)是群\(G\)的子群,\(p\)是群\(G\)中不属于\(H\)的元素.然后我们称\(pH = \{ph_1,ph_2,\dots\}\)的集合为左陪集。
(d).同态基本定理
(i).同态:群\(G\)到群\(G'\)的同态是保持群乘法的映射。如\(g_i \in G \rightarrow g_i' \in G \)并且\(g_1g_2 = g_3\),然后\(g_1'g_2' = g_3'\)
(ii).同态基本定理: 若\(f\)是群\(G\)到\(G'\)的同态映射。若\(K\)是群\(G\)中所有映射为\(G'\)中单位元的元素组成的集合(K = \ker f),那么\(K\)是\(G\)中的一个不变子群。进一步商群\(G/K\)同构于\(G'\)。
(iii).线性代数中的例子:非齐次线性方程组的解可以写为齐次方程的通解以及非齐次部分的特解。
(iv).群中的分类主要有两种:共轭类和陪集。这里我们利用陪集来对集合中的元素进行分类。根据朗道相变理论描述,不同相实际上对应着系统自发破缺了不同的对称性。我们若假设系统的对称性群是\(G\),发生了自发对称性破缺后的相的对称性为\(H\)。那么该相的简并度由商群\(G/H\)描述。而对于系统的不同相,其应由不同的对称群描绘。
- 同伦群(相关概念具体定义可见常见数学概念)
(a).道路同伦
(b).同伦群
- 阅读材料:
(a). Ueda,Chapter12,Topological excitation
(b). Nakahara,Chapter4
(c). "Soft Matter Phyics: An Introduction",Chapter12
- 课堂笔记:笔记1,笔记2
- 2021年5月27日内容
- 数学名词和公式:
- \(\Pi_n(X \times Y) = \Pi_n(X)\times\Pi_n(Y) \)
- \( \Pi_0(X ) = \left\{ \begin{array}{cc} 0 , & X \ \text{is connected} \\ n ,& \text{n is the number of disconnected region in } X \end{array} \right. \)
- 序参量流形的同伦群 \( \Pi_n(G/H) = ? \)。可以利用正合序列计算。
- 长正合序列
\[
\begin{matrix}
\vdots & \vdots & \vdots \\
\rightarrow \Pi_2(H) &\rightarrow \Pi_2(G)& \rightarrow \Pi_2(G/H) \rightarrow \\
\rightarrow \Pi_1(H) &\rightarrow \Pi_1(G)& \rightarrow \Pi_1(G/H) \rightarrow \\
\rightarrow \Pi_0(H) &\rightarrow \Pi_0(G)& \rightarrow \Pi_0(G/H)
\end{matrix}
\]
一般前两列我们是已知的,最后一列待求。我们可以利用短正合序列来计算。
- 短正合序列中的定理和结论
- \(0\rightarrow A\rightarrow B\rightarrow 0 \) 正合 \(\Rightarrow A \simeq B \)
- \(0\rightarrow A\rightarrow B \rightarrow C \rightarrow 0\)正合 \(\Rightarrow B \simeq A \times C\ \text{or}\ B/A \simeq C \)
- 同伦群的例子
- \(S^n \rightarrow S^m\)映射:\(\Pi_n(S^m)\)
\(\Pi_n(S^m)\)
| |
\(\Pi_1 \) |
\(\Pi_2 \) |
\(\Pi_3 \) |
\(\Pi_4 \) |
\(\Pi_5 \) |
\(\Pi_6 \) |
| \(S^1 \) |
\(Z\) |
0 |
0 |
0 |
0 |
0 |
| \(S^2 \) |
0 |
\(Z\) |
\(Z\) |
\(Z_2\) |
\(Z_2\) |
\(Z_2\) |
| \(S^3 \) |
0 |
0 |
\(Z\) |
\(Z_2\) |
\(Z_2\) |
\(Z_2\) |
| \(S^4 \) |
0 |
0 |
0 |
\(Z\) |
\(Z_2\) |
\(Z \times Z_2\) |
| \(S^5 \) |
0 |
0 |
0 |
0 |
0 |
\(Z \) |
- Ueda 书 P381, Eq.12.64 \(N_2 = \oint \mathbf{m}\cdot\mathbf{m}_{\theta}\times\mathbf{m}_{\phi} d\theta d\phi = n l\)
其中\[ \left\{ \begin{array}{c} m_x = \sin(n\theta)\cos(l\phi) \\ m_y = \sin(n\theta)\sin(l\phi) \\ m_z = \cos(n\theta)\end{array}\right.\]
- 李群及其同伦分类
(a).李群的例子
- \(N\times N\)阶可逆矩阵\(A\)构成群\(\det(A)\neq 0\)
- \(N\times N\)阶幺正矩阵构成\(U(N)\)群
- \(N\times N\)阶行列式为\(1\)的矩阵构成\(SU(N)\)群
- \(N\times N\)阶正交矩阵构成\(O(N)\)群
- \(N\times N\)阶行列式为\(1\)的正交矩阵构成\(SO(N)\)群
- SP(2N)群(辛群)
(b).李群的同伦群的举例(表格)
- \(\Pi_n(U(N))\)的表格
\(\Pi_n(U(N))\)
| |
\(\Pi_1 \) |
\(\Pi_2 \) |
\(\Pi_3 \) |
\(\Pi_4 \) |
| \(U(1) \) |
\(Z\) |
0 |
0 |
0 |
| \(U(2) \) |
0 |
0 |
\(Z\) |
\(Z_2\) |
| \(U(3) \) |
0 |
0 |
\(Z\) |
0 |
| \(U(4) \) |
0 |
0 |
\(Z\) |
0 |
| \(U(5) \) |
0 |
0 |
\(Z\) |
0 |
- \(\Pi_n(SO(N))\)的表格
\(\Pi_n(SO(N))\)
| |
\(\Pi_1 \) |
\(\Pi_2 \) |
\(\Pi_3 \) |
\(\Pi_4 \) |
| \(SO(2) \) |
\(Z\) |
0 |
0 |
0 |
| \(SO(3) \) |
\(Z_2\) |
0 |
\(Z\) |
\(Z_2\) |
| \(SO(4) \) |
\(Z_2\) |
0 |
\(Z \times Z\) |
\(Z_2 \times Z_2\) |
| \(SO(5) \) |
\(Z_2\) |
0 |
\(Z\) |
\(Z_2\) |
- \(\Pi_n(RP(N))\)的表格
\(\Pi_n(RP(N))\)
| |
\(\Pi_1 \) |
\(\Pi_2 \) |
\(\Pi_3 \) |
| \(RP^1 \) |
\(Z\) |
0 |
0 |
| \(RP^2 \) |
\(Z_2\) |
\(Z\) |
\(Z\) |
| \(RP^3 \) |
\(Z_2\) |
0 |
\(Z\) |
- Bott周期: \(\Pi_{k}[SO(N)] = \left\{ \begin{array}{cc} 0,& k=2,4,5,6 mod(8) \\ Z_2, & k=0,1 mod(8) \\ Z,& k=3,7 mod(8) \end{array}\right. \)
- 序参量流形:\(M = G/H\)。其他名称:(a).Goldstone 定理 (b). stablizer group (c). little group (d). orbital group (e). quatiant group
- 例子:Spin BEC。系统的对陈群\(G = SO(3)\times U(1)\),铁磁相\((1,0,0)^{T}\),保持序参量不变的子群\(U(1)\)。序参量流形\(M = G/H = SO(3)\)。其同伦群如下
\(\Pi_n(SO(3))\)
| |
\(\Pi_1 \) |
\(\Pi_2 \) |
\(\Pi_3 \) |
\(\Pi_4 \) |
| \(SO(3) \) |
\(Z_2\) |
0 |
\(Z\) |
\(Z_2\) |
- 课堂笔记:笔记1,笔记2
- 2021年6月3日内容
- 同伦群的应用
- Fermion, Boson, and Anyon
(a). 这个分类实际上和对\(RP^{d-1}\)的同伦分类联系在一起.
(b). \(\Pi_1(RP^{d-1})=\left\{ \begin{array}{cc} 0,& d=1 \\
Z,& d=2 \\
Z_2,& d=3
\end{array}\right. \)
(c). 考虑两个可分辨粒子的体系\(\psi(r,R)\),质心自由度\(R\)在 \(R^d\) 空间. 相对运动自由度\(r\)在 \((R^d-\{0\})\) 空间。但如果我们考虑两个全同的例子, 相对运动的自由度就处于 \(\left(R^d-\{0\}\right)/Z_2 \simeq R^{+}\times S^{d}/Z_2 \simeq R^{+}\times RP^{d-1}\)空间。此空间的第一阶同伦群如上。
- 液晶中的缺陷
(a). Half Vortex:\( \mathbf{d} \): (i).\( \mathbf{d} \)和\( -\mathbf{d} \)等价。(ii) \(\Pi_1(R^{+}\times S^d/Z_2)\simeq \Pi_1( S^d/Z_2) = \Pi_1(RP^d) \)
- 单极子 (Dirac Monopole,Wu-Yang Monopole,Shankar Monopole
,t' Hopf Monopole)
(a).Dirac Monopole: 磁场\(\mathbf{B}=g\frac{\mathbf{r}}{r^3}\),矢势\(\mathbf{A} = \frac{g}{r(r-z)}\left(y,-x,0\right) = -\frac{g(1+\cos(\theta))}{r\sin(\theta)}\mathbf{e}_{\phi}(\mathbf{r})\)。由此矢势产生的磁场有一条具有奇异性的Dirac弦\(\mathbf{\nabla}\times\mathbf
{A} = g\frac{\mathbf{r}}{r^3}\ - 4\pi g \delta(x)\delta(y)\theta(z)\mathbf{e}_z\)。
(b).Wu-Yang Monopole:
(c).Shankar Monopole(Shankar Skymion): 存在于氦3超流A相中。 速度场可以写为
\(\mathbf{\Omega} = f(\mathbf{r})\mathbf{r}/r\), with \(f(\mathbf{r}) = \left\{ \begin{array}{cc} 2\pi,& r=0 \\ 0,& r\rightarrow\infty \end{array}\right.\) ,\(\Pi_3(SO(3))= Z \)
(d).Skymion: d = 3,\(\Pi_3(S^2)=Z\);
- 对拓扑缺陷的分类(分类):
Defects in different spatial dimension
| |
d=1 |
d=2 |
d=3 |
d=4 |
| \(Pi_0\) |
point |
line |
surface |
\(\cdot\) |
| \( Pi_1 \) |
texture |
point |
line |
surface |
| \( \Pi_2 \) |
|
texture |
line |
surface |
- 拓扑绝缘体的分类
- 如何描述量子霍尔效应的体系。
- \(H = U^{\dagger}\begin{pmatrix} \mathbf{1}, 0\\ 0,\mathbf{1} \end{pmatrix} U \)
- 阅读材料:
(a).Rui Yu et.al,"Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection", Phys.Rev.B 84,075119(2011)
(b).Y. X. Zhao and Z. D. Wang, "Topological Classification and Stability of Fermi Surfaces", Phys.Rev.Lett. 110, 240404(2013)
(c).Y. X. Zhao, Andreas P. Schnyder, and Z. D. Wang, "Unified Theory of PT and CP Invariant Topological Metals and Nodal Superconductors", Phys. Rev. Lett. 116, 156402(2016)
- 课堂笔记:笔记1
- 2021年6月10日内容
- 态空间中的几何性质
- 单比特系统的密度矩阵 \(\rho = \frac{1}{2}\left(1 + \mathbf{a}\cdot\mathbf{\sigma} \right) \),由于\(\mathrm{Tr}(\rho)=1\)以及\(\mathrm{Tr}(\rho^2)\leq 1\),\(\mathbf{a}\)所处空间的性质就可以确定。
- 对于纯态,\(\mathbf{a}\)处于Bloch球的球面\(S^2\)上。对于混态,\(\mathbf{a}\)处于Bloch球包裹的球体中\(S^2\times[0,1]\)。
- 可以利用代数方法求出其序参量流形或者态空间。我们可以将单比特系统的密度矩阵写为
\(\rho = T\lambda T^{\dagger}\),其中\(\lambda = diag(p,1-p)\)。我们容易发现对于对于所有混态的密度矩阵,其可以由\([0,1]\times T,\ T \in U(2)\)生成,而纯态则是\(\{0,1\}\times T \)。这就是此系统的\(G\)。我们容易发现对于某个特定的\(\rho\),其生成矩阵\(T\)实际上具有一定的冗余自由度\(T\simeq T \times diag(\exp(\mathrm{i}\theta_1),\exp(\mathrm{i}\theta_1))\)。这代表这个系统的\(H = U(1)\times U(1)\),那么我们就得到了该系统的序参量流形是\(M = ([0,1]\times U(2))/(U(1)\times U(1)) \simeq S^2 \)
- Bott周期律和重要的数学结论
- \(\Pi_n(S^n) = Z \) and \(\Pi_k(S^n) = 0 \) if \( k < n \)
- \(\Pi_k(U(N)) = \Pi_k(U(1)\times SU(N)) = \left\{ \begin{array}{cc} 0,& k = 2n \\ Z,&k=2n+1 \end{array} \right.\)
- \(\Pi_k(O(N)) = \Pi_k(SO(N)) = \left\{ \begin{array}{cc} 0,& k = 2,4,5,6 mod(8) \\ Z_2 ,& k=0,1 mod(8) \\ Z,& k = 3,7 mod(8) \end{array} \right.\)
- \(\Pi_k(SP(N)) = \left\{ \begin{array}{cc} 0,& k = 0,1,2,6 mod(8) \\ Z_2 ,& k= 4,5 mod(8) \\ Z,& k = 3,7 mod(8) \end{array} \right.\)
- Bott证明 \( \left\{ \begin{array}{cc} \Pi_k(SP/U) &= \Pi_{k+1}(SP) \\ \Pi_k(U/O) &= \Pi_{k+2}(SP) \\ \Pi_k(O/U) &= \Pi_{k+1}(O) \\ \Pi_k(U/SP) &= \Pi_{k+2}(O) \end{array} \right. \)
- 定义Stiefel Manifold为 \( \left\{ \begin{array}{ll} V_{k,N} &= SO(N)/SO(N-k) \\ V_{k,N}^{C} &= U(N)/U(N-k) \\ V_{k,N}^{H} &= SP(N)/SP(N-k) \end{array} \right. \)。可以证明 \(\left\{ \begin{array}{ll} \Pi_i(V_{k,N}) &= 0 \\ \Pi_i(V_{k,N}^{C}) &= 0 \\ \Pi_i(V_{k,N}^{H}) &= 0 \end{array} \right. \)。
- 序参量流形的同伦群(求表)
- \( H = U \Sigma U^{\dagger}\) 其中\(\Sigma = \begin{pmatrix} 1_N & 0 \\ 0 & 1_{M} \end{pmatrix}\),仿照单比特系统的做法,我们容易知道此系统的稳定子群为\( M = U(N+M)/(U(N)\times U(M))\)。对于N和M非常大时\(\Pi_i(U(N))\)是稳定的。
-
正合序列表
| i |
\(\Pi_i(U(M)) \) |
\(\Pi_i(U(N+M)/U(N)) \) |
\(\Pi_i(U(N+M)/(U(N))\times U(M)) \) |
| 5 |
\(Z\) |
0 |
0 |
| 4 |
0 |
0 |
\(Z\) |
| 3 |
\(Z\) |
0 |
0 |
| 2 |
0 |
0 |
\(Z\) |
| 1 |
\(Z\) |
0 |
0 |
| 0 |
0 |
0 |
|
- 拓扑绝缘体的分类表格 (Ref. Shinsei Ryu et.al, "Topological insulators and superconductors: tenfold way and dimensional hierarchy", New J. Phys. 12,065010(2010) )

- 时间反演不变性: 反幺正算符\(T = U K \),其中\(K\)是复共轭算符。\(TpT = -p,TxT = x\)。
- 阅读材料:
(a). Adelman,"The Geometry of state space"
(b). Alexander Altland and Martin R. Zirnbauer, "Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures", Phys. Rev. B 55, 1142(1997)
- 课堂笔记:
- 课堂笔记:笔记1笔记2
- 2021年6月17日内容
- 历史
(a). Wigner, 1951,1958
(b). Dyson, 1962
(c).随机矩阵的提出。
- 离散对称性(时间反演对称性、粒子空穴对称性、手征对称性)
- 时间反演对称性\(T = U_{T}K \),其中\(K\)是复共轭算符\(U_T\)是幺正算符。其满足\(T^2 = \pm 1,TH = HT\)。
(a).\(T^2 = 1\):保证波函数可以取为实数。 e.g. \(T = K, T = \sigma_x K, T = \sigma_z K \)
(b).\(T^2 = -1\):在此条件下由\(|\phi\rangle,T|\phi\rangle\)是哈密顿量\(H\)的具有同一本征值的简并态。Kramers简并 e.g.\(T = \mathrm{i} \sigma_y K \)
- 粒子空穴对称性\(C = U_{C}K \),其满足\(CH = -HC \),同理有\(C^2 = \pm 1\)
(a).\(C^2 = 1\)如:\(C = \tau_x K\),\(C^2 = -1 \)如:\(C = \tau_y K\)
- 手征対称性
(a). \( S = CT = U_C U_T^{*} \)。
(b). 存在\(T\)对称和\(C\)对称,一定存在\(S\)对称。存在\(T\)和\(S\)一定存在\(C\),存在\(T\)和\(C\)一定存在\(S\) 由此给出了对称性存在的类型的限制。
- 为什么是十重分类
(a).所有对称性都没有:1
(b).具有C对称性和T对称性,其一定具有S对称性。根据\(T^2 = \pm 1, C^2 = \pm 1\): 4
(c).C对称性和T对称性只具有一种:4
(d).只具有S对称性: 1
(a).\(1+4+4+1=10\)
- BdG 方程
(a). 对于一个超导的哈密顿量 \(H = \sum_{\alpha,\beta} \left(h_{\alpha,\beta} c_{\alpha}^{\dagger}a_{\beta} + \frac{1}{2} \Delta_{\alpha\beta} c^{\dagger}_{\alpha} c_{\beta}^{\dagger} + \frac{1}{2}\Delta_{\alpha\beta}^{*} c^{\dagger}_{\alpha} c_{\beta}^{\dagger} \right)\).我们可以将其写成一个BdG形式\(H_{\mathrm{BdG}} = \frac{1}{2} \begin{pmatrix} h & \Delta \\ \Delta^{\dagger} & -h^{T} \end{pmatrix} \)。
(b).由于\(\Delta^{T} = -\Delta \),则BdG哈密顿量一定具有粒子空穴对称性。
(c). 在保证对角化后粒子性质不变的前提下,BdG哈密顿量的形式是唯一的。
- 阅读材料:
(a). Alexander Altland and Martin R. Zirnbauer, "Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures", Phys. Rev. B 55, 1142(1997)
- 课堂笔记:笔记1
- 2021年6月24日内容
- Lie 群和Lie 代数
- 群的四要素:(i).封闭 (ii).单位元 (iii).逆元 (iv).结合律
- Lie群:具有群结构的流形,一般情况下可以被参数化的群是李群。e.g. \(U(N) = \{U|U^{\dagger}U = 1 \}\)以及\(SU(N) = \{U|U \in U(N)\ \& \det(U) = 1 \}\)和\(O(N) = \{O|O^{T}O = 1 \}\)
- O(N)群的另一种表述 \(O^{T}O=1\)或者\(O^{T}MO = M,M = M^{\dagger} = M^{\dagger},M^2 = 1\)
- 辛群(Sympletic Group): SP(N) ,\(U^{\dagger}U = 1,U^{T}\epsilon U = \epsilon, \epsilon = \mathrm{i}\sigma_y, \epsilon^{T} = -\epsilon,\epsilon^2=-1 \)
- Topological 分类:首先我们将哈密顿量\(H\)映射为平带\(\tilde{H} \),其中\(H\)具有的Lie群是Hamilonian Space,\(\tilde{H} \)具有的Lie群是Classfication Space。
- D Class(BdG方程)
(a). 哈密顿量具有的形式\(H = \begin{pmatrix} h& \Delta \\ \Delta^{\dagger} & -h^{T} \end{pmatrix} \)。定义\(\Sigma_x K\),其中\(\Sigma_x = \begin{pmatrix} 0& 1_{n} \\ 1_n & 0 \end{pmatrix}\)。
(b). 定义\(X = \mathrm{i}H\),容易证明\(X^{\dagger} = -\mathrm{i}H^{\dagger} = -\mathrm{i}H = - X = \Sigma_x X^{T} \Sigma_x \)。进一步有\(CXC^{-1} = C\),类似时间反演不变的系统\(THT^{-1} = H\)
(c). 若\(X,Y\)满足\(X^{\dagger} = -X = \Sigma_x X^{T}\Sigma_x,Y^{\dagger} = -Y = \Sigma_x Y^{T}\Sigma_x\)容易证明\(Z = [X,Y]\)也满足上述关系,即\( Z^{\dagger} = -Z = \Sigma_x Z^{T}\Sigma_x\)。
(d).和C类的比较: \(\left\{ \begin{array}{cc} C = \Sigma_x K &\rightarrow C^2 = 1 \\ C = \Sigma_y K &\rightarrow C^2 = -1 \end{array}\right.\)
- C Class ,可以证明\(U\in SP(2N)\)
- 一个小表格
Summary
| |
T |
C |
S |
H |
M = G/N |
| A |
0 |
0 |
0 |
U(2N) |
U(N+M)/U(N)\times U(M) |
| D |
0 |
+1 |
0 |
SO(2N) |
SD(N+M)/U(N) |
| C |
0 |
-1 |
0 |
SP(2N) |
SP(2N)/U(N) |
- Topological index
(a). Winding number
\(\frac{1}{2\pi\mathrm{i}}\oint \frac{dz}{z} \) 到矩阵 \(I = \frac{1}{2\pi\mathrm{i}}\oint Tr(U^{-1}dU)\)
(b). Chern-Character
规范势\(A^{ab}(k) = A_{\mu}^{ab}(k)dk^{\mu} \langle U^{-}_a(k) | d |U^{-}_b(k) \rangle\)。对应的规范场\(F = dA + A^2\)
可以定义Chern特征标\(ch_{n+1} = \frac{1}{(n+1)!}tr(\frac{\mathrm{i}F}{2\pi})^{n+1} \),或者\(CH(F) = \sum_n ch_{n+1} \simeq Tr(\mathrm{e}^{\frac{\mathrm{i}F}{2\pi}}-1) \)
- 阅读材料:
(a). 时间反演对称性,Sakurai
(b). Alexander Altland and Martin R. Zirnbauer, "Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures", Phys. Rev. B 55, 1142(1997)
- 课堂笔记: 笔记1
- 2021年7月4日内容
- 如何构造一个具有时间反演不变形的哈密顿量
- \(H =\begin{pmatrix} h_1(\mathbf{k}) & t(\mathbf{k})\\ t^{\dagger}(\mathbf{k}) & h_2(\mathbf{k}) \end{pmatrix}\), 其中 \(t^{T}(\mathbf{k}) = -t(-\mathbf{k}) \) 以及 \(h_2^{*}(-\mathbf{k}) = h_1 (\mathbf{k}) \)
- 时间反演算符\(\theta = \begin{pmatrix}0 &-\mathrm{i} \\ \mathrm{i} & 0 \end{pmatrix}K \),利用\(\theta H(k) = H(-k)\theta \)的关系容易证明以上条件。
- Ando 推导中用到的重要公式
- 辅助矩阵\(W_{\alpha\beta}(k) = \langle u_{\alpha,-k}|\theta|u_{\beta,k}\rangle \)
(a). \( \langle u_{\alpha,-k}|\theta|u_{\beta,k}\rangle + \langle u_{\beta,k}|\theta|u_{\alpha,-k}\rangle = 0 \)
(b). 在\(k=0,k=\pi\)点。有\(W^{T} + W = 1\),以及\(W = \begin{pmatrix} 0 & -\exp(-\mathrm{i}\chi) \\ \exp(-\mathrm{i}\chi) & 0 \end{pmatrix} = -\mathrm{i}\sigma_y \exp(-\mathrm{i}\chi) \)
(c).幺正性:\(WW^{\dagger} = 1 \)
(d).两组完备关系:\(|u_{\alpha,-k}\rangle = \sum_{\beta} W_{\alpha\beta}^{*}\theta|u_{\beta k}\rangle\)以及\( \langle u_{\alpha,-k}| = \sum_{\beta} W_{\alpha\beta}\langle u_{\beta k}|\theta^{\dagger} \)
- Connection \( a_{\alpha,\beta}(k) = -\mathrm{i}\langle u_{\alpha k}| \nabla_k |u_{\beta k}\rangle\)
(a). 一个结论\( U(-k) = W(k)a(k)W^{\dagger}(k) + \mathrm{i}W(k)\nabla_k W^{\dagger}(k)\)
(b). 定义\( A = tr(a) \),则\(A(-k) = A(k) + \mathrm{i}tr(W\nabla_k W^{\dagger})\)
- \((-1)^{p_{\theta}} = \frac{\sqrt{\det(W(0))}}{Pf(W(0))}\frac{Pf(W(\pi))}{\sqrt{\det(W(\pi))}} \)。更一般化的有\((-1)^{\mu} =\prod_i \frac{\sqrt{\det(W(K_i))}}{Pf(W(K_i))}\)
- Z2拓扑不变量和底流形的同伦分类具有紧密联系。
(a). Z2 和 \(RP^d\)的同伦分类,以及 Rui Yu等人的argument。
(b). Z2的边缘态和 \((-1)^{\mu} =\prod_i \frac{\sqrt{\det(W_i)}}{Pf(W_i)}\)
- 阅读材料:
(a). Liang Fu and C. L. Kane, "Time reversal polarization and a Z2 adiabatic spin pump", Phys. Rev. B 74, 195312(2006)
(b). Yoichi Ando, "Topological Insulator Materials", Phys. Rev. B 74, 195312(2006)
(c). Rui Yu et.al, "Equivalent expression of Z2 topological invariant for band insulators using the non-Abelian Berry connection", Phys.Rev.B 84,075119(2011)
(d). J. Zak,"Berry’s phase for energy bands in solids", Phys. Rev. Lett. 62, 2747(1989)
- 课堂笔记:笔记1
USTC
BBS