数学概念 | 定义 | 物理例子 |
| 切丛(tangent bundle) | \(m\)维流形\(M\)上的切丛\(TM\)是\(M\)上所有切空间的集合: \(TM\equiv \bigcup_{p\in M} T_{p}M\), \(M\)为基空间. | 经典力学中速度场与实空间构成切丛 |
| 纤维丛(fibre bundle) | 纤维丛\((E,\pi,M,F,G)\)包含以上元素: (i)微分流形\(E\)称为全空间(total space);(ii)微分流形\(M\)称为基空间(base space);(iii)微分流形\(F\)称为纤维(fibre)或典型纤维(typical fibre);(iv)满射\(\pi: E\to M\)称为投影映射(projection), 其逆像\(\pi^{-1}(p)=F_{p}\cong F\)称为\(p\)处的纤维;(v)Lie群\(G\)称为结构群(structure group), 左作用于\(F\);(vi)\(M\)的一组开覆盖\( \{U_{i}\}\)具有微分同胚\(\phi_{i}: U_{i}\times F\to \pi^{-1}(U_{i})\), 使得\(\pi\circ\phi_{i}(p,f)=p\). 映射\(\phi_{i}\)被称为局部平凡化(local trivialization), 因为\(\phi_{i}^{-1}\)将\(\pi^{-1}(U_{i})\)映射到直积\(U_{i}\times F\); (vii)如果写出\(\phi_{i}(p,f)=\phi_{i,p}(f)\), 则映射\(\phi_{i,p}: F\to F_{p}\)是一个微分同胚. 当\(U_{i}\cap U_{j}\neq\varnothing\)上, 要求\(t_{ij}(p)\equiv \phi_{i,p}^{-1}\circ \phi_{j,p}: F\to F\)是\(G\)的元素. 然后\(\phi_{i}\)和\(\phi_{j}\)由光滑映射\(t_{ij}: U_{i}\cap U_{j}\to G\)联系起来: \[\phi_{j}(p,f)=\phi_{i}(p,t_{ij}(p)f)\] 映射\(t_{ij}\)称为转移函数(transition functions). | |
| 截面(section, or cross section) | 令\(E\stackrel{\pi}{\longrightarrow}M\)为纤维丛. 截面\(s: M\to E\)是满足\(\pi\circ s=\mathrm{id}_{M}\)的光滑映射. | |
| 丛映射(bundle map) | 令\(E \stackrel{\pi}{\longrightarrow} M\)和\(E^{\prime} \stackrel{\pi^{\prime}}{\longrightarrow} M^{\prime}\)为纤维丛. 将光滑映射\(\bar{f}: E^{\prime} \rightarrow E\)称为丛映射, 如果它将\(E^{\prime}\)上的每条纤维\(F_{p}^{\prime}\)映射到\(E\)上的\(F_{q}\)上. \(\bar{f}\)自然产生一个平滑映射\(f: M^{\prime} \to M\)使得\(f(p)= q\). 可交换 可交换 | |
| 等价丛(Equivalent bundle) | 如果存在一个丛映射\(\bar{f}: E^{\prime} \rightarrow E\)使得\(f: M\to M\)是恒等映射并且\(\bar{f}\)是一个微分同胚, 则两个丛\(E^{\prime} \stackrel{\pi^{\prime}}{\longrightarrow} M\)和\(E \stackrel{\pi}{\longrightarrow} M\)是等价的. 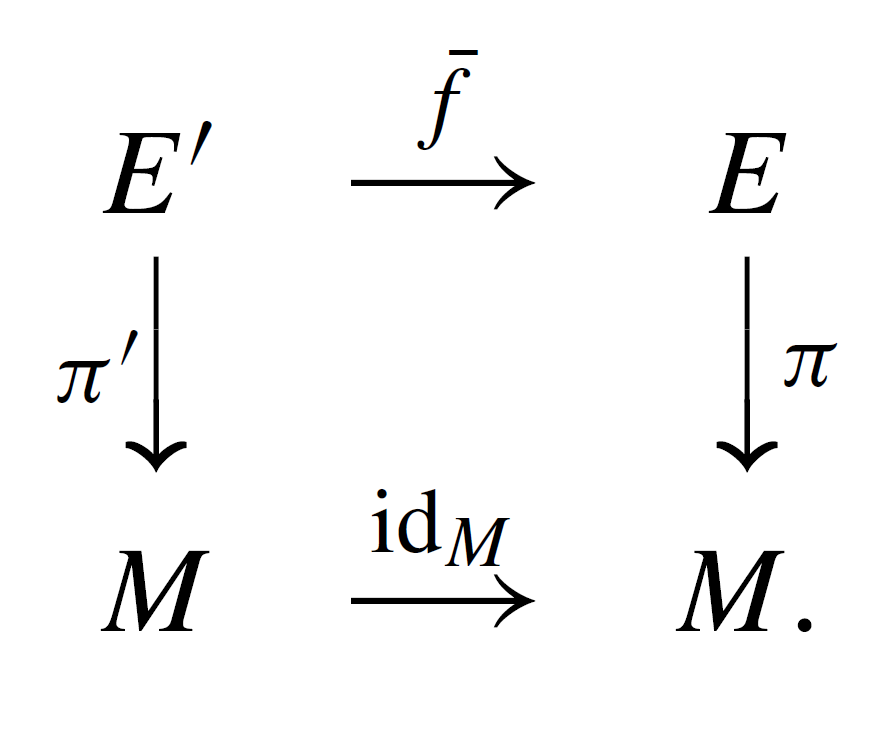 | |
| 拖回丛(Pullback bundle) | 令\(E \stackrel{\pi}{\longrightarrow} M\)为具有典型纤维\(F\)的纤维丛. 如果给出映射\(f: N\to M\), 则pair \((E,f)\)在具有相同纤维\(F\)的\(N\)上定义新的纤维丛. 令\(f^{*}E\)是\(N\times E\)的子空间, 它由点\((p,u)\)组成, 使得\(f(p)=\pi(u)\). \(f^{*} E \equiv\{(p, u) \in N \times E \mid f(p)=\pi(u)\}\)称为\(E\)上\(f\)的拉回. \(f^{*}E\)的纤维\(F_{p}\)只是\(E\)的纤维\(F_{f(p)}\)的一个拷贝. 如果我们用\(\pi_{1}:(p, u) \mapsto p\)定义\(f^{*} E \stackrel{\pi_{1}}{\longrightarrow} N\), 用\(\pi_{2}:(p, u) \mapsto u\)定义\(f^{*} E \stackrel{\pi_{2}}{\longrightarrow} E\), 可以使拉回\(f^{*}E\)具有纤维丛的结构, 我们得到以下丛映射. 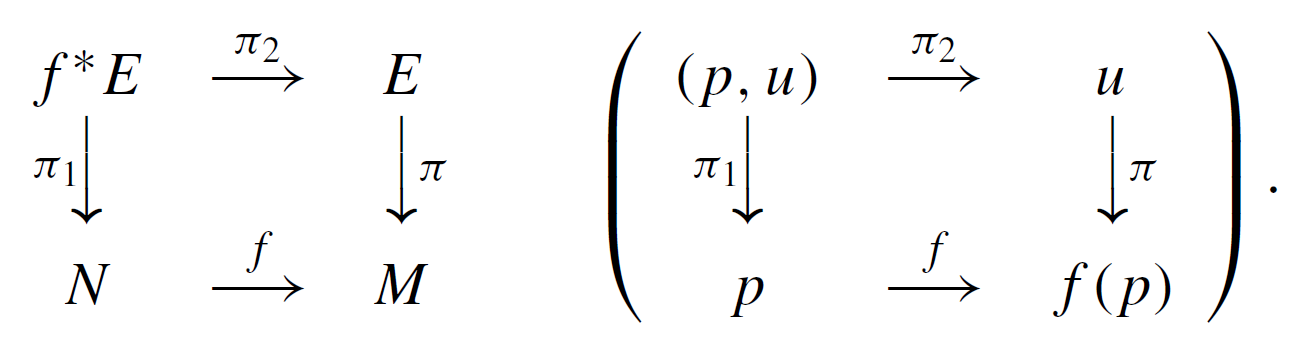 | |
| 向量丛(vector bundle) | 向量丛\(E \stackrel{\pi}{\longrightarrow} M\)是纤维为向量空间的纤维丛. 令\(F\)为\(\mathbb{R}^{k}\), \(M\)为\(m\)-维流形. 尽管全空间\(E\)为\(m+k\)维, 但通常将\(k\)称为纤维维度, 并用\(\mathrm{dim} E\)表示. 转移函数属于\(\mathrm{GL}(k,\mathbb{R})\), 因为它将向量空间同构地映射到相同维数的另一个向量空间上. 如果\(F\)是复向量空间\(\mathbb{C}^{k}\), 则结构群为\(\mathbb{GL}(k,\mathbb{C})\). | 线丛(line bundle): 纤维为一维\((F=\mathbb{R} \text{or} \mathbb{C})\)的向量丛称为线丛. |
| 标架(frame) | 令\(E \stackrel{\pi}{\rightarrow} M\)为向量丛, 其纤维为\(\mathbb{R}^{k}\)(或\(\mathbb{C}^{k}\)). 在图册\(U_{i}\)上, \(\pi^{-1}(U_{i})\)是平凡的, \(\pi^{-1}\left(U_{i}\right) \cong U_{i} \times \mathbb{R}^{k}\), 我们可以选择\(k\)个线性独立的\(U_{i}\)上的截面\(\left\{e_{1}(p), \ldots, e_{k}(p)\right\}\). 这些截面定义了\(U_{i}\)上的标架. | 在切丛\(TM\)上, 每根纤维都具有由图册\(U_{i}\)上的坐标系\(x^{\mu}\)给出的自然基\(\left\{\partial / \partial x^{\mu}\right\}\). 如果\(M\)被赋予度量, 我们也可以使用正交基\(\left\{\hat{e}_{\alpha}\right\}\). \(\partial / \partial x^{\mu}\)或\(\left\{\hat{e}_{\alpha}\right\}\)是\(U_{i}\)上的向量场, 集合\(\left\{\partial / \partial x^{\mu}\right\}\)或\(\left\{\hat{e}_{\alpha}\right\}\)在\(U_{i}\)上形成线性独立的向量场. 总是可以在\(U_{i}\)上选择\(m\)个线性独立的切向量, 但是在\(M\)上不一定是这种情况. 根据定义, 基向量的分量是
\[\begin{array}{c}
\partial / \partial x^{\mu}=(0,\quad \ldots, \quad 0, \quad 1, \quad 0, \quad \ldots, \quad 0) \\
\qquad\qquad \mu
\end{array}\]
或
\[\begin{array}{c}
\hat{e}_{\alpha}=(0, \quad \ldots, \quad 0, \quad 1, \quad 0, \quad \ldots, \quad 0). \\
\qquad \alpha
\end{array}\] |
| 余切丛(cotangent bundle) | 余切丛\(T^{*} M \equiv \bigcup_{p \in M} T_{p}^{*} M\)的定义与切丛类似. 在坐标为\(x^{\mu}\)的图册\(U_{i}\)上, 将\(T_{p}^{*} M\)的基取为\(\left\{\mathrm{d} x^{1}, \ldots, \mathrm{d} x^{m}\right\}\), 它是\(\left\{\partial / \partial x^{\mu}\right\}\)的对偶. 设\(y^{\mu}\)为\(U_{j}\)的坐标, 以使\(U_{i} \cap U_{j} \neq \emptyset\). 对于\(p \in U_{i} \cap U_{j}\), 有变换,
\[\mathrm{d} y^{\mu}=\mathrm{d} x^{\nu}\left(\frac{\partial y^{\mu}}{\partial x^{\nu}}\right)_{p}.\]
1-形式\(\omega\)在所有坐标系中都可以表示为
\[\omega=\omega_{\mu} \mathrm{d} x^{\mu}=\tilde{\omega}_{\mu} \mathrm{d} y^{\mu}\]
可见
\[\tilde{\omega}_{\mu}=G_{\mu}^{v}(p) \omega_{\nu}\]
其中\(G_{\mu}^{\nu}(p) \equiv\left(\partial x^{\nu} / \partial y^{\mu}\right)_{p}\)对应于转换函数\(t_{ji}(p)\).
| |
| 乘积丛(product bundle) | 令\(E \stackrel{\pi}{\rightarrow} M\)和\(E^{\prime} \stackrel{\pi^{\prime}}{\rightarrow} M^{\prime}\)为向量丛, 其纤维分别为\(F\)和\(F^{\prime}\). 乘积丛
\[E \times E^{\prime} \stackrel{\pi \times \pi^{\prime}}{\longrightarrow} M \times M^{\prime}\]
是典型纤维是\(F \oplus F^{\prime}\)的纤维丛.
相应地, \(F \oplus F^{\prime}\)上的向量可以写为
\[\left(\begin{array}{c}
V \\
W
\end{array}\right) \quad \text { where } V \in F \text { and } W \in F^{\prime}\]
向量加法和标量乘法定义为
\[\left(\begin{array}{c}
V \\
W
\end{array}\right)+\left(\begin{array}{c}
V^{\prime} \\
W^{\prime}
\end{array}\right)=\left(\begin{array}{c}
V+V^{\prime} \\
W+W^{\prime}
\end{array}\right), \qquad \lambda\left(\begin{array}{c}
V \\
W
\end{array}\right)=\left(\begin{array}{c}
\lambda V \\
\lambda W
\end{array}\right) \]
| |
| Whitney和丛(Whitney sum bundle) | 令\(E \stackrel{\pi}{\rightarrow} M\)和\(E^{\prime} \stackrel{\pi^{\prime}}{\rightarrow} M\)是向量丛, 分别具有纤维\(F\)和\(F^{\prime}\). Whitney和丛\(E \oplus E^{\prime}\)是\(E\times E^{\prime}\)在\(f: M\to M\times M\)的拖回丛, \(f\)定义为\(f(p)=(p,p)\)
 因此, \(E \oplus E^{\prime}=\left\{\left(u, u^{\prime}\right) \in E \times E^{\prime} \mid \pi \times \pi^{\prime}\left(u, u^{\prime}\right)=(p, p)\right\}\). Whitney和丛的纤维是\(F \oplus F^{\prime}\).
因此, \(E \oplus E^{\prime}=\left\{\left(u, u^{\prime}\right) \in E \times E^{\prime} \mid \pi \times \pi^{\prime}\left(u, u^{\prime}\right)=(p, p)\right\}\). Whitney和丛的纤维是\(F \oplus F^{\prime}\).
| |
| 张量积丛(tensor product bundle) | 令\(E \stackrel{\pi}{\rightarrow} M\)和\(E^{\prime} \stackrel{\pi^{\prime}}{\rightarrow} M\)是\(M\)上的向量丛. 通过将纤维张量积\(F_{p} \otimes F_{p}^{\prime}\)分配给每个点\(p\in M\)来获得张量积丛\(E \otimes E^{\prime}\). 如果\(\{e_{\alpha}\}\)和\(\{f_{\beta}\}\)是\(F\)和\(F^{\prime}\)的基, 则\(F \otimes F^{\prime}\)由\(\left\{e_{\alpha} \otimes f_{\beta}\right\}\) spanned, 因此\(\operatorname{dim}\left(E \otimes E^{\prime}\right)=\operatorname{dim} E \times \operatorname{dim} E^{\prime}\). | |
| 主丛(principal bundle) | 主束具有与结构群\(G\)相同的纤维\(F\). 主丛\(P \stackrel{\pi}{\longrightarrow} M\)也由\(P(M,G)\)表示, 通常也称为\(M\)之上的\(G\)-丛. | 令\(P\)为具有纤维\(\mathrm{U}(1)=S^{1}\), 底空间\(S^{2}\)的主丛 —— magnetic monopole \(\mathrm{SU}(2)\) instanton |
| 伴丛(associated bundle) | 给定主纤维丛\(P(M,G)\), 可以定义伴纤维丛. 令\(G\)左作用于流形\(F\). 定义\(g\in G\)作用于\(P\times F\)为
\[(u, f) \rightarrow\left(u g, g^{-1} f\right)\]
其中\(u\in P\), \(f\in F\). 伴纤维丛\((E, \pi, M, G, F, P)\)为等价类\(P\times F/G\), 两点\((u,f)\)和\((ug,g^{-1}f)\)是等效的.
| 标架丛(frame bundle)自旋丛(spin bundle) |
| 联络(connection) | 令\(P(M,G)\)为主丛. 在\(P\)上的联络是一种唯一的分离: 将切空间\(T_{u}P\)唯一地分离为垂直子空间\(V_{u}P\)和水平子空间\(H_{u}P\), 使得
(i)\(T_{u} P=H_{u} P \oplus V_{u} P\).
(ii)\(P\)上的光滑向量场\(X\)被分离为光滑向量场\(X^{H} \in H_{u} P\)和\(X^{V} \in V_{u} P\), 且\(X=X^{H}+X^{V}\).
(iii)对于任意\(u \in P\)和\(g \in G\), 有\(H_{u g} P=R_{g *} H_{u} P\).

| |
| 联络1-形式(connection one-form) | 联络1-form \(\omega\in \mathfrak{g}\otimes T^{*}P\)是\(T_{u}P\)在垂直分量\(V_{u}P\simeq \mathfrak{g}\)上的投影. 投影属性归纳为以下要求,
(i) \(\omega\left(A^{\#}\right)=A\), \(A \in \mathfrak{g}\)
(ii) \(R_{g}^{*}\omega=\mathrm{Ad}_{g^{-1}}\omega\)
因此, 对于\(X\in T_{u}P\),
\[R_{g}^{*}\omega_{ug}(X)=\omega_{ug}(R_{g*}X)=g^{-1}\omega_{u}(X)g.\]
| Ehresmann联络 |
| 规范势(gauge potential) | | \(\mathrm{U}(1)\)规范理论, Dirac磁单极子, Aharonov-Bohm效应, Yang-Mills理论, 瞬子(instanton), Berry相 |
| 规范变换(gauge transformation) | | |
| 水平提升(horizontal lift) | 令\(P(M,G)\)为\(G\)丛, 设\(\gamma: [0,1]\to M\)为\(M\)中的曲线. 曲线\(\tilde{\gamma}: [0,1]\to P\)被称为\(\gamma\)的水平提升, 如果\(\pi \circ \tilde{\gamma}=\gamma\), 且\(\tilde{\gamma}(t)\)的切向量始终属于\(H_{\tilde{\gamma}(t)} P\). | |
| 平行输运(parallel transport) | 令\(\gamma: [0,1]\to M\)为曲线. 取点\(u_{0}\in \pi^{-1}(\gamma(0))\). 经过\(u_{0}\)存在\(\gamma(t)\)的唯一水平提升\(\tilde{\gamma}(t)\), 因此有唯一点\(u_{1}=\tilde{\gamma}(1)\in \pi^{-1}(\gamma(1))\). \(u_{1}\)点称为\(u_{0}\)沿着曲线\(\gamma\)的平行输运. | |
| 和乐群(parallel transport) | 取点\(u\in P\)满足\(\pi(u)=p\), 并考虑在\(p\)处的回路集合\(C_{p}(M)\): \(C_{p}(M)\equiv\{\gamma: [0,1]\to M|\gamma(0)=\gamma(1)=p\}\). 元素集合
\[\Phi_{u}\equiv \{g\in G|\tau_{\gamma}(u)=ug, \gamma\in C_{p}(M)\}\]
是结构群\(G\)的子群, 并称为\(u\)点的和乐群.
| |
| 协变导数(covariant derivative) | 令\(\phi \in \Omega^{r}(P) \otimes V\), \(X_{1}, \ldots, X_{r+1} \in T_{u} P\). \(\phi\)的协变导数定义为
\[\mathrm{D} \phi\left(X_{1}, \ldots, X_{r+1}\right) \equiv \mathrm{d}_{P} \phi\left(X_{1}^{H}, \ldots, X_{r+1}^{H}\right)\]
其中\(\mathrm{d}_{P} \phi \equiv \mathrm{d}_{P} \phi^{\alpha} \otimes e_{\alpha}\).
| |
| 曲率张量(curvature tensor) | 协变导数一般不对易,
\[[D_{\mu}, D_{\nu}]=-F_{\mu\nu}^{a}\tilde{V}_{a}\]
其中\(F_{\mu\nu}^{a}=\partial_{\mu}A_{\nu}^{a}-\partial_{\nu}A_{\mu}^{a}+f_{bc}^{a}A_{\mu}^{b}A_{\nu}^{c}\)称为曲率张量
| Yang-Mills场强 |
| 曲率2-形式(curvature two-form) | 曲率2-形式\(\Omega\)是联络1-形式\(\omega\)的协变导数,
\[\Omega \equiv \mathrm{D} \omega \in \Omega^{2}(P) \otimes \mathfrak{g}\]
| Yang-Mills场强 |
| Cartan结构方程(Cartan's structure equation) | 令\(X, Y \in T_{u} P\). \(\Omega\)和\(\omega\)之间满足Cartan结构方程
\[\Omega(X, Y)=\mathrm{d}_{P} \omega(X, Y)+[\omega(X), \omega(Y)]\]
或者写为
\[\Omega=\mathrm{d}_{P}\omega+\omega\wedge\omega.\]
| |
| Ambrose–Singer定理(Ambrose–Singer theorem) | 令\(P(M,G)\)是连通流形\(M\)上的\(G\)丛. 点\(u_{0}\in P\)的和乐群\(\Phi_{u_{0}}\)的Lie代数\(\mathfrak{h}\)与有如下形式的元素张成的\(\mathfrak{g}\)子代数一致
\[\Omega_{u}(X, Y) \qquad X, Y \in H_{u} P\]
其中\(a\in P\)是与\(u_{0}\)在相同水平提升上的点.
| |
| 曲率的局域形式(local form of the curvature) | 曲率\(\Omega\)的局域形式\(\mathcal{F}\)定义为
\[\mathcal{F} \equiv \sigma^{*} \Omega\]
其中\(\sigma\)是定义在流形\(M\)的图册\(U\)上的局域截面(\(\mathcal{A}=\sigma^{*} \omega\)). \(\mathcal{F}\)可以用规范势\(\mathcal{A}\)表示为
\[\mathcal{F}=\mathrm{d} \mathcal{A}+\mathcal{A} \wedge \mathcal{A}\]
其中, \(\mathrm{d}\)是\(M\)上的外导数.
| |
| Bianchi恒等式(Bianchi identity) | \[\mathrm{D}\Omega=0\]. | |
| 对称迹(symmetrized trace) | \[\begin{aligned}
\tilde{P}\left(A_{1}, A_{2}, \ldots, A_{r}\right) &=\operatorname{str}\left(A_{1}, A_{2}, \ldots, A_{r}\right) \\
& \equiv \frac{1}{r !} \sum_{P} \operatorname{tr}\left(A_{P(1)}, A_{P(2)}, \ldots, A_{P(r)}\right)
\end{aligned}\] | |
| 陈-Weil定理(Chern-Weil theorem) | 令\(P\)是不变多项式. \(P(\mathcal{F})\)满足
(a)\(\mathrm{d} P(\mathcal{F})=0\).
(b)令\(\mathcal{F}\)和\(\mathcal{F}^{\prime}\)为分别对应于不同的联络\(\mathcal{A}\)和\(\mathcal{A}^{\prime}\)曲率2-形式. \(P(\mathcal{F^{\prime}})-P(\mathcal{F})\)的差是正合的.
| |
| 示性类(characteristic class) | 不变多项式是封闭的, 并且通常是不平凡的. 因此, 它定义了\(M\)的上同调类. 陈-Weil定理(b)确保该同调类与所选的规范势无关. 这样定义的同调类称为示性类. 由不变多项式\(P\)定义的示性类由\(\chi_{E}(P)\)表示, 其中\(E\)是定义联络和曲率的纤维丛. | |
| Weil同态(Weil homomorphism) | 令\(P\)是\(I^{*}(G)\)中的不变多项式, \(E\)是在\(M\)上具有结构群\(G\)的纤维丛,
(a)\(P\to \chi_{E}(P)\)映射\(P\to \chi_{E}(P)\)
\[\chi_{E}: I^{*}(G) \rightarrow H^{*}(M)\]
是一个同态(Weil同态).
(b)令\(f: N\to M\)为可微映射. 对于\(E\)的拖回丛\(f^{*}E\), 我们有naturality
\[\chi_{f^{*} E}=f^{*} \chi_{E}\].
| |
| Chern类(Chern class) | 令\(E \stackrel{\pi}{\longrightarrow} M\)为复向量丛, 其纤维为\(\mathbb{C}^{k}\). 结构群\(G\)是\(\mathrm{GL}(k,\mathbb{C})\)的子群, 并且规范势\(\mathcal{A}\)和场强\(\mathcal{F}\)在\(\mathfrak{g}\)取值. 定义总Chern类:
\[c(\mathcal{F}) \equiv \operatorname{det}\left(I+\frac{\mathrm{i} \mathcal{F}}{2 \pi}\right)\]
因为\(\mathcal{F}\)是2-形式, \(c(\mathcal{F})\)是偶数形式的直接求和
\[c(\mathcal{F})=1+c_{1}(\mathcal{F})+c_{2}(\mathcal{F})+\cdots\]
其中\(c_{j}(\mathcal{F}) \in \Omega^{2 j}(M)\)被称为\(j\)阶陈类.
| |
| 分裂原理(splitting principle) | 令\(E\)是\(n\)复线丛的Whitney和,
\[E=L_{1} \oplus L_{2} \oplus \cdots \oplus L_{n}\].
利用\(c(E \oplus F)=c(E) \wedge c(F)\), 有
\[c\left(L_{i}\right)=1+c_{1}\left(L_{i}\right) \equiv 1+x_{i}\]
因此
\[c(E)=\prod_{i=1}^{n}\left(1+x_{i}\right)\].
\(n\)-维向量丛\(E\)的Chern类与\(n\)个复线丛的Whitney和的类相同. 这被称为分裂原理.
| |
| 万有丛(universal bundles) | | |
| 分类空间(classifying space) | | |
| Chern特征标(Chern character) | 总Chern特征标定义为
\[\operatorname{ch}(\mathcal{F}) \equiv \operatorname{tr} \exp \left(\frac{\mathrm{i} \mathcal{F}}{2 \pi}\right)=\sum_{j=1} \frac{1}{j !} \operatorname{tr}\left(\frac{\mathrm{i} \mathcal{F}}{2 \pi}\right)^{j}\]
\(j\)阶Chern特征标\(\operatorname{ch}_{j}(\mathcal{F})\)定义为
\[\operatorname{ch}_{j}(\mathcal{F}) \equiv \frac{1}{j !} \operatorname{tr}\left(\frac{\mathrm{i} \mathcal{F}}{2 \pi}\right)^{j}\].
| |
| Todd类(Todd class) | 复向量丛对应的另一个有用的示性类——Todd类定义为
\[\operatorname{Td}(\mathcal{F})=\prod_{j} \frac{x_{j}}{1-\mathrm{e}^{-x_{j}}}\]
其中已经包括了分裂原理. 如果用\(x_{j}\)的幂次展开
\[\begin{aligned}
\operatorname{Td}(\mathcal{F}) &=\prod_{j}\left(1+\frac{1}{2} x_{j}+\sum_{k \geq 1}(-1)^{k-1} \frac{B_{k}}{(2 k) !} x_{j}^{2 k}\right) \\
&=1+\frac{1}{2} \sum_{j} x_{j}+\frac{1}{12} \sum_{j} x_{j}^{2}+\frac{1}{4} \sum_{ j < k } x_{j} x_{k}+\cdots \\
&=1+\frac{1}{2} c_{1}(\mathcal{F})+\frac{1}{12}\left[c_{1}(\mathcal{F})^{2}+c_{2}(\mathcal{F})\right]+\cdots
\end{aligned}\]
其中\(B_{k}\)是Bernoulli数
\[B_{1}=\frac{1}{6} \quad B_{2}=\frac{1}{30} \quad B_{3}=\frac{1}{42} \quad B_{4}=\frac{1}{30} \quad B_{5}=\frac{5}{66} \ldots \]
| |
| Pontrjagin类(Pontrjagin class) | 总Pontrjagin类定义为
\[p(\mathcal{F}) \equiv \operatorname{det}\left(I+\frac{\mathcal{F}}{2 \pi}\right).\]
\(p(\mathcal{F})\)的生成函数为
\[p(\mathcal{F})=\operatorname{det}(I+A)=\prod_{i=1}^{[k / 2]}\left(1+x_{i}^{2}\right), \qquad [k / 2]=\rightarrow\left\{\begin{array}{ll}
k / 2 & \text { if } k \text { is even } \\
(k-1) / 2 & \text { if } k \text { is odd. }
\end{array}\right.\]
每个Pontrjain类为
\[p_{j}(\mathcal{F})=\sum_{i_{1} < i_{2} < \ldots < i_{j} }^{[k / 2]} x_{i_{1}}^{2} x_{i_{2}}^{2} \ldots x_{i_{j}}^{2}.\]
| |
| 普法夫型(Pfaffian) | 一般地, \(2l\times 2l\)斜对称矩阵\(A\)的行列式是多项式Pfaffian \(\operatorname{Pf}(A)\)的平方
\[\operatorname{det} A=\operatorname{Pf}(A)^{2}\]
| Euler类(Euler class)\(M\)的Euler类\(e\)由4\(l\)-形式\(p_{l}\)的开方根定义为
\[e(A) e(A)=p_{l}(A)\] |
| Chern-Simons形式(Chern-Simons form) | 令\(P_{j}(\mathcal{F})\)是任意\(2j\)-形式的示性类. 因为\(P_{j}(\mathcal{F})\)是闭的, 通过Poincare引理局域地写成正合形式
\[P_{j}(\mathcal{F})=\mathrm{d} Q_{2 j-1}(\mathcal{A}, \mathcal{F})\]
其中\(Q_{2 j-1}(\mathcal{A}, \mathcal{F}) \in \mathfrak{g} \otimes \Omega^{2 j-1}(M)\). 该\(2j-1\)形式\(Q_{2 j-1}(\mathcal{A}, \mathcal{F})\)称为\(P_{j}(\mathcal{F})\)的Chern-Simons形式.
| Chern特征标\(\operatorname{ch}_{j}(\mathcal{F})\)的Chern-Simons形式
\[Q_{2 j-1}(\mathcal{A}, \mathcal{F})=\frac{1}{(j-1) !}\left(\frac{\mathrm{i}}{2 \pi}\right)^{j} \int_{0}^{1} \mathrm{~d}t\ \operatorname{str}\left(\mathcal{A}, \mathcal{F}_{t}^{j-1}\right)\]
例如
\[\begin{aligned}
Q_{1}(\mathcal{A}, \mathcal{F}) &=\frac{\mathrm{i}}{2 \pi} \int_{0}^{1} \mathrm{~d} t \operatorname{tr} \mathcal{A}=\frac{\mathrm{i}}{2 \pi} \operatorname{tr} \mathcal{A} \\
Q_{3}(\mathcal{A}, \mathcal{F}) &=\left(\frac{\mathrm{i}}{2 \pi}\right)^{2} \int_{0}^{1} \mathrm{~d} t \operatorname{str}\left(\mathcal{A}, t \mathrm{~d} \mathcal{A}+t^{2} \mathcal{A}^{2}\right) \\
&=\frac{1}{2}\left(\frac{\mathrm{i}}{2 \pi}\right)^{2} \operatorname{tr}\left(\mathcal{A} \mathrm{d} \mathcal{A}+\frac{2}{3} \mathcal{A}^{3}\right) . \\
Q_{5}(\mathcal{A}, \mathcal{F}) &=\frac{1}{2}\left(\frac{\mathrm{i}}{2 \pi}\right)^{3} \int_{0}^{1} \mathrm{~d} t \operatorname{str}\left[\mathcal{A},\left(t \mathrm{~d} \mathcal{A}+t^{2} \mathcal{A}^{2}\right)^{2}\right] \\
&=\frac{1}{6}\left(\frac{\mathrm{i}}{2 \pi}\right)^{3} \operatorname{tr}\left[\mathcal{A}(\mathrm{d} \mathcal{A})^{2}+\frac{3}{2} \mathcal{A}^{3} \mathrm{~d} \mathcal{A}+\frac{3}{5} \mathcal{A}^{5}\right]
\end{aligned}\]
|
| 同伦算子(homotopy operator) | 对于\(\mathcal{A}\)和\(\mathcal{F}\)的任何多项式\(S(\mathcal{A}, \mathcal{F})\), 得到
\[\left(\mathrm{d} l_{t}+l_{t} \mathrm{~d}\right) S\left(\mathcal{A}_{t}, \mathcal{F}_{t}\right)=\delta t \frac{\partial}{\partial t} S\left(\mathcal{A}_{t}, \mathcal{F}_{t}\right)\].
在\([0,1]\)上积分, 得到Cartan的同伦公式
\[S\left(\mathcal{A}_{1}, \mathcal{F}_{1}\right)-S\left(\mathcal{A}_{0}, \mathcal{F}_{0}\right)=\left(\mathrm{d} k_{01}+k_{01} \mathrm{~d}\right) S\left(\mathcal{A}_{t}, \mathcal{F}_{t}\right)\]
其中同伦算符\(k_{01}\)定义为
\[k_{01} S\left(\mathcal{A}_{t}, \mathcal{F}_{t}\right) \equiv \int_{0}^{1} \delta t\ l_{t} S\left(\mathcal{A}_{t}, \mathcal{F}_{t}\right)\]
| |
| Cech上同调群(Cech cohomology group) | 令\(\mathbb{Z}_{2}\)为乘法群\(\{-1, +1\}\). Cech \(r\)-上链是在\(U_{i_{0}} \cap U_{i_{1}} \cap \ldots \cap U_{i_{r}} \neq \emptyset\)上定义的函数\(f\left(i_{0}, i_{1}, \ldots, i_{r}\right) \in \mathbb{Z}_{2}\), 在任意排列\(P\)下完全对称,
\[f\left(i_{P(0)}, \ldots, i_{P(r)}\right)=f\left(i_{0}, \ldots, i_{r}\right).\]
令\(C^{r}\left(M, \mathbb{Z}_{2}\right)\)为Cech \(r\)-上链的乘法群. 我们定义上边界算符\(\delta: C^{r}\left(M ; \mathbb{Z}_{2}\right) \rightarrow C^{r+1}\left(M ; \mathbb{Z}_{2}\right)\)
\[(\delta f)\left(i_{0}, \ldots, i_{r+1}\right)=\prod_{j=0}^{r+1} f\left(i_{0}, \ldots, \hat{i}_{j}, \ldots, i_{r+1}\right)\]
其中省略了\(\hat{}\)以下的变量. 可以证明, 对于任何Cech \(r\)-上链 \(f\), 有\
\[\delta^{2} f=1.\]
上闭链群\(Z^{r}\left(M ; \mathbb{Z}_{2}\right)\)和上边界群\(B^{r}\left(M ; \mathbb{Z}_{2}\right)\)定义为
\[Z^{r}\left(M ; \mathbb{Z}_{2}\right)=\left\{f \in C^{r}\left(M ; \mathbb{Z}_{2}\right) \mid \delta f=1\right\}\]
\[B^{r}\left(M ; \mathbb{Z}_{2}\right)=\left\{f \in C^{r}\left(M ; \mathbb{Z}_{2}\right) \mid f=\delta f^{\prime}, f^{\prime} \in C^{r-1}\left(M ; \mathbb{Z}_{2}\right)\right.\]
将\(r\)阶Cech上同调群\(H^{r}\left(M ; \mathbb{Z}_{2}\right)\)定义为
\[H^{r}\left(M ; \mathbb{Z}_{2}\right)=\operatorname{ker} \delta_{r} / \mathrm{im} \delta_{r-1}=Z^{r}\left(M ; \mathbb{Z}_{2}\right) / B^{r}\left(M ; \mathbb{Z}_{2}\right).\]
| |
| Stiefel-Whitney类(Stiefel-Whitney class) | Stiefel-Whitney类\(w_{r}\)是一个示性类, 在\(H^{r}(M;\mathbb{Z}_{2})\)中取值. | 第一Stiefel-Whitney类\(w_{1}(M) \equiv[f] \in H^{1}\left(M ; \mathbb{Z}_{2}\right)\), 是可定向性的障碍(obstruction to the orientability)
第二Stiefel-Whitney类\(w_{2}(M) \in H^{2}\left(M, \mathbb{Z}_{2}\right)\)
|







 可交换
可交换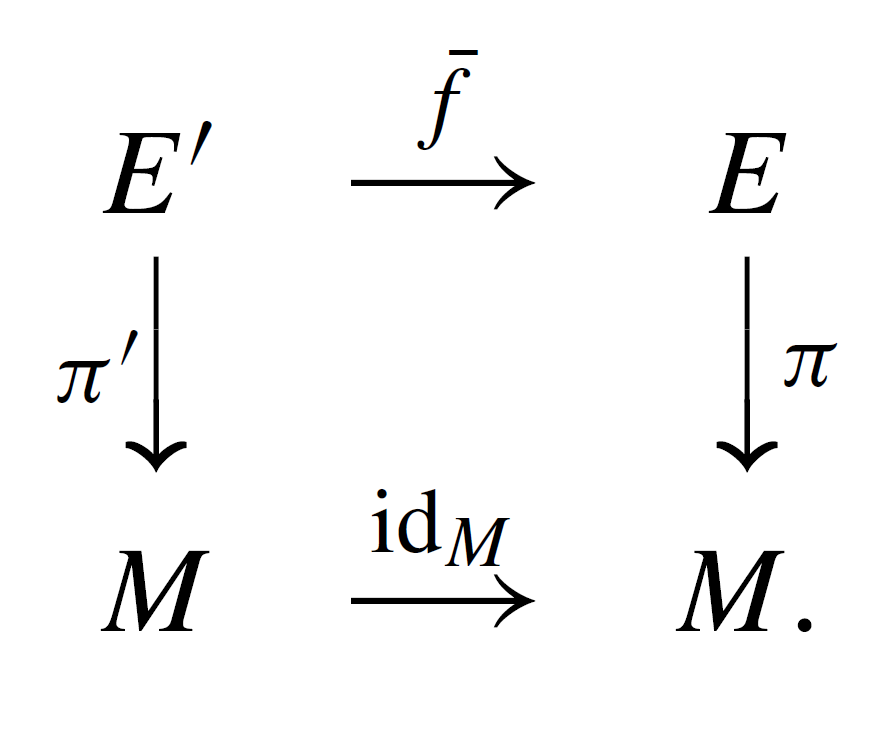
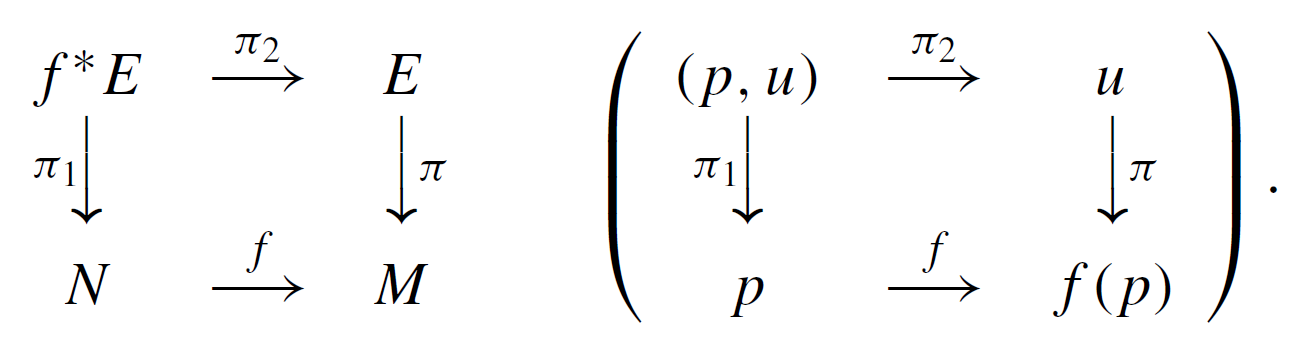
 因此, \(E \oplus E^{\prime}=\left\{\left(u, u^{\prime}\right) \in E \times E^{\prime} \mid \pi \times \pi^{\prime}\left(u, u^{\prime}\right)=(p, p)\right\}\). Whitney和丛的纤维是\(F \oplus F^{\prime}\).
因此, \(E \oplus E^{\prime}=\left\{\left(u, u^{\prime}\right) \in E \times E^{\prime} \mid \pi \times \pi^{\prime}\left(u, u^{\prime}\right)=(p, p)\right\}\). Whitney和丛的纤维是\(F \oplus F^{\prime}\).
