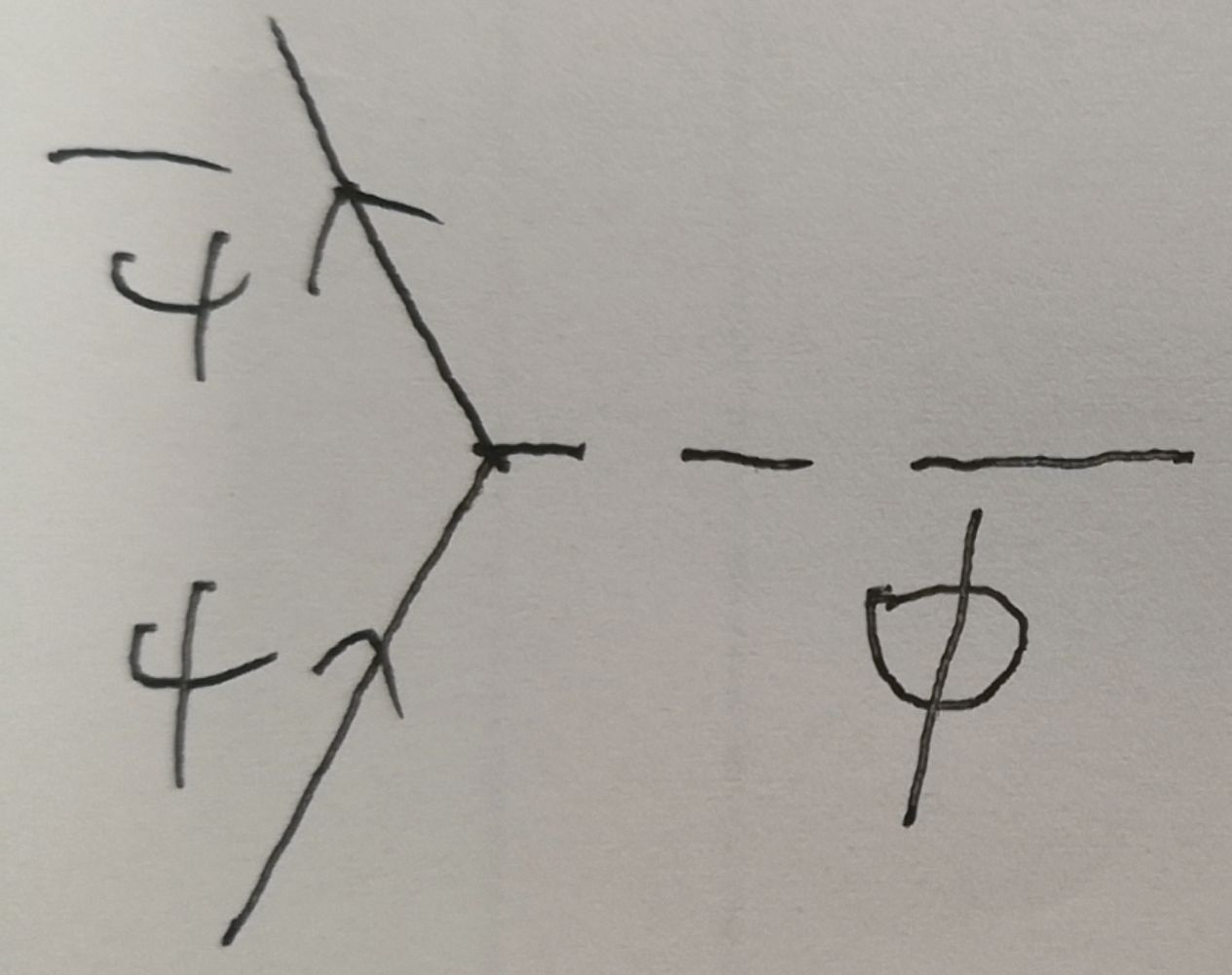返回上级菜单
3.28 周一
- 上节课图像补充:
1D Ising model重整化图像:

2D Ising model重整化图像,下图中\(K_c=\sqrt{2}-1\),说明2D系统存在相变,低温下铁磁有序,和零温物理一致;高温下铁磁无序,和\(+\infty\)温物理一致
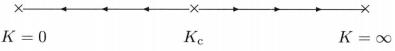
- 对费曼图做高阶修正:
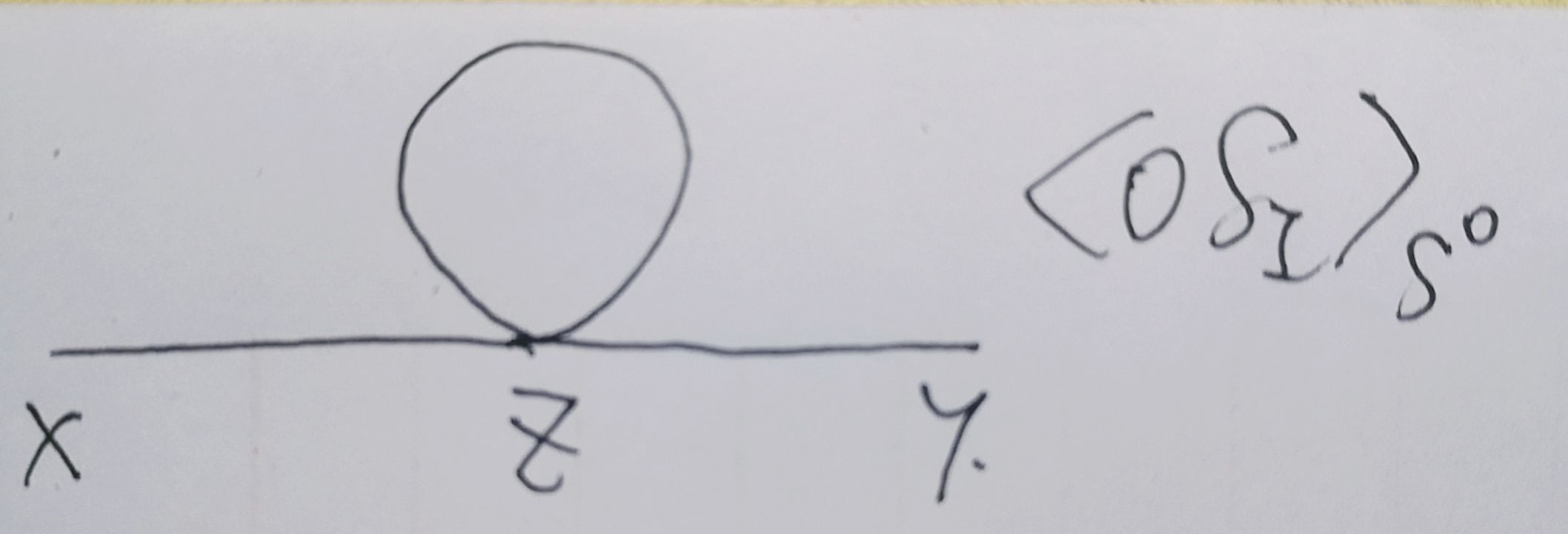 \(=\sum_k\frac{1}{k^2+m^2}=\frac{1}{(2\pi)^d}\int d^dk\frac{1}{k^2+m^2}=\frac{\Omega_d}{(2\pi)^d}\int_{b\wedge}^{\wedge}\frac{k^{d-1}dk}{k^2+m^2}\)
\(=\sum_k\frac{1}{k^2+m^2}=\frac{1}{(2\pi)^d}\int d^dk\frac{1}{k^2+m^2}=\frac{\Omega_d}{(2\pi)^d}\int_{b\wedge}^{\wedge}\frac{k^{d-1}dk}{k^2+m^2}\)
定义\(S_d=\frac{\Omega_d}{(2\pi)^d}\),做二阶近似得
原式\(=S_d\int_{b\wedge}^{\wedge}\frac{k^{d-1}}{k^2}(1-\frac{m^2}{k^2})dk=\wedge^{d-2}(1-b)-m^2\wedge^{d-4}(1-b)\)
 \(\propto\sum_q\frac{1}{q^2+m^2}\frac{1}{(q+k)^2+m^2}\simeq S_d\wedge^{d-4}(1-b)\)
\(\propto\sum_q\frac{1}{q^2+m^2}\frac{1}{(q+k)^2+m^2}\simeq S_d\wedge^{d-4}(1-b)\)
- 一阶微扰正比于相互作用耦合系数,二阶微扰一定降低基态能量
\(H=H_0+V,E_n=E_n^0+\lambda V_{nn}-\lambda^2\sum_{m\neq n}\frac{|V_{mn}^2|}{E_m^0-E_n^0}\)
故BCS理论中有效电子电子配对给出的是吸引相互作用,大致论证如下:
固体材料中电子声子相互作用一阶项如下图片所示
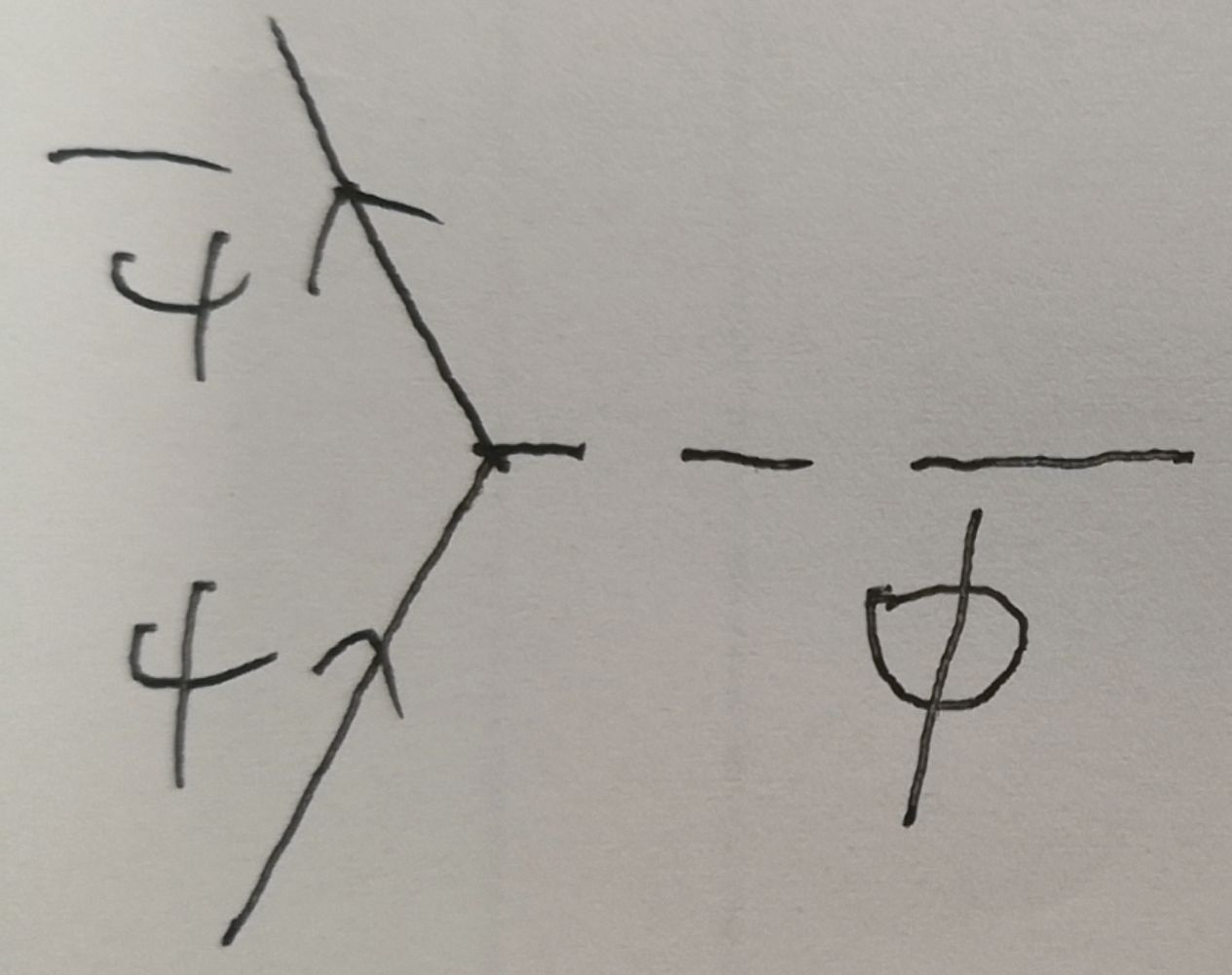
电子声子相互作用二阶项给出BCS理论中有效电子电子相互作用,为电子和电子通过传递声子配对,该相互作用是二阶微扰降低基态能量,故为吸引相互作用
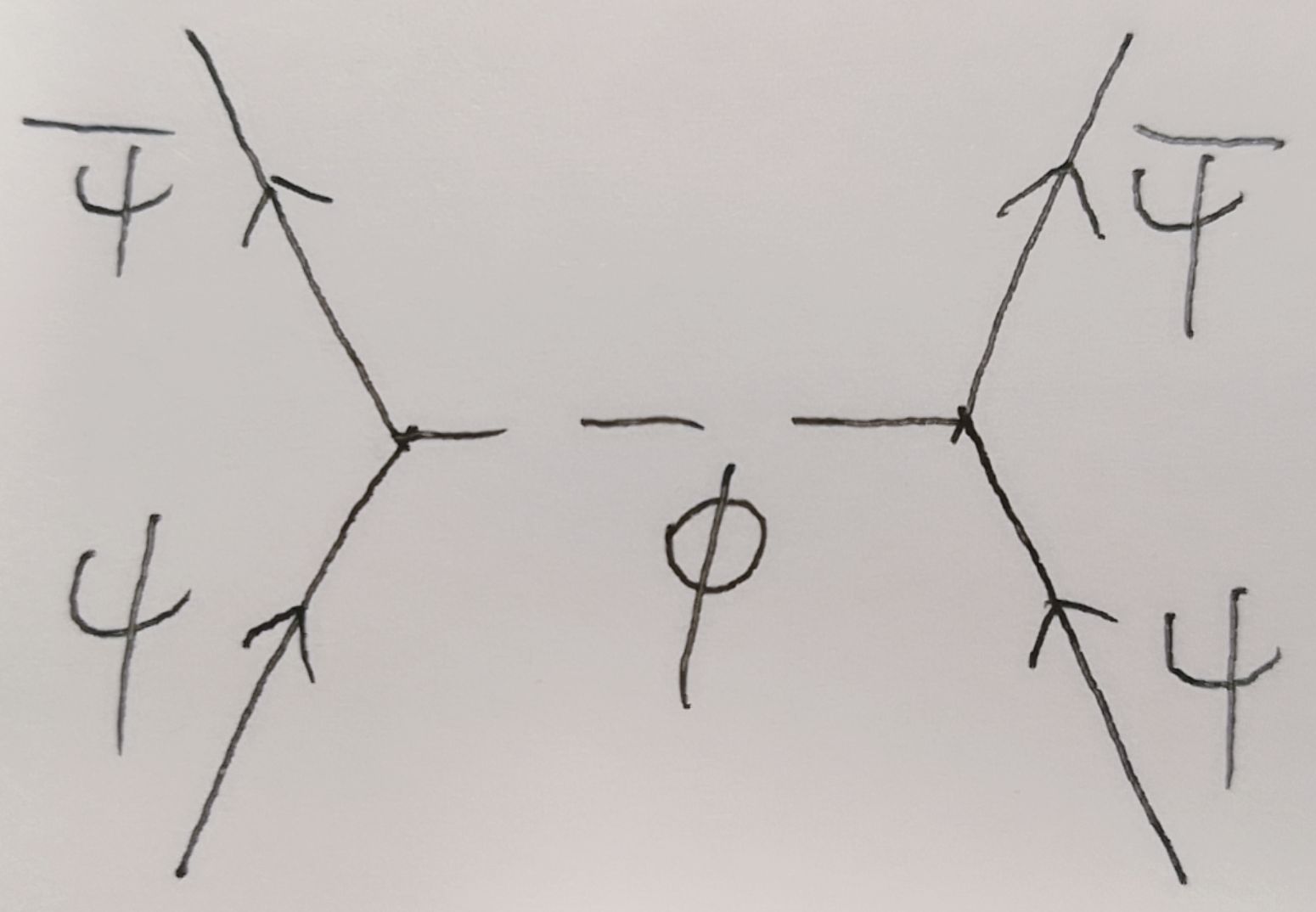
真实电子电子有效相互作用包括:库伦排斥、二阶微扰吸引项、\(2n+2\)阶微扰项。一般情况下二阶微扰吸引项大于库伦排斥项,BCS理论下电子和电子间为吸引相互作用。四阶项费曼图如下所示:

其他应用:Yang-Mills理论、Sidney-Coleman-Wilzeck工作
- Rescaling:\(\int D\phi_{\langle}e^{-S_{eff}},S_{eff}=\sum_{|k|\leq b\wedge}\phi_{k_1}\phi_{k_2}\phi_{k_3}\phi_{k_4}\delta(k_1+k_2+k_3+k_4)\)
Renormalization前\(|k|\leq\wedge\),Renormalization后\(|k|\leq b\wedge\)。Rescaling前\(|k|\leq b\wedge\),Rescaling后\(|k|\leq\wedge\)
在动量空间中,Rescaling本质上是标度变换,将\(b\wedge\)的物理再标度变换到\(\wedge\),相当于一根橡皮筋伸长后剪掉一部分再伸长再剪掉一部分\(\cdot\cdot\cdot\),参考我写的Note
设\(k=bq\),\(\phi_k=Z\phi_q\),根据\(\sum_k\frac{k^2}{2}\phi_k^*\phi_k\rightarrow\frac{1}{(2\pi)^d}\int_{|k|\leq b\wedge}dk\frac{k^2}{2}\phi_k^*\phi_k=\frac{1}{(2\pi)^d}b^{d+2}Z^2\int_{|q|\leq\wedge}dq\frac{q^2}{2}\phi_q^*\phi_q\)
于是有\(b^{d+2}Z^2=1\rightarrow Z=b^{-1-d/2}\),对于动量空间中未做标度变换下只积分掉高能球壳给出(参考上节课内容)\(m^2\rightarrow m^2+\frac{\lambda}{2}\Omega_d\wedge^{d-2}(1-b)\)
在标度变换(Rescaling)后\(m^2\int_{|k|\leq b\wedge}dk\phi_k^*\phi_k=m'^2b^dZ^2\int_{|q|\leq\wedge}dq\phi_q^*\phi_q=m'^2b^{-2}\int_{|q|\leq\wedge}dq\phi_q^*\phi_q\)
于是得到标度变换后质量\(m^2=m'^2b^{-2}\),或者可以这样理解:当从\(|k|\leq\wedge\)标度变换到\(|k|\leq b\wedge\)后\(m^2\rightarrow m^2b^{-2}\)
故同时考虑Renormalization和Rescaling后,即将\(b\wedge\leq|k|\leq\wedge\)积分掉过后剩余部分再\(b\wedge\rightarrow\wedge\),后质量变换公式:
\(m_1^2(m_0^2,b)=b^{-2}[m_0^2+\frac{\lambda}{2}\Omega_d\wedge^{d-2}(1-b)]\)
类似的,相互作用系数\(\lambda\)经过Renormalization和Rescaling后,相互作用系数变为
\(\lambda_1(\lambda_0,b)=b^{d-4}[\lambda-B\lambda^2S_d\wedge^{d-4}(1-b)]\)
\(\beta -function\):取\(b=1-dl\),定义\(\beta(\lambda)=\frac{d\lambda}{dl}=B\lambda^2\wedge^{d-4}+(d-4)\lambda\)
其中重整化流如下图所示。而\(\lambda\langle 0\)是非物理的部分,因为一阶微扰下能量趋近于负无穷,相当于每多一个粒子能量越来越趋近于负无穷,便不存在基态了。或者可以这样理解:\(m^2\phi^2(x)+\lambda\phi^4(x)\)画出能量随着\(\langle\phi\rangle\)的变化曲线,发现不存在能量最低点
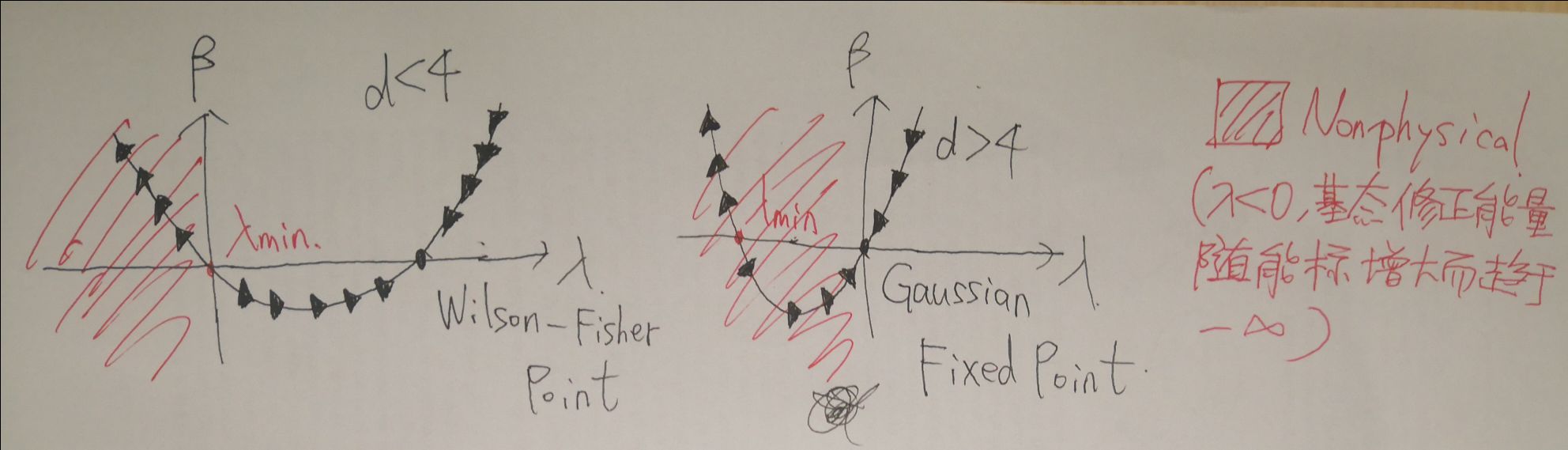
重整化流绘制方法:\(m_0^2\rightarrow m_1^2=m_1^2(m_0^2,b)\rightarrow m_2^2=m_2^2(m_1^2,b)\rightarrow\cdot\cdot\cdot,\lambda_0\rightarrow\lambda_1=\lambda_1(\lambda_0,b)\rightarrow\lambda_2=\lambda_2(\lambda_1,b)\rightarrow\cdot\cdot\cdot\)
微扰到二阶项后重整化流构型如下图所示:
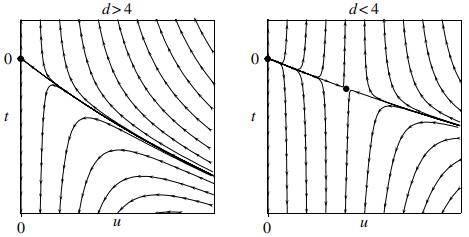
\(\lambda>0\),在\(m^2=0\)处有相变;当\(m^2\langle 0\)时候,基态\(\langle\phi\rangle\neq0\),当\(m^2\rangle 0\)时,基态\(\langle\phi\rangle=0\),发生自发对称破缺相变
- 作业3:用C语言或Matlab或Mathematica或Python等语言绘制\(m^2\)-\(\lambda\)重整化流,自己选参数 :
图像大致长相:Shankar书245页Fig13.4,Shankar书238页图像,但是Shankar书重整化公式用的是
\(S=\int_0^{\wedge}\phi^*(k)k^2\phi(k)\frac{d^dk}{(2\pi)^d}+r_0\int_0^{\wedge}\phi^*(k)\phi(k)\frac{d^dk}{(2\pi)^d}+\frac{u_0}{4}\int_{|k|<\wedge}\phi^*(-k_1-k_2-k_3)\phi^*(k_3)\phi(k_2)\phi(k_1)\prod_{i=1}^3\frac{d^dk_i}{(2\pi)^d}=S_0+S_I\)
请在做题时采用Peskin公式\(L=\frac{1}{2}(\partial\phi)^2-\frac{m^2}{2}\phi^2-\frac{\lambda}{4!}\phi^4\),并给出Wilson-Fisher Point的理论值和模拟值
请绘制出\(d>4,d<4,d=4\)的三张重整化流出来,横坐标纵坐标为\(m^2,\lambda\),需要取多个初始值画出多条线看大致走势,逐渐逼近边界但不需要画出边界(因为实际公式是近似的),并求出Wilson Fixed Point值,自己画图模拟值和理论值是否有偏差(因为公式本身是近似,所以可能有偏差,请说明以下偏离了多少)
参考方法:shankar13-14章,kardar,chap5,重整化流大致长相:kardar,chap5,Fig5.5
- 作业4:题目二选一
学生笔记
学生笔记2
3.31 周四
- 本节内容参考:
- Lectures on bosonization,C.L.Kane
- Fermions in one-dimension:Tomonaga-Luttinger Liquid,Sachdev
- shankar17-19章
- An introduction to bosonization,senechal
- Cazalilla,bosonization one-dimensional cold atom gases
- Introduction to one dimensional physics and luttinger liquid
- 诺贝尔奖Haldane,1979-1981年间论文,包括:
- 论文1
- 论文2
- 区分概念:Regularization正规化,Renormalization重整化,RenormalizationGroup重整化群,Rescaling重新标度
RenormalizationGroup典型粒子为Ising Model对偶数格点求迹,对Wilson积分掉动量空间的高能区域,Renormalization最典型粒子为2D\(\delta(x)\)势取发散截断求本正能量
重整化群一般为半群,以Ising Model对偶数格点求迹为例,\(K_{n+1}=R(K_n)\),半群是不可逆的
Rescaling为标度变换而已,在标度变换下\(k\rightarrow bk(b\rightarrow1^-),\lambda\rightarrow\lambda b^{d-4},m^2\rightarrow m^2b^{-2}\),如下图所示
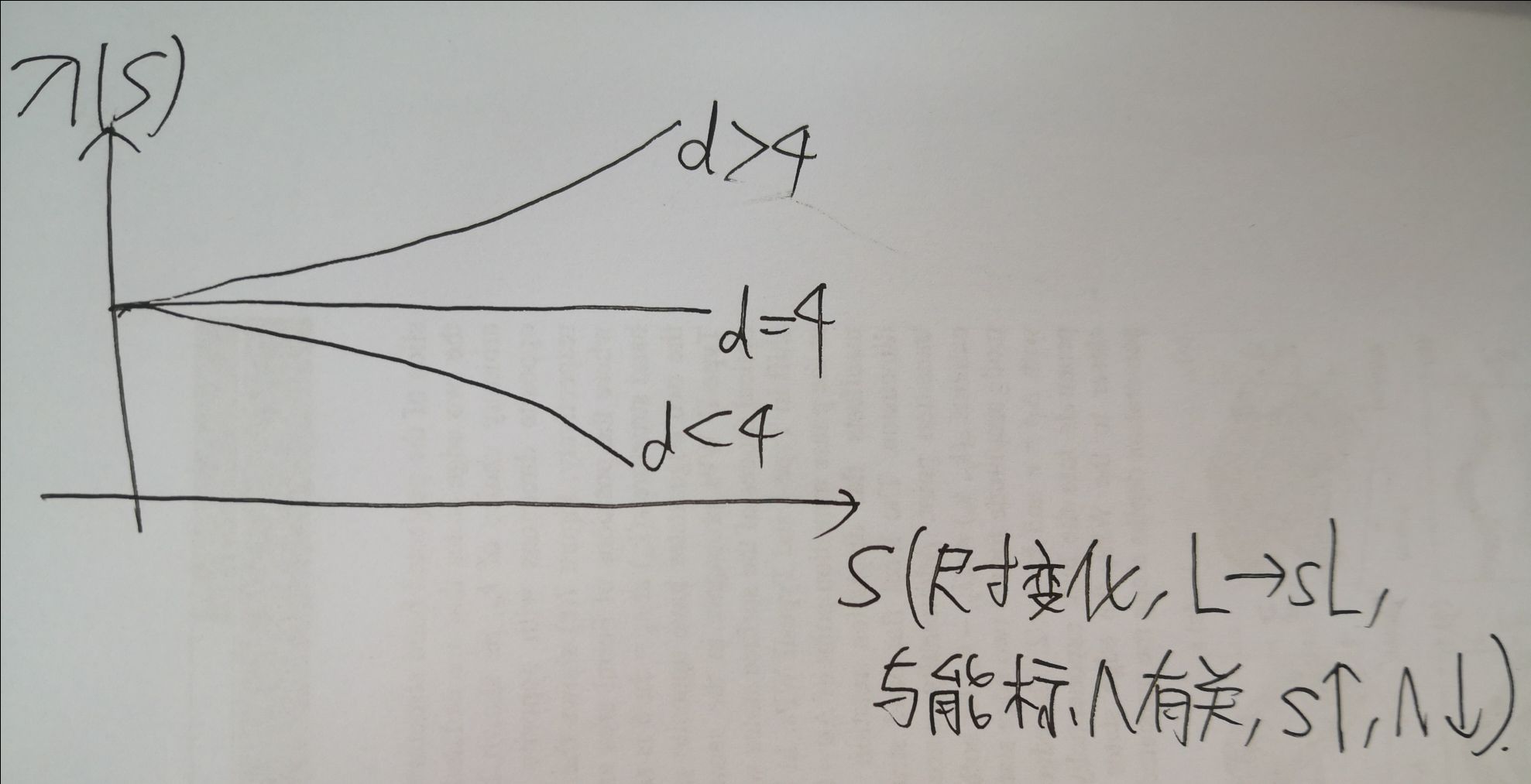
- 观测与能标的关系:
正规化-如何消除求和发散?回顾黎曼\(\zeta\)函数:\(1+\frac{1}{2}+\frac{1}{3}+\cdot\cdot\cdot=-\frac{1}{12}\),参考卡西米尔力,苗兵
观测到电荷\(e^*\)、质量\(m^2\)、耦合系数\(\lambda\)不是真实值,而是低能有效值
相变能标越高临界指数越接近真实结果
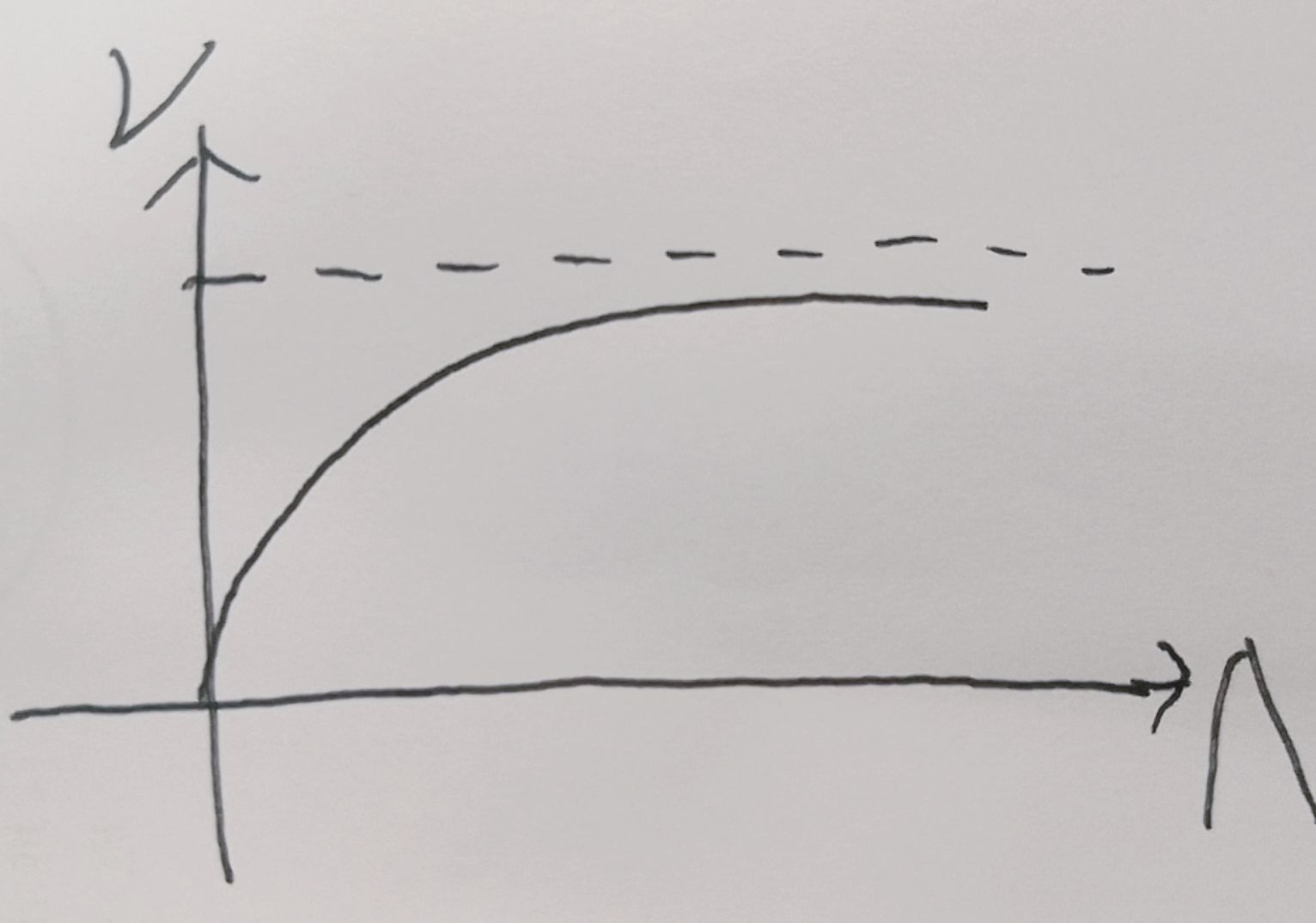
- Bosonization初步:简介对偶
实数空间和动量空间就是对偶
BKT相变和1D量子相变(Sine-Gordon Model)就是对偶。BKT相变见shankar18.1节,1D量子相变见shankar18.4节,作用量为
\(H_{BKT}=\frac{1}{2}[(\partial_x\phi)^2+(\partial_y\phi)^2]+Jcos\phi\)
\(L_{SG}=\frac{1}{2}[(\partial_t\phi)^2-(\partial_x\phi)^2]+Acos\phi\)
D维量子体系可与\(D+1\)维经典体系对偶。但是这里\(\phi\)是相位因子,而不是\(\phi^4\)理论的振幅因子
Sidney Coleman严格证明了Sine-Gordon Model(shankar18.4节)严格和Thirring Model(shankar18.1.2节)对偶
Application:Lots of physical systems(cold atom,1D superconductor,Hall Effect,et al)
\(d\leq3D\)在空间中交换两个粒子有费米子/玻色子,\(d=2D\)有任意子,\(d=1D\)有任意子,但是无法做交换做编制,只会有密度和相位改变,不同统计都对应着玻色激发
- 额外补充:Mermin-Wagner Theorem:1D、2D系统无长程序,3D系统有长程序,也就是说1D系统在考虑声子激发后不存在完美晶体,1D、2D系统在考虑海森堡模型磁激发后不存在完美晶体
1D声子系统:\(N=\sum_q\frac{1}{e^{\beta H(q)}-1}\sim\int dq\frac{1}{e^{\beta vq}-1}\),是发散的
2D磁性系统:Heisenberg Equation,\(H=-J\sum_{\langle ij\rangle}\vec{S}_i\cdot\vec{S}_j=-J\sum_{\langle ij\rangle}cos\theta_{ij}\),类似固体物理中完全有序晶格基态中激发声子,在基态上激发磁子,
在小角近似下\(H=\int d^2x\frac{J}{2}(\triangledown\theta)^2\),能量激发曲线为\(\epsilon(q)=vq^2\),\(N=\sum_q\frac{1}{e^{\beta \epsilon(q)}-1}\sim qdq\frac{1}{e^{\beta vq^2}-1}\)是发散的
- 从Kane Note出发推导玻色化,参考:Lectures on bosonization,C.L.Kane
1D chain中声子激发:\(k_F=\pm\pi\)附近出现激发,\(\omega=v|q|\),\(q=n\pi/L,\omega_q=\frac{\pi v}{L}n\rightarrow H=\frac{v\pi}{L}\sum_{n\leq1}nb_n^{\dagger}b_n\)
在推导此哈密顿量中隐含了一种对偶思想,费米子算符本来是反对易关系的\(\psi(r)\),我们用满足对易关系的Bose型算符\(\theta_i\)(\(r_i=r_i^0+\frac{a}{\pi}\theta_i\))来代替费米算符,结果该哈密顿量和声波、光波对偶,这是玻色化思想
Fermion体系:\(H=\int \psi^{\dagger}(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}-\mu)\psi,H=\sum_k(\frac{\hbar^2k^2}{2m}-\mu)\psi_k^{\dagger}\psi_k\)
我们只需要得到\(k_F\)附近等效行为,参考:Shankar书Eq18.80-Eq18.83,推导如下:只取费米面附近小量\(\wedge\)截断
\(\psi(j)=\int_{-\pi}^{\pi}\psi(k)e^{ikj}\frac{dk}{2\pi}\simeq\int_{-\wedge}^{\wedge}\psi(K_F+k)e^{iK_Fj}e^{ikj}\frac{dk}{2\pi}+\int_{-\wedge}^{\wedge}\psi(-K_F+k)e^{-iK_Fj}e^{ikj}\frac{dk}{2\pi}\)
定义\(\psi(K_F+k)=\psi_+(k),\psi(-K_F+k)=\psi_-(k)\),有
\(\psi(j)=\int_{-\wedge}^{\wedge}\psi_+(k)e^{iK_Fj}e^{ikj}\frac{dk}{2\pi}+\int_{-\wedge}^{\wedge}\psi_-(k)e^{-iK_Fj}e^{ikj}\frac{dk}{2\pi}\)
做变换\(\int_{\wedge}^{\wedge}\rightarrow\int_{-\pi}^{\pi}\),并傅里叶变换得
\(\psi(j)=\sqrt{a}[e^{iK_Fj}\psi_+(x=aj)+e^{-iK_Fj}\psi_-(x=aj)]=e^{iK_Fx}\psi_R(x)+e^{-iK_Fx}\psi_L(x)\)
由于\(\psi_{R/L}(x)=\int_{-\wedge}^{\wedge}\psi(\pm K_F+k)e^{ikx}\frac{dk}{2\pi}\),故\(\psi_{R/L}\)由一系列k较低波包构成,是慢变场,即波函数随在x方向上振动较慢,\(e^{\pm iK_Fx}\)是快变场,波函数在x方向上振动较快
求解哈密顿量\(H=\int dx[e^{-iK_Fx}\psi_R^{\dagger}+e^{iK_Fx}\psi_L^{\dagger}](-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}-\mu)[e^{iK_Fx}\psi_R+e^{-iK_Fx}\psi_L]\)
需要用到:\(\frac{\hbar^2}{2m}k_F^2=\mu\),以及忽略慢变场的二阶偏导\(\frac{d^2}{dx^2}\psi_{R/L}\)
并同时用到引理:\(\int dx\text{慢变包络}\cdot\text{正弦型快变波包}=0\),考察下图(\(\int dxf(x)=\int dxe^{-x^2}cos(100x)\))即可:
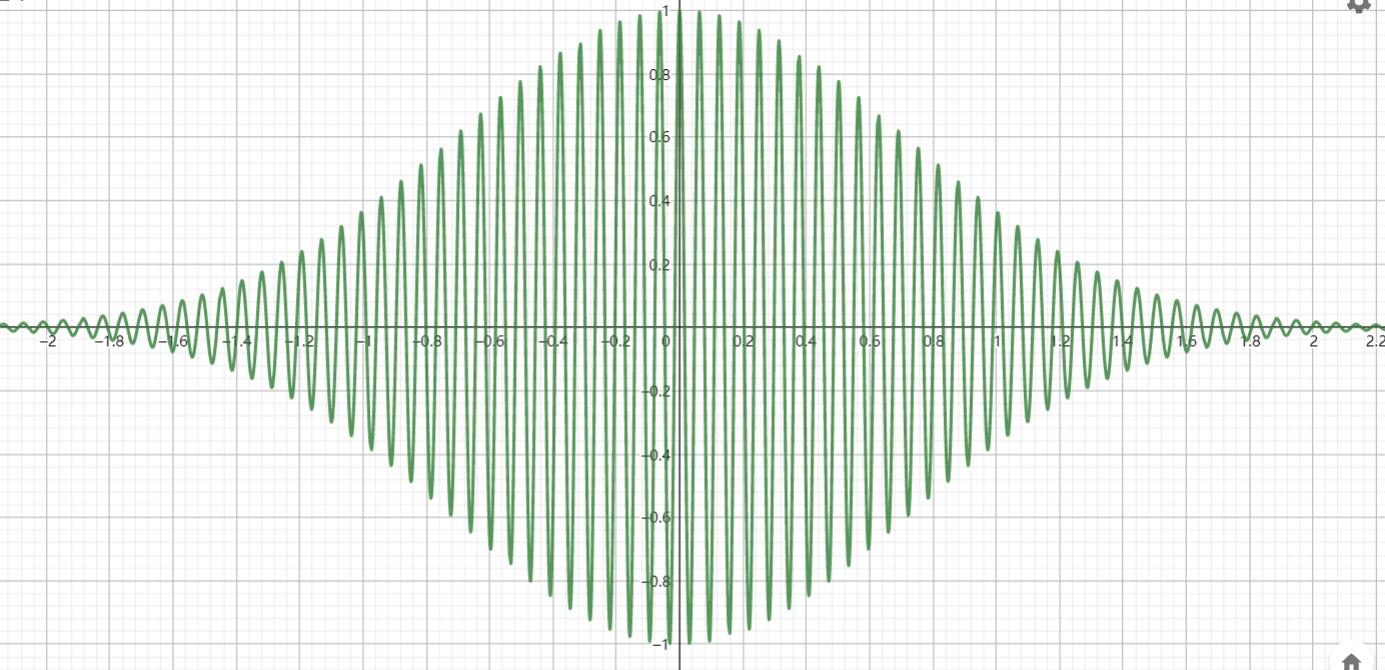
故最终结果为\(H=dx\hbar v_F\int \psi_R^{\dagger}(-i\frac{d}{dx})\psi_Rdx-v_F\psi_L^{\dagger}(-i\frac{d}{dx})\psi_L\)
下列引自Lectures on bosonization,C.L.Kane:
这种形式,1D在费米面附近的低能低动量长程激发,为Luttinger model
对称性:满足手征对称性\(\Gamma^{\dagger}H\Gamma=-H\),在固体物理两能带模型中手征对称性形式为\(\Gamma^{\dagger}H_k\Gamma=-H_k\)
除了total charge \(N_R+N_L\)外,还有个手征守恒荷\(N_R-N_L\)
- 费米子和玻色子在1D时可严格对偶,具体推导见Fermions in one-dimension:Tomonaga-Luttinger Liquid,Sachdev
- 作业5:推导Fermions in one-dimension:Tomonaga-Luttinger Liquid,Sachdev文献中Eq1-Eq11,并接着Eq1-Eq11式子往下推导彻底证明出费米玻色对偶关系\(Z_F=Z_B\)
要求:能尽可能详细的用自己的话阐明Eq1-Eq11每一个公式的物理意义,按照每一个物理意义给分,之后助教会评讲的
学生笔记
学生笔记2
4.2 周六
- 本节内容参考:
- jordan-wigner and bosonization
- Kapil Adhikari-Bosonization lecture
- shankar17-19章
- jordan-wigner transformation:In 1927,Jordan and Wigner established a mapping between fermion and spin-1/2 \(\sigma\) operators
上结论:\(\sigma_i^+=exp[i\pi\sum_{j=-\infty}^{i-1}c_j^{\dagger}c_j]c_i^{\dagger}=Uc_i^{\dagger}\),其中\(exp[i\pi\sum_{j=-\infty}^{i-1}c_j^{\dagger}c_j]\)项表示x点的粒子与\(-\infty\sim x-1\)的粒子有关,这是弦的性质
证明上面式子,需要证明两个公式,第一个公式:\(\sigma_i^-\sigma_i^++\sigma_i^+\sigma_i^-=I\),这个利用\(e^ABe^{-A}=B+[A,B]+\frac{1}{2}[A,[A,B]]+\cdot\cdot\cdot\)很好证明
还得证明的式子是\(\sigma_i^{\dagger}\sigma_{i'}^{\dagger}\),即\(U(i)c_i^{\dagger}U(i')c_{i'}^{\dagger}=U(i')c_{i'}^{\dagger}U(i)c_i^{\dagger}\)
我们假设\(i'\langle i\),有以下公式:
\(U(i)U(i')=U(i')U(i),U(i)c_i=c_iU(i),U(i')c_i^{\dagger}=c_i^{\dagger}U(i'),c_{i'}^{\dagger}U(i)=-U(i)c_{i'}^{\dagger}\)
故有\(c_i^{\dagger}U(i)c_{i'}^{\dagger}U(i')=c_{i'}^{\dagger}U(i')c_i^{\dagger}U(i)=c_{i'}^{\dagger}c_i^{\dagger}U(i')U(i)=-c_i^{\dagger}c_{i'}^{\dagger}U(i')U(i)=-c_i^{\dagger}c_{i'}^{\dagger}U(i)U(i')=c_i^{\dagger}U(i)c_{i'}^{\dagger}U(i')\)
类似的方法可证明费米玻色变换\(f^{\dagger}(x)=exp[\pm i\pi\int_{-\infty}^xn(x')dx']b^{\dagger}(x)\),以及任意子与玻色子变换,任意子对易关系为\(e^{i\theta}\psi_i\psi_j-\psi_j\psi_i=0\),故任意子玻色子变换为\(\psi_i^{\dagger}=exp[i\theta\sum_{u=1}^{i-1}b_u^{\dagger}b_u]b_i^{\dagger}\)
- 1D XX model:少数严格可解的Model,\(H=-J\sum_i(\sigma_i^x\sigma_{i+1}^x+\sigma_i^y\sigma_{i+1}^y+h\sigma_i^z)\),作Jordan-Wigner变换求解得
\(\sigma_i^+=exp[\sum_{j=0}^{i-1}i\pi c_j^{\dagger}c_j]c_i^{\dagger}\),\(\sigma_i^+\)的物理意义:类似量子光学中的原子从基态激发到了激发态\(\sigma_i^+=\sigma_x+i\sigma_y=|e\rangle\rangle g|\),类似的\(\sigma_i^-=|g\rangle\langle e|=\sigma_x-i\sigma_y,\sigma_z=\sigma_+\sigma_--\sigma_-\sigma_+\)
\(\sigma_i^z=2c_i^{\dagger}c_i-1\)
\(H=-\frac{J}{2}\sum_j(c_j^{\dagger}c_{j+1}+c_{j+1}^{\dagger}c_j)+\sum_jh(2c_j^{\dagger}c_j-1)=-J\sum_kcoskc_k^{\dagger}c_k+h\sum_k(2c_k^{\dagger}c_k-1)\)
其中磁场项起到了调节Fermi面的作用,在费米面附近做泰勒展开得\(\epsilon=\pm v|k|\)
加相互作用得到XXZ model,\(H=-J\sum_i(\sigma_i^x\sigma_{i+1}^x+\sigma_i^y\sigma_{i+1}^y-\triangle\sigma_i^z\sigma_{i+1}^z)\),可用Bethe ansatz严格求解,这里不展开论述
类似的道理,对XXZ model做Jordan-Wigner变换后\(H=-\frac{J}{2}(c_j^{\dagger}c_{j+1}+c_{j+1}^{\dagger}c_j)+\triangle\sum_j(n_j-\frac{1}{2})(n_{j+1}-\frac{1}{2})\)
- 什么样的相互作用能打开Gap?
不可能是\(\int\psi^{\dagger}(x)\psi^{\dagger}(x)dx\),因为等于0
联系超导配对:单分量对应p波配对能打开Gap
试着构造\(H=\frac{1}{2}\int dx\psi^{\dagger}(x)(-i\frac{\partial}{\partial x})\psi^{\dagger}(x)\),其中\(\psi=\frac{1}{\sqrt{2}}(e^{ik_Fx}\psi_R+e^{-ik_Fx}\psi_L)\),根据上节课描述的快变慢变等内容,有
\(H=\frac{k_F}{2}(\psi_R^{\dagger}\psi_L^{\dagger}-\psi_L^{\dagger}\psi_R^{\dagger})=k_F\psi_R^{\dagger}\psi_L^{\dagger}\)
第二种能打开Gap形式为对自由电子气的晶格势周期微扰,形式为\([-\frac{d^2}{dx^2}-\mu+Acos(2k_Fx)]\psi(x)=E\psi(x)\),能带大致如下所示
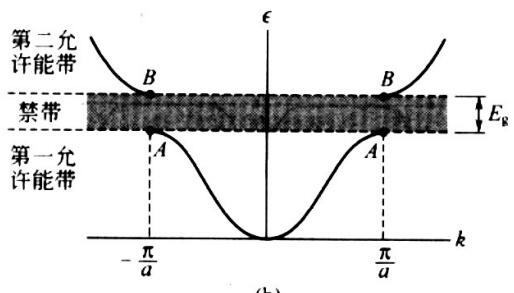
据上面公式可推出费米面附近电子发生散射能导致Gap,证明如下:
\(\int dxAcosx\psi^{\dagger}\psi=\int dxAcos(2k_Fx)[e^{-ik_Fx}\psi_R^{\dagger}+e^{ik_Fx}\psi_L^{\dagger}][e^{ik_Fx}\psi_R+e^{-ik_Fx}\psi_L]\)
上式中存在此项:\(\frac{1}{2}\int dxAcos(2k_Fx)[\psi_R^{\dagger}\psi_R+\psi_L^{\dagger}\psi_L]\),其中cosx是快变项,\(\psi_{L/R}\)是慢变项,根据上节课论述\(\int dx\cdot\text{快变项}\cdot\text{慢变项}=0\),故此项值为0
剩下两项为\(\frac{A}{2}\int dxcos(2k_Fx)[e^{-2ik_Fx}\psi_R^{\dagger}\psi_L+e^{2ik_Fx}\psi_L^{\dagger}\psi_R]\),再次应用上节课讲的引理\(\int dx\cdot\text{快变项}\cdot\text{慢变项}=0\)得
\(\int Acos(2k_Fx)\psi^{\dagger}\psi dx=\frac{A}{4}\int[\psi_L^{\dagger}\psi_R+\psi_R^{\dagger}\psi_L]dx\)
\[H_F=\begin{eqnarray}\left(\begin{array}{cccc}
vk &0\\ 0 &-vk\\
\end{array}\right)+\left(\begin{array}{cccc}
0 &g\\g &0\\
\end{array}\right)\end{eqnarray}\]
左边矩阵表示没有散射时候费米面附近左右两侧各自独立哈密顿量,右边矩阵为引入散射项,能量本征值\(E=\sqrt{v^2k^2+g^2}\),故散射一定打开Gap
可以用外场激发某些散射,从而导致相变。Gap打开\(\leftrightarrow\)导致相变
- Interacting Boson Model,原理参考文小刚书60-63页,在BEC凝聚体中加入相互作用后波函数变化为\(\varphi=\varphi_0+\delta\varphi\),其中\(\varphi_0\)为凝聚体,\(\delta\varphi\)为小激发
今天讲解新处理方法,玻色算符表示为\(b=e^{i\theta}\sqrt{n}\),其中对易关系为\([n(x),\theta(y)]=i\delta(x-y)\),具体推导见郭光灿《量子光学》1.8节,推至\([N,cos\phi]=-isin\phi,[N,sin\phi]=icos\phi\)这部分过后进行泰勒展开可得\([N,\phi]=i\)
我们将在\(n and\theta\)表象下处理,其中\(n=n_0+\rho\),其中\(n_0\)为BEC凝聚体大的密度,等价为大的湖,\(\rho\)为小的激发,等价为湖表面的振动

Interacting Boson体系的哈密顿量为\(H=\int dx\frac{\hbar^2}{2m}(\frac{d}{dx}\psi^{\dagger})(\frac{d}{dx}\psi)+g\int(\psi^{\dagger}\psi)^2dx\)
考虑\(n=n_0+\rho,\rho\langle\langle n_0\),哈密顿量变为
\(H=\int dx\frac{\hbar^2n_0}{2m}(\partial_x\theta)^2+\frac{(\partial_x\rho)^2}{8mn_0}+\int g(n_0+\rho)^2dx=const+\int dx\frac{\hbar^2n_0}{2m}(\partial_x\theta)^2+\int dx\frac{(\partial_x\rho)^2}{8mn_0}+g\int dx\rho^2\)
进行傅里叶变换\(\rho(x)=\frac{1}{\sqrt{L}}\sum_qe^{iq\cdot x}\rho_q\)可得
\(H=\frac{\hbar^2n_0}{2m}\sum_qq^2\theta_q\theta_{-q}+\sum_q\frac{\hbar^2}{8mn_0}q^2\rho_q\rho_{-q}+g\sum_q\rho_q\rho_{-q}=\sum_{q\rangle0}\frac{\hbar^2n_0q^2}{m}\theta_q^*\theta_q+\frac{\hbar^2}{4mn_0}q^2\rho_q\rho_{-q}+2g\rho_q^*\rho_q\),其中\([\rho_q,\theta_q^*]=i\)
类似谐振子\([x,p]=i\hbar,H=\frac{p^2}{2m}+\frac{m}{2}\omega^2x^2\),我们可以得到此的激发频率为\(\omega_p=\sqrt{\frac{p^2}{2m}(\frac{p^2}{2m}+2g\rho_0)}\)
可以看到,用\(\rho,\theta\)共轭表象比用\(\psi,\psi^{\dagger}\)共轭表象更能处理相互作用,还能处理强相互作用
关联函数具体求法(纯粹是我个人补充,不要求掌握),参考jordan-wigner and bosonization第6页和Lectures on bosonization,C.L.Kane
\(\langle0|\psi^{\dagger}(x)\psi(x')\rangle\sim\rho_0\langle0|e^{-i\theta(x)}e^{i\theta(x')}|0\rangle\)
根据前面论述的累积量展开公式,保留到二阶项得\(\langle0|\psi^{\dagger}(x)\psi(x')|0\rangle\sim\rho_0exp[-\frac{1}{2}\langle0|[\theta(x)-\theta(x')]|0\rangle]\)
只考虑低能激发,对玻色子体系\(\epsilon_p=vp\),则序参量为\(\int dq\frac{1-cosq|x-x'|}{e^{\beta vq}-1}\sim\frac{1}{|x-x'|}(|x-x'|\rightarrow+\infty)\),故1D相互作用体系无长程序
1D费米子激发声子体系:后续再慢慢讨论
学生笔记
学生笔记2
学生笔记3

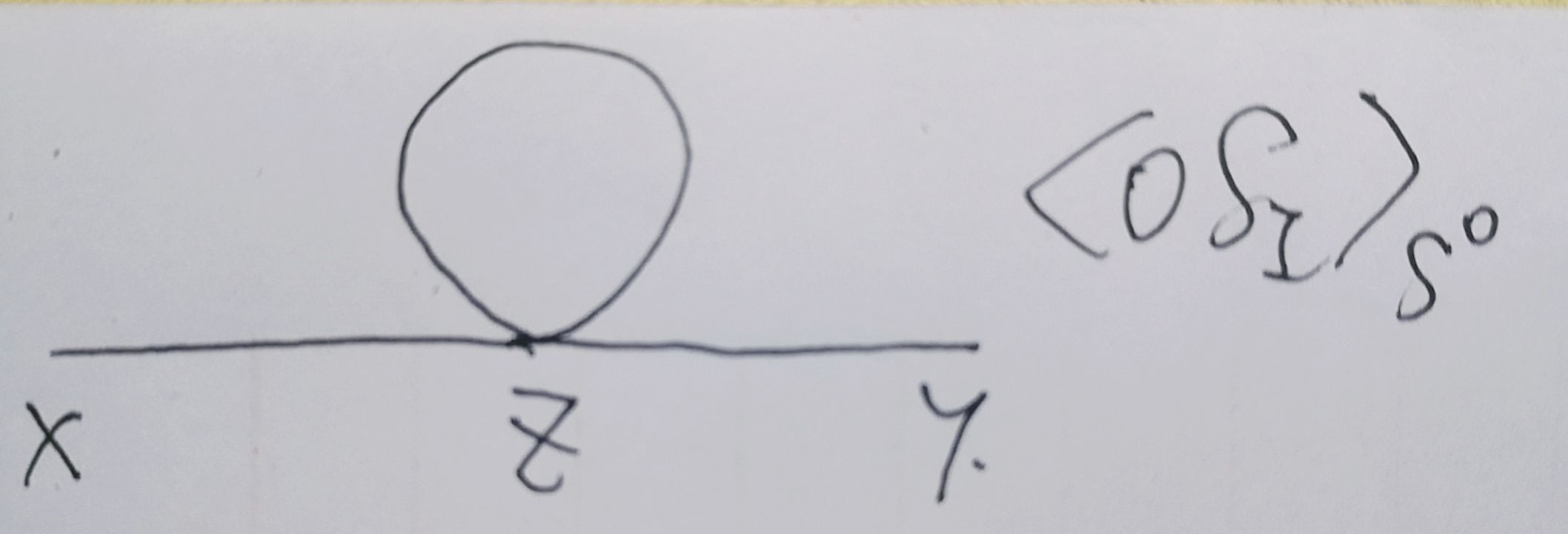 \(=\sum_k\frac{1}{k^2+m^2}=\frac{1}{(2\pi)^d}\int d^dk\frac{1}{k^2+m^2}=\frac{\Omega_d}{(2\pi)^d}\int_{b\wedge}^{\wedge}\frac{k^{d-1}dk}{k^2+m^2}\)
\(=\sum_k\frac{1}{k^2+m^2}=\frac{1}{(2\pi)^d}\int d^dk\frac{1}{k^2+m^2}=\frac{\Omega_d}{(2\pi)^d}\int_{b\wedge}^{\wedge}\frac{k^{d-1}dk}{k^2+m^2}\)
 \(\propto\sum_q\frac{1}{q^2+m^2}\frac{1}{(q+k)^2+m^2}\simeq S_d\wedge^{d-4}(1-b)\)
\(\propto\sum_q\frac{1}{q^2+m^2}\frac{1}{(q+k)^2+m^2}\simeq S_d\wedge^{d-4}(1-b)\)