5.16 周一
- 参考：
- 额外补充引理：参考中国科学技术大学微积分学导论上册
对微分方程\(y'(x)+p(x)y(x)=f(x)\)解为\(y(x)=e^{-\int ^x p(x')dx'}[\int ^x f(x')e^{\int ^{x'} p(x'')dx'}dx'+C]\) - 本学期最后一次作业，作业8：推导本文献中所有公式，也等于说重复出该文献所有结果
- 本节主题：Brown Motion\(\rightarrow\)单粒子\(\rightarrow\)场\(\rightarrow\)非线性(KPZ方程)
Wilson Renormalization Group 1971-1972\(\rightarrow\) Shang-Keng Ma 1973-1974推广到随机非线性方程\(\frac{\partial S_a}{\partial t}=-\frac{\beta}{\mu}\frac{\partial H}{\partial S^a}+\eta_a\)，其中\(\eta_a\)为随机力，\(\frac{\partial H}{\partial S^a}\)为梯度力
后面发展出了Dynamical Renormalization Group方法，参考Flocks,herds,and schools
表面生长问题、细菌生长问题，细菌生长高度为\(h(x,t)\)，定义方差\(w^2(L,t)=\frac{1}{L}\int_0^Ldx(h(x,t)-\bar{h})^2\),\(w\sim L^xf(t/L^z)\)，实验结果为\(x=\frac{1}{2},z=\frac{3}{2}\)
Edwards-Wilklson方程\(\frac{\partial h}{\partial t}=D\triangledown^2 h+\eta\)，KPZ修改为\(\frac{\partial h}{\partial t}=\nu\triangledown^2h+\eta+(\triangledown h)^2\)
微扰求解办法：很类似朗道力学中求解非线性方程的办法，视\(\frac{\lambda}{2}(\triangledown h)^2\)为微扰
令微扰求解值为\(h=h_0+\lambda h_1+\lambda^2h_2+\lambda^3h_3+\cdot\cdot\cdot\),\(\frac{\partial h_0}{\partial t}=\nu\triangledown^2h_0+\eta\)，慢慢微扰求解即可，这也是 - 继续上节课所叙述的过阻尼
\(m\ddot{x}=-\frac{1}{\mu}\dot{x}+f+\xi\)，当\(\frac{1}{\mu}\)很大时，为过阻尼情形，有\(\frac{1}{\mu}\dot{}=f+\xi\rightarrow\dot{x}=\mu f+\eta,\eta=\mu\xi\)，其中\(\mu f\)为阻力，\(\eta\)为随机力
从图像上看来理解\(t<< t_0\)时\(\eta\)不重要，因为粒子初始运动快；当\(t>> t_0\)时，\(\eta\)项更重要，因为粒子运动速度变慢了 - 下列讨论外势能为抛物势，\(f=-kx\)情形，方程为\(\dot{x}=-\mu kx+\eta\)
该微分方程解为\(X(t)=X(0)[e^{-\mu kt}+\int_0^te^{-\mu k(t-t')}\eta(t')dt']\)，故可将X(t)分解为确定部分和不确定部分，\(X(t)=X_1+X_2,\bar{X(t)^2}=\bar{X_1^2}+\bar{X_2^2}+2\bar{X_1X_2}\)
\(\langle x^2\rangle-\langle x\rangle^2=X^2(0)\int_0^t\int_0^te^{-\mu k(t-t_1)}\langle\eta(t_1)\eta(t_2)\rangle e^{-\mu k(t-t_2)}dt_1dt_2=X^2(0)\int_0^t\int_0^t e^{-\mu k(2t-t_1-t_2)}2D\delta(t_1-t_2)dt_1dt_2\)
当\(t\rightarrow+\infty\)时,\(\langle x^2\rangle-\langle x\rangle^2=X^2(0)\frac{D}{\mu k}\)
更正：平衡态时\(P\sim e^{-\beta u}=e^{-\frac{\beta}{2}kx^2}\),\(\langle x^2\rangle=\frac{\int x^2e^{-\frac{\beta k}{2}x^2}dx}{\int e^{-\frac{\beta}{2}kx^2}dx}=\frac{1}{\beta k}\)
我们一般认为\(t\rightarrow+\infty\)时系统趋近于平衡态，故有\(\frac{2DX^2(0)}{2\mu k}=\frac{1}{\beta k}\rightarrow D=\frac{k_BT\mu}{X^2(0)}\) - 下面我们讨论标度行为不变性
\(\frac{d}{dt}X(t)=-\mu X(t)+\eta(t)\)，定义符号：没有标度变换时候为\(X(t),\mu,D,\eta(t)\)，有标度变换时候\(t'=bt\)为\(x'(t'),\mu',D',\eta'(t')\)
\(\frac{dX(t)}{dt}=-\mu X(t)+\eta(t),\frac{dX'(t')}{dt'}=-\mu'X'(t')+\eta'(t')\)，令\(\eta'(bt)=b^{\sigma}\eta(t)\)，则\(\langle\eta'(t'_1)\eta'(t'_2)\rangle=2D'\delta(t'_1-t'_2)=2D'\delta[b(t_1-t_2)]=2D'b^{-1}\delta(t_1-t_2)\)，故\(D'=Db^{2\sigma+1}\)
可类比量子场论下标度变换后波函数形式\(\phi'(k')=\phi'(bk)=b^z\phi(k)\)，定义\(X'(bt)=b^zX(t)\)，则标度变换后方程为\(\frac{b^z}{b}\frac{dX(t)}{dt}=-\mu'b^zX(t)+b^{\sigma}\eta(t)\rightarrow \frac{dx}{dt}=-\mu'bx+b^{\sigma+1-z}\eta\)，有\(\mu'=\mu/b\)
魏贤昊认为的标度变换：类似于变换单位制，若如此，则对于\(\langle x^2\rangle=2Dt\)，则存在两个独立的单位，米和秒，则存在两个自由参量，b和z。我们可以取\(z=\frac{1}{2}\)求得\(\sigma=-\frac{1}{2}\)
讨论\(\frac{\partial h(x,t)}{\partial t}=\nu\triangledown^2h(\vec{x},t)+\eta(\vec{x},t),\langle\eta(\vec{x},t)\eta(\vec{x'},t')\rangle=2D\delta(\vec{x}-\vec{x'})\delta(t-t')\)的标度变换
\(\frac{\partial h(x,t)}{\partial t}=\nu\frac{\partial^2h}{\partial x^2}+\eta(\vec{x},t),\frac{\partial h'(x',t')}{\partial t'}=\nu'\frac{\partial^2h'(x',t')}{\partial x^2}+\eta'(x',t')\)
令\(x'=bx,t'=b^zt,h'(x',t')=b^xh(x,t),\eta'(x',t')=b^{\sigma}\eta(x,t)\)，则标度变换后方程为\(b^{x-z}\frac{dh(x,t)}{dt}=\nu'b^{x-2}\partial_x^2h+b^{\sigma}\eta\rightarrow\frac{dh}{dt}=\nu'b^{z-2}\partial_x^2h+b^{\sigma+2-x}\eta\)
讨论此模型下的标度变换，有\(z=2,x=2+\sigma\)，其中有两个自由度，b和\(\sigma\)
定义\(\langle\eta'(x'_1,t'_1)\eta'(x'_2,t'_2)\rangle=2D'\delta(x'_1-x'_2)\delta(t'_1-t'_2)=2D'\delta[b(x_1-x_2)]\delta[b^z(t_1-t_2)]=2D'b^{-(d-1)-z}\delta(x_1-x_2)\delta(t_1-t_2)\)
有\(b^{2\sigma}\langle\eta(x_1,t_1)\eta(x_2,t_2)\langle=2Db^{2\sigma}\delta(t_1-t_2)\delta(x_1-x_2)\)，由于b和\(\sigma\)是两个自由度，我们可以让\(D=D'\)取此规范下可求出\(\sigma=\frac{-(d-1)-z}{2},x=2+\sigma\)
加入非线性系数\(\frac{\lambda}{2}(\triangledown h)^2\)，其中\(\frac{\lambda'}{2}(\triangledown'h')^2=\frac{\lambda'}{2}b^{2x-2}(\triangledown h)^2\),则有\(\lambda'=\lambda\cdot b^{d+1-z}\) - 考察随机势下动量空间的运动，\(\frac{\partial h(\vec{x},t)}{\partial t}=\nu\triangledown^2h+\eta,\frac{\partial h(\vec{k},t)}{\partial t}=-\nu k^2h(\vec{k},t)+\eta(\vec{k},t)\)，其中\(\langle\eta(k,t)\eta(k,t')\rangle=2D\delta(t-t')\)
解的形式为\(h(\vec{k},t)=h(\vec{k},0)[e^{-\nu k^2t}+\int_0^te^{-\nu k^2(t-t')}\eta(k,t')dt']\)，有\(\langle h^2(x,t)\rangle-\langle h(x,t)\rangle^2=\sum_k\frac{h^2(k,0)}{\nu k^2}\)，Feynman图如下所示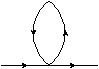
\(d=1\)情况下为红外发散，\(d=2\)情况下同时存在红外发散和紫外发散，\(d=3\)情况下存在紫外发散
\(\sum_x\langle h^2(x,t)\rangle=\sum_k\langle h(k,t)h(-k,t)\rangle=\sum_k\int_0^t 2D\delta(t'-t'')e^{-\nu k^2(t-t')}e^{-\nu k^2(t-t'')}dt'dt''=2D\sum_k\int_0^te^{-2\nu k^2(t-t')}dt'=\sum_k\frac{D}{\nu k^2}(1-e^{-2\nu k^2t})\)
上式\(=2D\Omega_d(\frac{1}{2\pi})^d\int_0^{\wedge}\frac{dk k^{d-1}}{\nu k^2}(1-e^{-2\nu k^2t})\)，令\(\nu k^2t=y^2,y=\sqrt{\nu t}k=2D(\frac{1}{2\pi})^d\frac{1}{\nu}(\sqrt{\nu t})^{d-2}\int_0^{+\infty}\frac{y^{d-1}}{y^2}(1-e^{-2y})dy\sim t^{(d-2)/2}\int_0^{\wedge}\frac{y^{d-1}}{y^2}(1-e^{-2y})dy\)
学生笔记
学生笔记2
学生笔记3
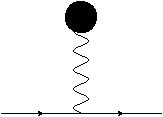\(\rangle=0\),\(\langle\)
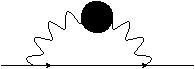\(\rangle\neq0\)
