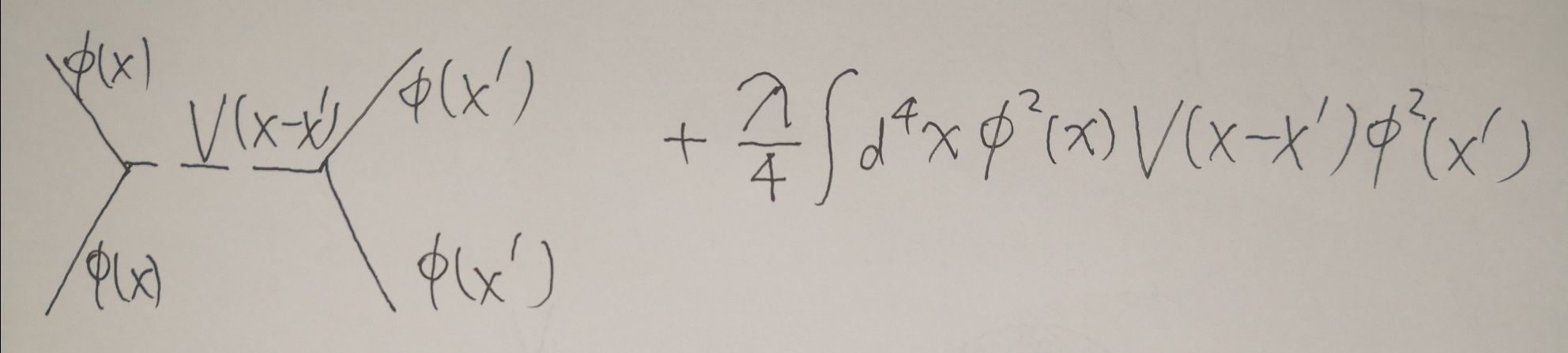• 返回上级菜单

  • 3.21 周一

    1. 回顾之前内容
      2d\(\delta(x)\)势：\(E=-\frac{\hbar^2\bigwedge^2}{2m}e^{-\frac{\hbar^2}{m\lambda(\bigwedge)}}\)，电荷重整化\(e^*\rightarrow\frac{(p-e^*A)^2}{2m}\)
      能标为\(\bigwedge\)，实验测量能标只能为\(\mu<<\lambda\)，实验测得结果为\(\lambda=\lambda(\mu)\)，而\(\lambda(\bigwedge)\)不可测
      \(\phi^4\)理论修正：\(m^2=m_0^2+A\lambda\sum_k\frac{1}{k^2+m^2},\lambda=\lambda_0+\lambda_0^2B\sum_k(\frac{1}{k^2+m^2})^2\)，详细叙述见上节课讲义
      重整化核心：
      1. 用发散抵消发散
      2. 要区分可观测质量\(m_R\)和自由质量\(m_0\)
      3. 重整化是系统的一套方法，可处理多个问题，见Peskin书chap12-13
      4. \(\phi=\sqrt{Z}\phi_R,L=L_R+\delta L\)，其中设置参数使\(\delta L\)为抵消项，使得\(\infty-\infty=\)有限

      重整化广泛应用于量子场论和凝聚态理论中，常常用于处理相变(最早是Ising Model来重整化，后续拓展到相变，常常得到临界点附近发散值\(c_v,\kappa\sim\frac{1}{|T-T_c|^{\nu}}\))
    2. Ising Model简介
      Ising生平只发了3篇论文，其中以Ising model最出名，可参考ising生平。他师从Lenz，Lenz给他提出既然地球磁极有南北极，为什么不能用此来研究固体磁性呢，于是Ising将南北极磁性照搬到固体中，解释固体磁化。这是第一个严格求解的多体Model，Ising的解释很成功又很漂亮
      Heisenberg看了后，觉得Ising只用了\(\sigma_z\)算子，为什么不能拓展到所有方向呢，于是有了Heisenberg模型\(H=-J\sum_{\langle ij\rangle}\vec{S}_i\cdot\vec{S}_j\)
      Onsager严格求解2D Ising Model观测到有相变，获Nobel Prize，现在凝聚态领域有Onsager奖专门纪念Onsager，onsager原始论文(注：Onsager严格求解步骤太多公式太复杂，本课程不要求掌握)
      杨振宁思考了好久做了好久，几年内一直想2D Model有无严格解，最后看到Onsager论文被启发，做出了某个物理量临界指数\(\sim|T-T_c|^{-1/8}\)，是杨振宁13个代表性工作之一，超越了Landau相变理论，杨振宁原始论文(注：本课程不要求掌握)
      Kadanoff、Widom发展了重整化方法来处理，Kadanoff Method就是今天要讲的方法，Wilson在动量空间中发明了重整化方法发了PRB拿了诺奖又tenured
      后来发展了密度矩阵重整化群DMRG，在多体强关联计算中很常用
    3. Ising Model精确解和重整化Kadanoff方法参考：kardar6.1-6.3节
      Ising Model重整化Kadanoff方法，参考：现代统计力学导论5.6节，核心思想和美国大选差不多，我们用一个大州整体站在拜登或特朗普一边，来Trace掉州内个体的选择。在物理中，我们是对一张非常高精度的图片不断减小像素不断模糊化，最后看到一张马赛克图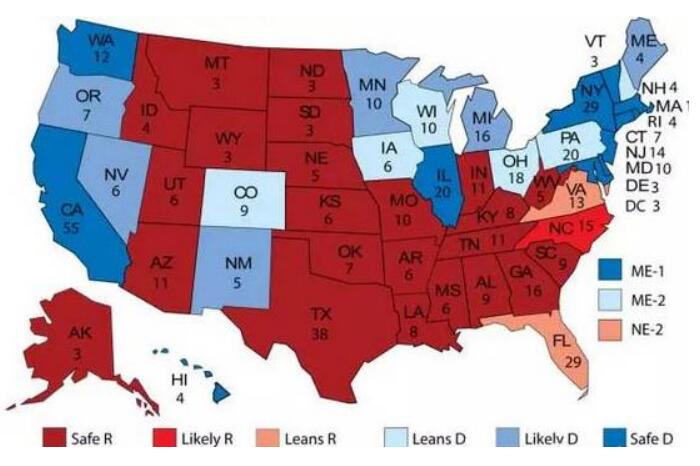


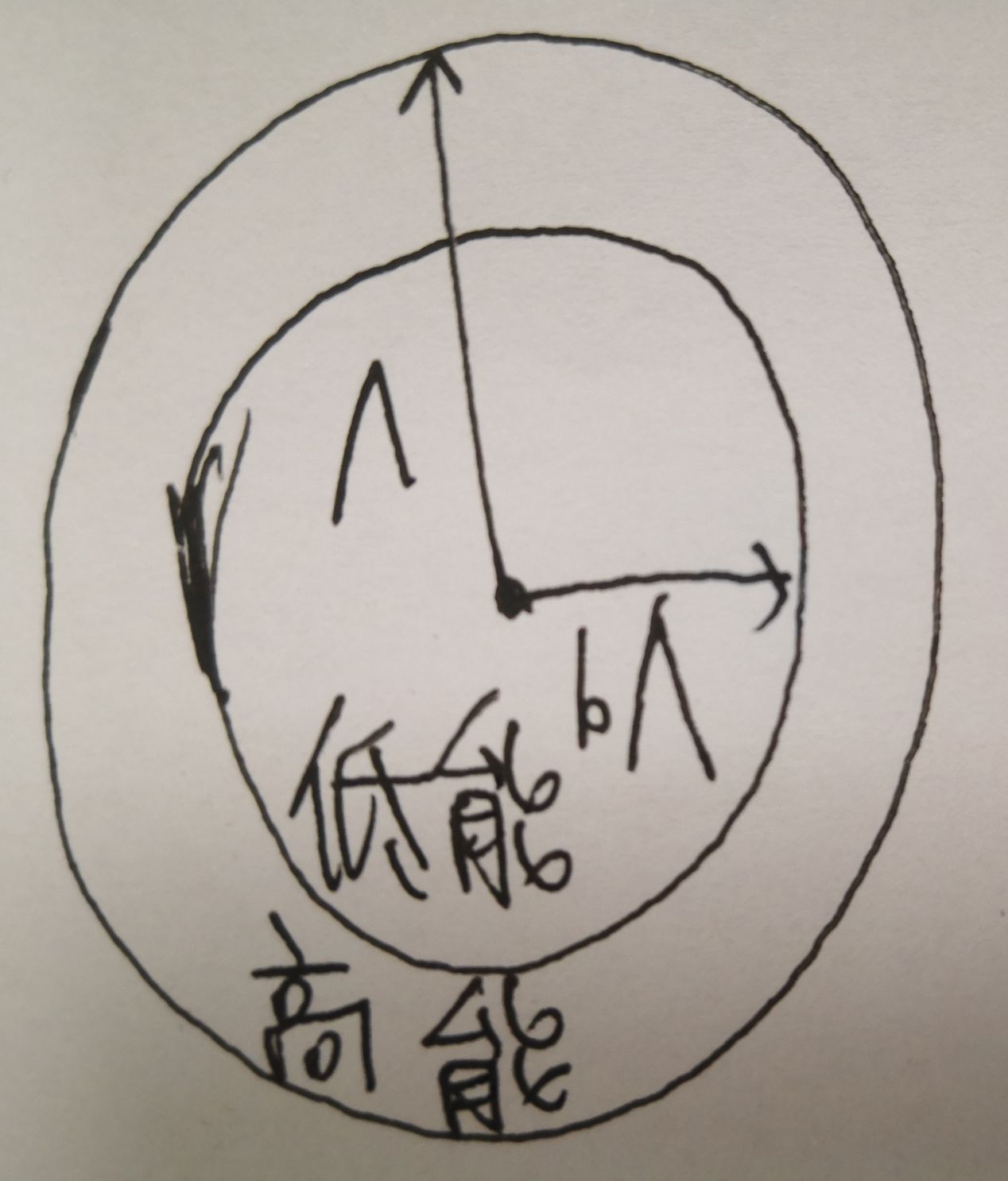
      一般低尺度，比如原子核及附近尺度，对应高能区域；而高尺度，比如数百个分子尺度，对应低能区域。在凝聚态中，我们只关心流体的性质而不关心流体中原子的性质，因此我们不断要对高能部分进行重整化，增加尺度，最终过渡到低能部分
      \(Z=Tr(e^{-\beta H})=\sum_{\{S_i=\pm1\}}e^{K\sum_iS_iS_{i+1}}=\sum_{\text{奇}}\sum_{\text{偶}}e^{K\sum_iS_iS_{i+1}}=\sum_{\text{奇}}e^{\sum_iK'S_{2i-1}S_{2i+1}}\)
      \(\sum_{S_2=\pm1}e^{KS_1S_2+KS_2S_3}=e^{K(S_1+S_3)}+e^{-K(S_1+S_3)}=Ae^{K'S_1S_3}\rightarrow K'=\frac{1}{2}lncosh(2K),A=2\sqrt{cosh(2K)}\)
      重整化过程如下图所示：对一个1D无限长格点，\(Z=Tr[e^{-\beta H}]\)，每次Tr掉偶数格点，于是又重整化flow:\(K_1\rightarrow K_2\rightarrow K_3\rightarrow\cdot\cdot\cdot K_n\)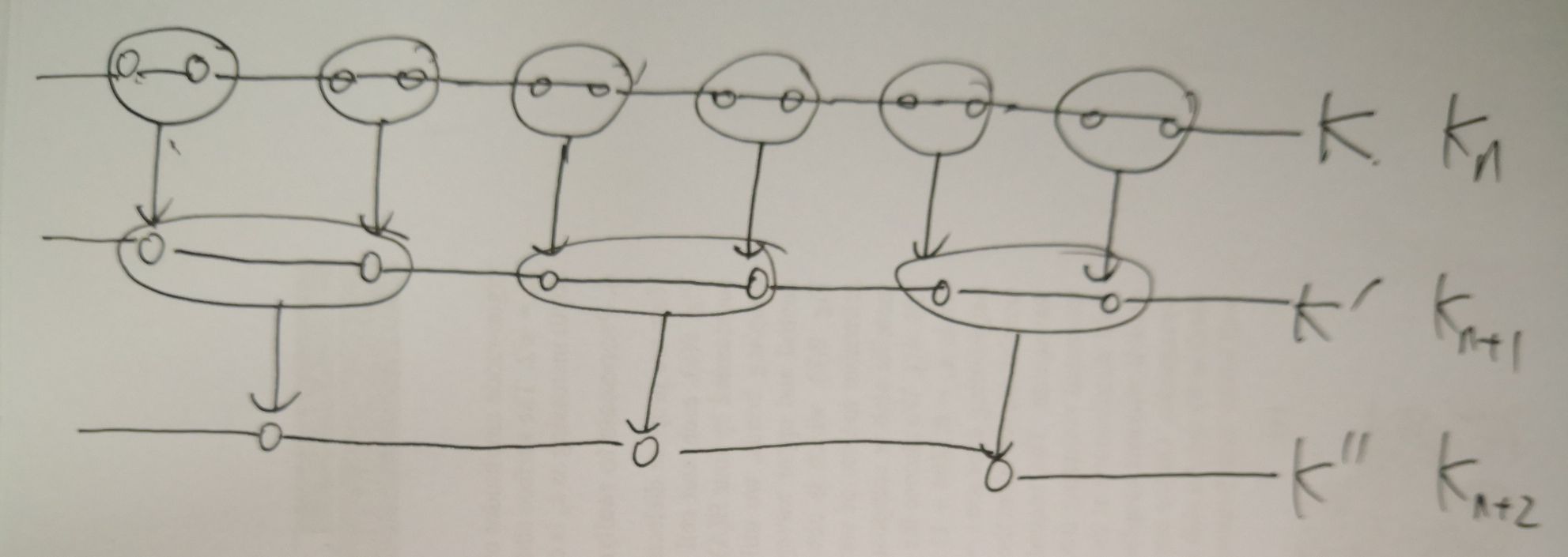


      \(K_{n+1}=\frac{1}{2}lncosh(2K_n)\)，最后结果如下所示


      \(K=\beta J\)，故只有两个稳定点\(T\rightarrow0和T\rightarrow+\infty\)，对于有限温的物理，重整化慢慢流向无限温。故在有限温下，1D Ising model链中磁自旋完全无序排布，1D Ising model无相变
      2D Ising Model，三角晶格Ising Model用此方法只能得到近似解(本课程不要求掌握)，2D和三角晶格都可参考：kardar6.4-6.5节，2D参考资料：现代统计力学导论5.7节，三角晶格参考资料高等统计力学导论第六章，苏汝铿书第七章
      Lyapnov index:最早起源于混沌和无序，当初始体系由微小偏离时，末态指数偏离\(dx_n=e^{n\lambda}dx_0\),\(\lambda\)为Lyapnov指数
      \(K_{n+1}=R(K_n)\rightarrow \delta K_{n+1}=R'(K_n)\delta K_n\rightarrow\delta K_n\propto e^{R'(K_n)-1}\)
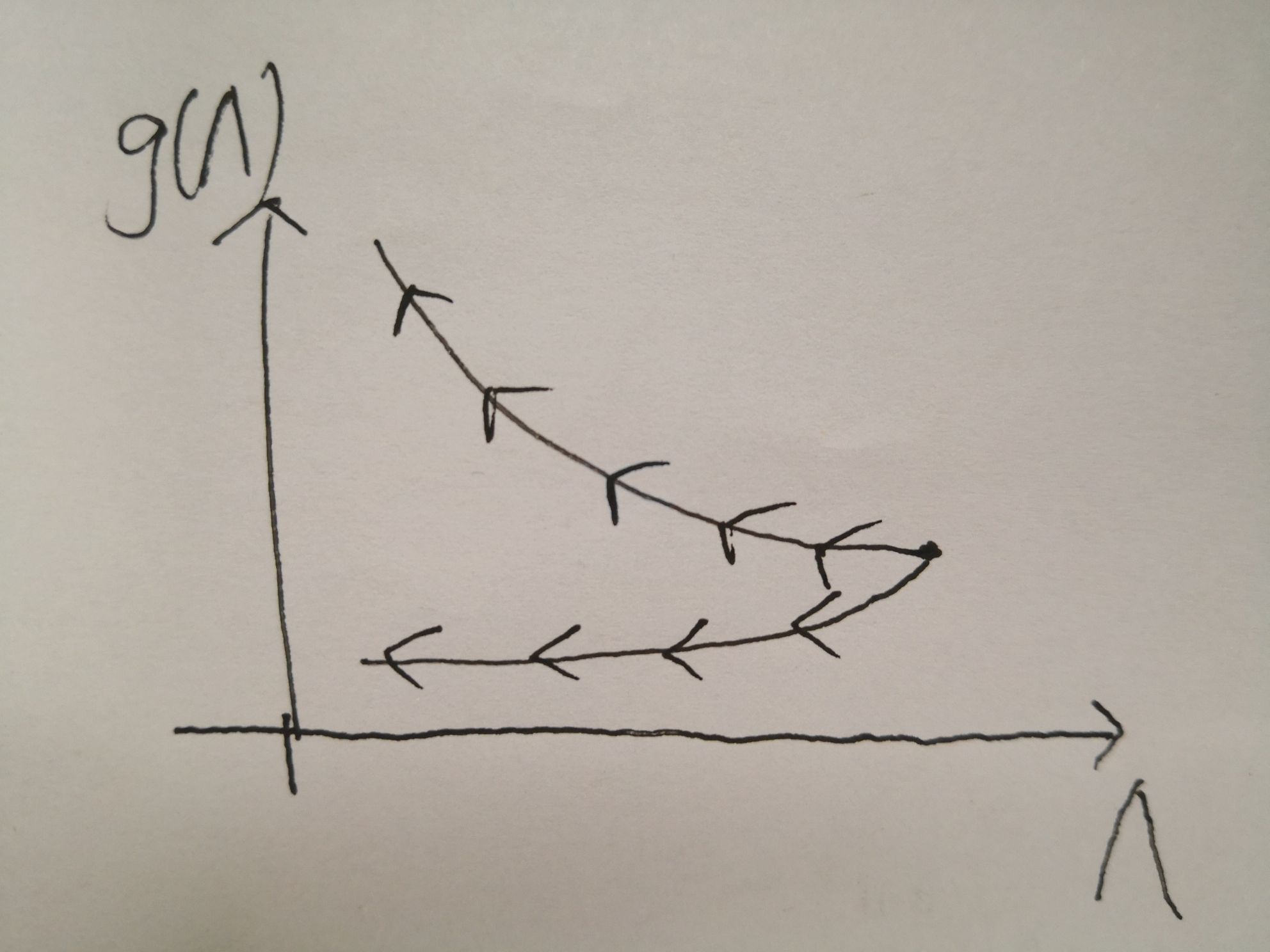
      重整化流如下图所示：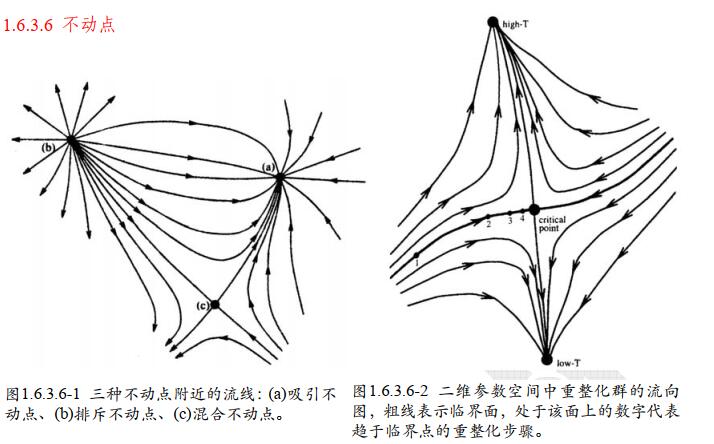

    4. \(\phi^4\)理论重整化：参考Peskin书chap12-13
      我们先来讨论重整化后相互作用系数的变化，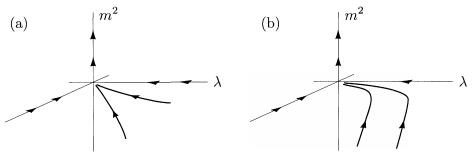


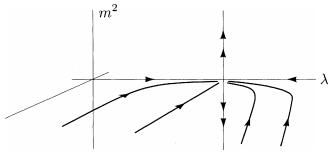
      讨论标度率变化：\(L=\frac{1}{2}(\partial\phi)^2-\frac{m^2}{2}\phi^2-\frac{\lambda}{4!}\phi^4\)，之后叙述m表示米,\(S=\int d^DxL,L=[m]^{-D},\phi=[m]^{-D/2+1},\lambda=[m]^{D-4}\)
      重整化：慢慢Tr掉高能部分，保留低能部分，慢慢让尺度变大\(L\rightarrow sL(s>1)\),\(\phi^4\)理论相互作用系数\(\lambda\)放大\(s^{D-4}\)倍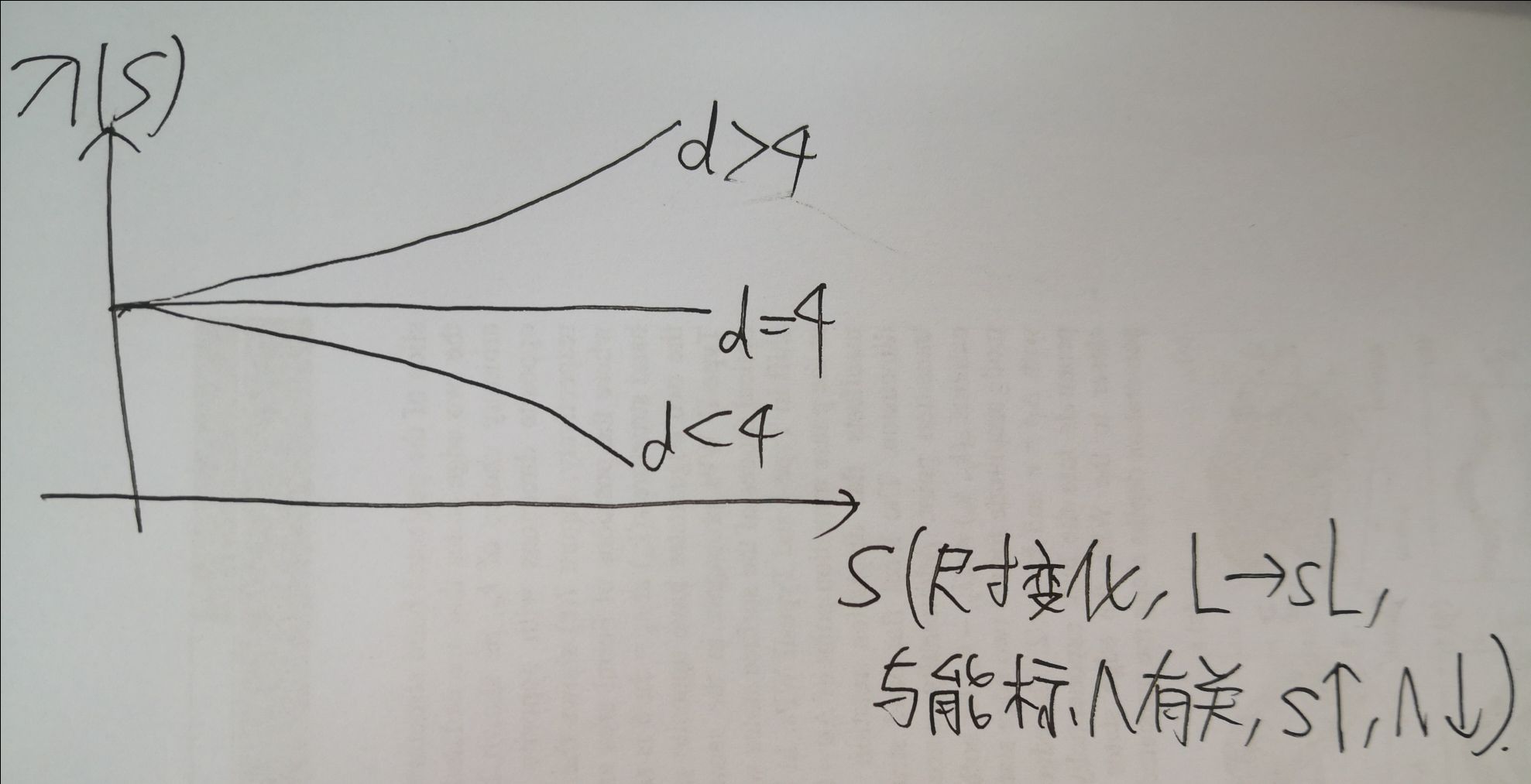

    5. Naiver-Strokes Equation，参考我写的Note
    6. 作业2：推导以下文献(二选一) :
      PhysRevLett.31.1411
      PhysRevB.15.3460.pdf
      学生笔记
      学生笔记2
      学生笔记3

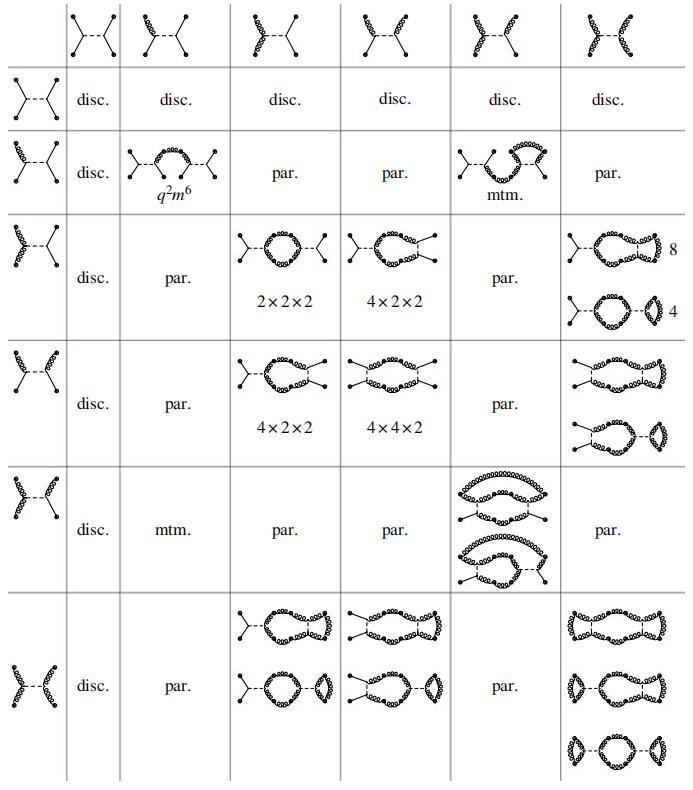
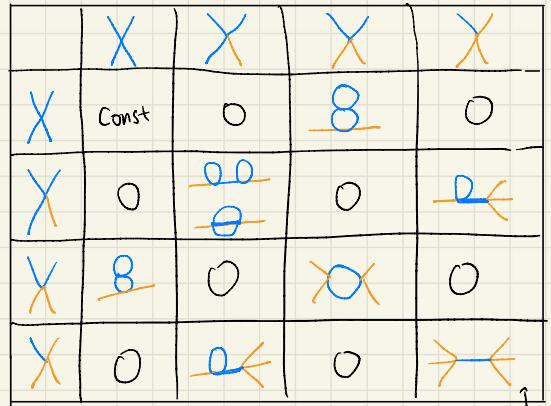
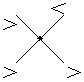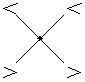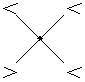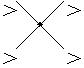  • 3.24 周四

    1. 本节可参考：Shankar13、14节
    2. 回顾上节课：Ising Model进行重整化，不断Tr掉偶数格点，在这个过程中要损失很多细节，就像打了马赛克一样，同时也要损失掉高能部分
    3. 今天要讲的是Wilson工作，将这个思想应用到动量空间，如下图所示：


      凝聚态中我们一般关注低能标情形，能标越低就越接近平均场理论。当能标越低相互作用越小时，越接近单体物理越好求近似解，但是当能标越低相互作用越大时，平均场理论可能失效，不好求多体解
      \(L=\frac{1}{2}(\partial\phi)^2-\frac{m^2}{2}\phi^2-\frac{\lambda}{4!}\phi^4\)，令\(t=-i\tau\)，其中\(\tau\)为虚时，\(\int dtd\vec{x}=-i\int d\tau d\vec{x}\)
      路径积分公式变为：\(Z=\int D\phi e^{-S},S=\int Hdx,dx=d\tau d\vec{x},S=\int dx\{\frac{1}{2}(\partial\phi)^2+\frac{m^2}{2}\phi^2+\frac{\lambda}{4!}\phi^4\}\)
      \(S=\sum_{|k|\leq\wedge}\frac{k^2+m^2}{2}\phi_k^*\phi_k+\frac{\lambda}{4!}\sum_{|k|,|k'|,|q|,|k+k'+q|\leq\wedge}\phi_k\phi_{k'}\phi_q\phi_{-k-k'-q}\)
    4. Wilson重整化思想：缩小能标\(\wedge\rightarrow b\wedge\)，不断将高能部分\(b\wedge\leq |k|\leq\wedge\)Tr掉，来得到只有低能部分\(|k|\leq b\wedge\)的作用量


      \(S=S^{\langle}+S^{\rangle}+\delta S\)

      \(S^{\langle}=\sum_{|k|\leq b\wedge}\frac{k^2+m^2}{2}\phi_{\langle}^*\phi_{\langle}+\frac{\lambda}{4!}\sum\)
      \(S^{\rangle}=\sum_{b\wedge\leq|k|\leq\wedge}\frac{k^2+m^2}{2}\phi_{\rangle}^*\phi_{\rangle}\)
      \(\delta S=\frac{\lambda}{4!}\)(+++)

      \(Z=\int D\phi_{\langle}e^{-S_{\langle}}\int D\phi_{\rangle}e^{-(S_{\rangle}+\delta S)}\)
      \(\int D\phi_{\rangle}e^{-(S_{\rangle}+\delta S)}=(\int D\phi_{\rangle}e^{-S_{\rangle}})\frac{\int D\phi_{\rangle}e^{-(S_{\rangle}+\delta S)}}{\int D\phi_{\rangle}e^{-S_{\rangle}}}=const*\langle e^{-\delta S}\rangle_{S_{\rangle}}\)
      \(\langle e^x\rangle=e^{\langle x\rangle_c-\frac{1}{2}\langle x^2\rangle_c}\)
      故\(Z=\int D\phi_{\langle}e^{-S_{\langle}}*const*\langle e^{-\delta S}\rangle_{S_{\rangle}}=\int D\phi_{\langle}e^{-\int S_{\langle}+\triangle S_{eff}}\)
      \(\triangle S_{eff}=\langle \delta S\rangle_{S_{\rangle}}^c+\frac{1}{2}\langle\delta S^2\rangle_{S_{\rangle}}^c\)，下列我们讨论一阶项情形，其中部分图不能配对，如下所示：
      +(不能配对，不是连通图)，(能配对，是连通图)
      计算一阶修正：\(\langle\delta S\rangle_{S_{\rangle}}=\frac{\int D\phi_{\rangle}^*D\phi_{\rangle}e^{-S_{\rangle}}(\triangle S)}{\int D\phi_{\rangle}^*D\phi_{\rangle}e^{-S_{\rangle}}}\)
      \(\delta S=\frac{\lambda}{4!}\sum_{\rangle}\phi_k\phi_{k'}\phi_q\phi_{-k-k'-q}\)
      \(\langle\delta S\rangle_{S_{\rangle}}=const+\frac{\lambda}{4!}C_4^2\phi_{k_{\langle}}^*\phi_{k_{\langle}}\sum_{b\wedge\leq|q|\leq\wedge}\frac{1}{q^2+m^2}\)
      \(\sum_{b\wedge\leq|q|\leq\wedge}\frac{1}{q^2+m^2}=\frac{\Omega_d}{(2\pi)^d}\int_{b\wedge}^{\wedge}\frac{q^{d-1}}{q^2+m^2}dq\simeq\frac{\Omega_d}{(2\pi)^d}\frac{\wedge^{d-1}(\wedge-b\wedge)}{\wedge^2+m^2}\simeq\frac{\Omega_d}{(2\pi)^d}\wedge^{d-2}(1-b)\)
      故\(\langle\delta S\rangle_{S_{\rangle}}=const+\delta m^2\phi_{k_{\langle}}^*\phi_{k_{\langle}}\)
      一阶修正后表达式：\(S^{\langle}=\sum_{|k|\leq b\wedge}\frac{k^2+m^2+\delta m^2}{2}\phi_k^*\phi_k+\frac{\lambda}{4!}\sum_{|k|\leq b\wedge}\phi_k\phi_{k'}\phi_q\phi_{-k-k'-q},\delta m^2=\frac{\lambda}{2}\Omega_d\wedge^{d-2}(1-b)\)
      计算二阶修正：，参考Shankar13、14节


      注：上图中虚线表示相互作用，对于\(\phi^4\)理论没有这个虚线。这个带虚线费曼图表示如下所示相互作用


      上图：黄线为小于，蓝线为大于
      表格为0的部分：配对不充分，无法形成有效连通图
      表格第二行第二列第一张图：配对后动量不守恒，表格第二行第二列第二张图：目前没办法计算，算不出来，且大量文献计算表明该图不重要，最后只能得到\(m^2\)的高阶修正而不是\(\lambda\)的修正
      表格第二行第四列：配对后动量不守恒
      表格第四行第四列：只有可能在靠近\(b\wedge\rightarrow\wedge\)区域内该图才有贡献，而这又是没办法处理的，因为只积掉高能区域，最后只能得到\(\phi^6\)的高阶修正而不是\(\lambda\)的修正
      表格第三行第一列：\(\sum_{b\wedge\leq|q|\leq\wedge}\frac{1}{q^2+m^2}\propto 1-b\)，最后结论是图\(\propto(1-b)^2\)，为二阶小量，舍去
      故对\(\lambda\)的一阶修正只有表格第三行第三列有贡献
      学生笔记：\(-\frac{1}{2}\langle\triangle S^2\rangle_{S_{\rangle}}^c=-\frac{1}{2}\frac{\lambda^2}{4!}\sum_{k_1,k_2,k_3,k_1+k_2+k_3\leq b\wedge}\phi_{k_1}\phi_{k_2}\phi_{k_3}\phi_{-k_1-k_2-k_3}\sum_{b\wedge\leq|q|\leq\wedge}\frac{1}{q^2+m^2}\frac{1}{(q-k_1-k_2)^2+m^2}*6*6*2\)
      无数次重整化缩小能标，我们最终目的是只关心最低能区域，因此只保留\(k_1,k_2,k_3\langle\langle\wedge\)的部分，有
      \(-\frac{1}{2}\langle\triangle S^2\rangle_{S_{\rangle}}^c=-\frac{\delta\lambda}{4!}\sum_{k_1k_2k_3}\phi_{k_1}\phi_{k_2}\phi_{k_3}\phi_{-k_1-k_2-k_3},\delta\lambda=\frac{3}{2}\Omega_d\wedge^{d-4}(1-b)\)
      学生笔记
      学生笔记2