- 考试:50%,开卷(5选4)
- 课题报告:20% (格式8%,内容12%)
- 平时作业:30% (作业每两周交一次)
作业1-16答案参考 作业17-29答案参考
第七次作业35-40,6月24日之前交。以往没有交作业的在考试之前补交上。纸质电子版都可以,内容包括题目代码结果,有证明之类的写必要推导过程。 代码粘贴到word或pdf与结果放一起,不要只交.m/.py/.nb等源代码。电子版发到邮箱xhz1995@mail.ustc.edu.cn,主题“计算物理-姓名-学号”,以免漏掉。 若交邮箱,收到后我会回复大家,没有收到回复的联系我。大家尽量按时交,晚交的酌情扣分。 - 优秀作业参考
作业1-6 作业7-12 作业13-18 作业19-24 作业25-29 作业30-34 作业35-40
- 统计表 大家把不能参加考试的时间或者建议考试的时间填一下!
- 考试时间6月25日上午8-11点,地点5106。
- 主要内容:插值方法
(1) 过\((x_1,y_1),(x_2,y_2)\)两点插值: \[y=\frac{x-x_1}{x_2-x_1}y_2 + \frac{x-x_2}{x_1-x_2}y_1 \]
(2) 过\((x_1,y_1),(x_2,y_2),...,(x_N,y_N)\) N点插值: \[y=\sum_i^N l_i(x) y_i, \quad l_i(x) = \frac{(x-x_1)(x-x_2)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_N)}{(x_i-x_1)(x_i-x_2)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_N)}\]
(3) \(l_i(x)\)性质:
a. \(l_i(x_j) = \delta_{ij}\)
b. \(l_i(x)\)只和\(x_i\)有关与\(y_i\)无关,是\(x\)的\(N-1\)阶函数
c. \(l(x)=\sum_i^N l_i(x) = 1\)
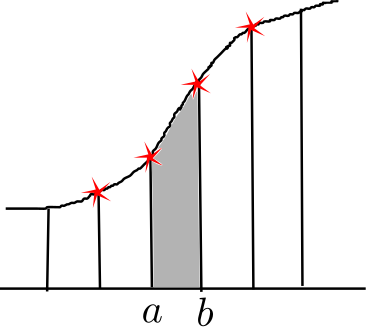
(4) 误差 \[ R_N(x) = \frac{f^N(\xi)}{N!}(x-x_1)\cdots(x-x_N)\] - 作业1:已知曲线过四个点(红色标记),确定中间两点a,b之间灰色区域面积。
- 导数问题
(1) 变为积分,进行插值 \[y^{\prime} = f(x) \quad \rightarrow \quad y = \int_{x_0}^{x}f(x^{\prime})dx^{\prime} + y_0 \] (2) 变为迭代方程 \[y^{\prime} = f(x) \equiv \frac{y(x)-y(x-h)}{h} \quad\rightarrow\quad y(x_n) = y(x_{n-1}) + hf(x_{n-1}) \] \[y^{\prime\prime} = f(x) \equiv \frac{y(x+h)+y(x-h)-2y(x)}{h^2} \quad\rightarrow\quad y(x_{n+1}) + y(x_{n-1}) -2y(x_n) = h^2f(x_{n}) \] (3) \(y^{\prime} = f(x,y)\)显式,隐式法(Picard迭代法) - 解方程问题
\(f(x) = 0\)变为迭代方程
Example: \(ax^2+bx+c=0 \quad\rightarrow\quad x_n = -\frac{a}{b}x_{n-1}^2 - \frac{c}{b}\) -
- 作业2:求解方程\(AX^2+BX+C=0\),其中\(A,B,C,X\)均为矩阵。取\(A,B,C\)为任意的\(3\times3\)矩阵,找到满足方程的解的\(X\)。
作业3:质量分别为\(m\)和\(M\)的两球通过劲度系数为\(k\)的弹簧连接,弹簧自然状态长为\(d_0\),初始时刻系统位置、弹簧长度任意选取,若沿\(x\)轴水平抛出,求解之后系统的运动情况,如下图示意。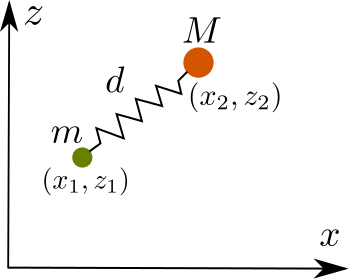
- 主要内容
(1) Forward算法 \[ y_{n+1} = y_n + hf(x_n,y_n) \] (2) Backward算法 \[ y_{n+1} = y_n + hf(x_{n+1},y_{n+1}) \] (3) 预估 \[y_{n+1} = y_n \frac{h}{2} [f(x_n,y_n) + f(x_{n+1},\overline{y}_{n+1})] ,\quad \overline{y}_{n+1} = y_n+h f(x_n,y_n)\] \[\Rightarrow \quad y_{n+1} = y_n + \frac{h}{2} [f(x_n,y_n) + f(x_n+h,y_n+h f(x_n,y_n))] \] (4) Runge-Kutta算法 不用求导数,减少求\(f(x,y)\)的次数。
RK23,2阶,误差\(o(h^3)\);RK45,4阶,误差\(o(h^5)\)。
(5) 矩阵
附:Mathematica代码 - 作业4:RK45算法精度分析
作业5: Baker's map
产生随机序列,画出点图。
作业6: Lorenz Attractor
自选参数,画出系统运动轨迹。
- 量子化
(1) 一次量子化 \([x,p] = i\hbar\)
(2) 二次量子化 Dirac(1927)
\(\{c_n,c_m\} = \{c_n^*,c_m^*\}=0, \{c_n,c_m^*\}=\delta_{nm} \) 等价描述 \(\{\Psi,\Psi\} = \{\Psi^*,\Psi^*\} = 0, \{\Psi(x),\Psi^*(y)\} = \delta(x-y) \)
\(|c_n|^2 = c_n^*c_n\),占据数 \(\Rightarrow\) \(\widehat{n} = c_n^{\dagger}c_n\),粒子数。\( c_n^{\dagger},c_n \)产生湮灭算子 - 附:Mathematica代码-矩阵操作
- 二次量子化refbook
- 随机矩阵
(1).三类高斯系综:GOE,GUE,GSE, (2).联合概率密度函数, (3).半圆率, (4).Wigner假设-能级间距分布, (5).能级间距比分布.
附: Matlab代码,PPT, 参考书, 参考文献 - Bloch定理 \(\Psi_k(x+R) = \Psi_k(x)e^{ikR}, \Psi_k(x) = u_k(x)e^{ikx}, u_k(x+R)=u_k(x)\)
- 扩展态\(\leftrightarrow\)局域态 \(\Psi(x) = \sum_n C_n W_n(x)\), 其中\(W_n(x)\)为Wannier函数,局域态。
- 一维Bose-Hubbard model
\(H = H_0 + V\), \(H_0 = -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \eta \cos(kx)\), 相互作用项\(V=g\delta(x)\)
近似:\( H_0 = -t\sum_{nm}(C_n^\dagger C_{n+1} + h.c.) -\mu C_n^\dagger C_n \), \(V = UC_n^\dagger C_n^\dagger C_nC_n\)
\(H_0\)对角化:\(H_0 = \sum_k (-2t\cos k-\mu) C_k^\dagger C_k\) - 作业7计算GOE,GUE,GSE (1).能级间距比分布\(P(r)\), (2).半圆率, (3).换不同随机数计算,如均匀、正态分布等。矩阵大小可以选择100*100,平均1000次。
- 作业8计算四个粒子\(\langle x_1 x_2x_3x_4|\partial x_1 | x_1 x_2x_3x_4 \rangle \)。
- 作业9相互作用项\(\int dxdy \Psi^\dagger (x)\Psi^\dagger (y) g \delta(x-y) \Psi(y)\Psi(x) = g C^\dagger_{n_1} C^\dagger_{n_2} C_{n_3} C_{n_4}\int W^*_{n_1}W^*_{n_2}W_{n_3}W_{n_4}dx\),若\(C_n\)为费米子,做最低阶近似。
- Mathieu函数 附:Mathematica代码
- Tight-Binding model real space与kspace的对应变换:
(1). \(-t\sum_n c_n^\dagger c_{n+1}+h.c.\) \( \leftrightarrow \) \(-2t\sum_k c_k^\dagger c_{k}\) \(\leftrightarrow\) \(\sum_k (-2t+tk^2) c_k^\dagger c_k\), for \(k \rightarrow 0\)
(2). \(\mu\sum_n c_n^\dagger c_{n} \) \( \leftrightarrow \) \(\mu\sum_k c_k^\dagger c_{k}\)
(3). \(h \sum_n (c_{n \uparrow}^\dagger c_{n\uparrow} - c_{n\downarrow}^\dagger c_{n\downarrow})\) \(\leftrightarrow\) \(h \sum_k (c_{k \uparrow}^\dagger c_{k\uparrow} - c_{k\downarrow}^\dagger c_{k\downarrow})\) (4). \(h \sum_n (c_{n \uparrow}^\dagger c_{n\downarrow} + h.c.)\) \(\leftrightarrow\) \(h \sum_k (c_{k \uparrow}^\dagger c_{k\downarrow} + h.c.)\) (5). \( \sum_{n} ( c_{n\uparrow}^\dagger c_{n+1\downarrow} + h.c. ) \) \(\leftrightarrow\) \( \sum_k (e^{ik}c_{k\uparrow}^{\dagger} c_{k\downarrow} + e^{-ik}c_{k\downarrow}^{\dagger} c_{k\uparrow} )\) (6). \(\lambda \sum_{n} ( c_{n\downarrow}^\dagger c_{n+1\uparrow} + h.c. )\) \(\leftrightarrow\) \( \sum_k (\lambda e^{ik}c_{k\downarrow}^{\dagger} c_{k\uparrow} + \lambda^* e^{-ik}c_{k\uparrow}^{\dagger} c_{k\downarrow} )\) For \(\lambda=1\), (5)+(6) \(\leftrightarrow\) \( \sum_k (2\cos k c_{k\uparrow}^{\dagger} c_{k\downarrow} +h.c.)\) For \(\lambda=i\), (5)+(6) \(\leftrightarrow\) \( \sum_k (2i\sin k c_{k\uparrow}^{\dagger} c_{k\downarrow} +h.c.)\) - 定义Unitcell: \(\overrightarrow{R}\), Unitcell里的原子或轨道: \(\overrightarrow{\tau_\alpha}\) \( H=-\sum_{RR^\prime , \alpha\alpha^\prime} t_{RR^\prime}^{\alpha\alpha^\prime} c_{R\alpha}^{\dagger} c_{R^\prime\alpha^\prime}\) \(\leftrightarrow\) \( \sum_{k\alpha\alpha^\prime} c_{k\alpha}^{\dagger} c_{k\alpha^\prime} t_{k}^{\alpha\alpha^\prime} \) 其中: \( t_{k}^{\alpha\alpha^\prime} =\sum_Q e^{-ikQ}t^{\alpha\alpha^\prime}(Q)\)
- 三带model(三对角矩阵,复杂度\(o(N)\)),对应TB model: \( H =\sum_n^N tc_n^\dagger c_{n+1} +\sum_n^N\mu c_n^\dagger c_n\)
- 作业10 Mathematica里Mathieu函数.(1) 画能带(变化q的大小),(2) 画出Bloch波函数,(3) 计算Wannier函数(Mathematica编程计算)
- 作业11
(1) 图a的k空间\(H_k\)表达式;变化参数问什么时候能带从\(m^*>0\)变为\(m^*<0\) (2) 图b的k空间\(H_k\)表达式;画出能带图.其中\(-t\)近邻跃迁,\(-t^\prime\)次近邻跃迁 (3) 图c的Graphene model的k空间\(H_k\)表达式;画出能带图;什么时候出现Dirac点.其中\(-t\)近邻跃迁,\(-t^\prime\)次近邻跃迁 (4) 将以下两个动量空间的哈密顿量变到实空间,并在正方形格子中画出Tight-Binding model \(H_1 = \frac{k_x^2+k_y^2}{2m} + \lambda (k_x\sigma_x-k_y\sigma_y) -\mu \) \(H_2 = \frac{k_x^2+k_y^2}{2m} + \lambda (k_x\sigma_y-k_y\sigma_x) -\mu \) (5) 写出下面哈密顿量的Tight-Binding model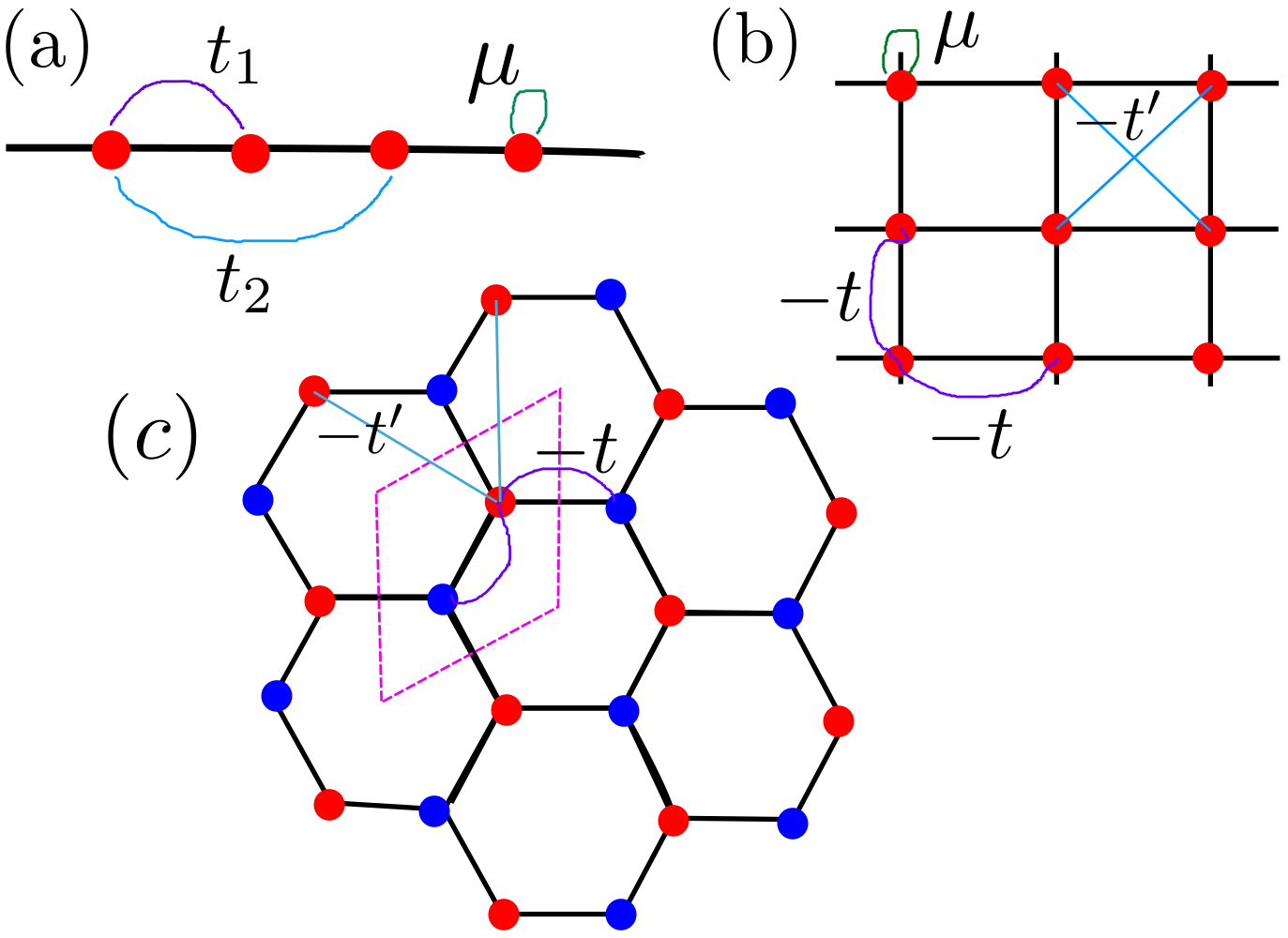
- 三对角矩阵
对应TB model: \( H =\sum_n^L tc_n^\dagger c_{n+1} +\sum_n^L\mu c_n^\dagger c_n\) 两种方法求解: (1) 设\(\psi = \sum_i^L \alpha_i c_i^\dagger |0 \rangle\); 边界条件\(\alpha_0=0,\alpha_{L+1} = 0\) \(\Rightarrow\) \( t(\alpha_{j+1}+\alpha_{j-1}) +\mu \alpha_j = \lambda\alpha_j \) (2) 令\(Q_L = det(H_L)\) \(\Rightarrow\) \(Q_L = (\mu-\lambda)Q_{L-1} - t^2 Q_{L-2} \) 解为: \( \lambda = 2 t \cos(\theta) +\mu \), \(\theta = \frac{2\pi q}{L+1}\) - 差分方法:\( \frac{df^2}{dx^2} = \frac{f_{i+1} +f_{i-1} -2f_i }{(\delta x)^2} \) \(\Rightarrow\) \(\frac{1}{(\delta x)^2}\)
- 二次型哈密顿量
\(H = \sum_{ij} t_{ij} c_i^\dagger c_j + \sum_{ij} \vartriangle_{ij} c_j^\dagger c_j^\dagger + h.c. \) \( \Leftrightarrow \) , \(\psi^\dagger = (c_1^\dagger,\cdots,c_L^\dagger, c_1,\cdots,c_L) \) - 作业12 利用差分方法求解下列哈密顿量
\(H = - \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + \frac{1}{2} m \omega^2 x^2 \)
\(H = - \frac{\hbar^2}{2m} \frac{d^2}{dx^2} + \frac{1}{2} m \omega^2 x^2 +\alpha x^4\)
- 正则
(1) 经典力学: \(X=(q_1,\cdots,q_N,p_1,\cdots,p_N)\) \( \Leftrightarrow \) \( \{ X_i,X_j\} = \Sigma_{ij} \) 若存在\( U \Sigma U^T = \Sigma\) (辛几何) \(\Rightarrow \) \([det(U)]^2=1\),则\(Y=UX\)也是正则的。 (2) 量子力学:\(X^\dagger = (c_1^\dagger,\cdots,c_N^\dagger,c_1,\cdots,c_N)\) \( \Leftrightarrow \) \( \{ X_i,X_j^\dagger\} = \Sigma_{ij} \) , \("-"\)表示Bose子,\("+"\)表示Fermi子。 对于Fermi子,若存在\( U \Sigma U^\dagger = \Sigma\) \( \Leftrightarrow \) \(UU^\dagger=I\),则\(Y=UX\)也是正则的。 对于Bose子,若存在\( U \sigma_z U^\dagger = \sigma_z\),则\(Y=UX\)也是正则的。特别的若\(U\)可以写为块对角形式: , 可以得到\(UU^\dagger=I\) - 经典力学的震动问题:
(1) \(H = A_{ij}p_i p_j + B_{ij} q_i q_j +c_{ij} p_i q_j\) 变为Bose子: 带入上式得: \( \dot{p}_i = -\frac{\partial H}{\partial q_i} = \sum_\beta [-(B_{i\beta} + B_{\beta i})q_\beta + C_{\beta i}p_\beta] \) \( \dot{q}_i = -\frac{\partial H}{\partial p_i} = \sum_\beta [-(A_{i\beta} + A_{\beta i})p_\beta + C_{i \beta}q_\beta] \) \(\Rightarrow\) \(\Rightarrow\) \(\dot{X} = DX\) \(\Rightarrow\) 解为 \(\Rightarrow\) \(X \sim \sum_i X_i e^{i \omega_i t}\) \(\Rightarrow\) \(i\omega X = DX\) (2) 经典力学频率 \(\Leftrightarrow\) 量子力学本征值。 (3) 经典力学的非稳定性 \(\Leftrightarrow\) Bose子的复数解 \(\Leftrightarrow\) 非厄米矩阵 - Hilbert空间与多体作用,多粒子(全同)。例如3个粒子,\(L\)个格点:
(1) Bose子空间维度:\(C_L^3 + 2C_L^2 + C_L\)
(2) Fermi子空间维度:\(C_L^3\) - 作业13 三体系统在平衡位置附近的震动问题:\(H = p_1^2+p_2^2+p_3^2 + \omega^2(x_1^2+x_2^2+x_3^2) + \alpha(x_1x_2+x_1x_3+x_2x_3)\) (1). 求系统的震动过程以及频率; (2). 转化为Bose子模型再求解; (3). 证明(1)与(2)等价(相同的一套代数)。
- 作业14 多体系统求解:
(1). 3个格点,2个粒子的Bose-Hubbard model: \(H = -t\sum_{ij} (b_i^\dagger b_j +h.c.) + \frac{U}{2} \sum_i n_i (n_i-1) \),计算能谱;
(2). 4个格点,2个粒子的Fermi-Hubbard model: \(H = -t\sum_{ij} (c_i^\dagger c_j +h.c.) + U \sum_{ij} n_i n_j \),计算能谱。
- Floquent定理:\(\frac{\partial f}{\partial t} = A(t) f, \quad A(t) = A(t+T) \)
解:\(f=U(t)f_0 , U = pe^{Qt}, p(t+T) = p(t)\) - Bloch定理:\( [-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} A\cos(x) ] \psi(x) = \lambda \psi(x) \) 求解步骤:
(1). 找周期\(R\), \(H(x+R) = H(R)\) \(\Rightarrow\) \(\cos(x+R) = \cos(x)\) \(\Rightarrow\) \(R=2\pi\)
(2). \(|kR|\leq \pi\) \Rightarrow \(|k|\leq 1/2\)
(3). 写出Bloch波函数:\(U_k(x+R) = U_k(x) \) \(\Rightarrow\) \( U_k(x)=\sum_G c_k (G) e^{iGx} \) \(\Rightarrow\) \(G=n\in(-\infty,\infty)\)
(4). \(\psi_k(x) = \sum_G c_k(G)e^{i(G+k)x} \),代入薛定谔方程: 比较系数得
\(-\frac{\hbar^2}{2m} (n+k)^2 c_k(n) +\frac{A}{2}c_k(n-1) +\frac{1}{2} c_k(n+1) = \lambda c_k(n) \) (5). 写成矩阵形式,阶段大小\(N_c\)。 物理图像:与\(H\sum_{ij} t_{ij}c_i^\dagger c_j +h.c. +\mu_i c_i^\dagger c_i\)联系, \(\Rightarrow\) \(t_{ij} = A/2, \mu_i = \frac{\hbar^2}{2m}(i+k)^2 \)
其他结论:
(1). \(A\cos(x) \rightarrow A/2(e^{ix} + e^{-ix}) \) (2). \(A\sin(x) \rightarrow -iA/2(e^{ix} - e^{-ix}) \) (3). \(A_2\cos(2x) \rightarrow A_2/2(e^{i2x} + e^{-i2x}) \) (4). \(A_2\sin(2x) \rightarrow -iA_2/2(e^{i2x} - e^{-i2x}) \) - 作业15 根据以前步骤(1)计算\( [-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} A\cos(x) ] \psi(x) = \lambda \psi(x) \)本征值, (2).检查\(N_c\)多少时结果收敛, (3). 画出能带和Mathieus和Mathieuc比较。
- 作业16 找几个任意2维图形(矩形,圆,椭圆,操场,心形等),计算本征值以及波函数的空间分布。
- 2D差分方法,Quantum Scar
附:PPT - Exact Diagonalization(ED)步骤:
(1). 取一组正交完备的基矢 (2). 求矩阵元 (3). 得到矩阵对角化 - 两个粒子的ED:
(1). 两个费米子:基矢 \(c_n^\dagger c_m^\dagger |0\rangle, (n\neq m) \) \(\Rightarrow\) \(\Psi = \sum_{n_1,n_2} c_{n_1,n_2} | n_1 n_2 \rangle ,( n_2>n_1) \) \(\Rightarrow\) 一维化处理:\(\Psi = \sum_{\alpha} c_\alpha | \alpha \rangle \) 基态\(|GS\rangle = a_1^\dagger a_2^\dagger |0\rangle \), 基态能量一阶微扰\(E_g = E_1 + E_2 + \langle GS | V | GS\rangle\) (2). 两个玻色子:基矢 \( a_n^\dagger a_m^\dagger |0\rangle,(n\neq m) \) or \(\frac{1}{\sqrt{2}} (a_n^\dagger)^2 |0\rangle \) 基态\(|GS\rangle = \frac{1}{\sqrt{2}}(a_1^\dagger)^2 |0\rangle \), 基态能量一阶微扰\(E_g = 2E_1 + \langle GS | V | GS\rangle\) - ED总结:
(1). 适用单/多粒子 (2). 随粒子数Hilbert空间指数增长,小系统有一定参考价值,但无法做到热力学极限 (3). 可以计算基态和激发态,原则上没有算法误差,可以作为其他算法参考(Benchmark) - Lanczos method(WiKi)
- 作业17 求解一维单粒子体系\([-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V_0 \sin(qx)] \Psi(x) = E \Psi(x) \)参数自取。
- 作业18 两粒子系统\(H=H_0+V\),单粒子部分\(H_0 = -\frac{\hbar^2}{2m} (\frac{d^2}{dx^2} + \frac{d^2}{dy^2}) \),相互作用部分 \(V = g\delta(x-y)\)。任选Bose/Fermi子一种情况求解,并且当\(g\rightarrow 0\)和微扰结果比较。
- 平均场
(1). 无固定模式; (2). 常见问题有各种近似方法;(3). 往往用于求解相变问题和相边界。 (4). “多体~单体+自洽” (5). Idea: 算符\(AB\),\(A=\overline{A}+\delta A, B=\overline{B}+\delta B \) \(\Rightarrow\) \(AB = \overline{A} \overline{B} +\overline{A}\delta B + \overline{B}\delta A + \delta A \delta B \approx \overline{A}B+\overline{B}A-\overline{A}\overline{B} \),忽略了关联(涨落)项\(\delta A \delta B \) - Holstein–Primakoff(HP)变换,Spin系统和Bose系统之间的变换,设变换形式:
\( \left\{ \begin{array}{l} & S^\dagger = f(n) a^\dagger \\ & S^- = a f(n) \\ & S^z = g(n) \end{array} \right. \) 得到关系式: \( \left\{ \begin{array}{l} & f^2(n) = B_1+B_2n \\ & g(n) = A+n \end{array} \right. \) 确定\(A,B_1,B_2\)可以得到: \( \left\{ \begin{array}{l} & S_i^\dagger = (\sqrt{2S-n})a_i\\ & S_i^- = a_i^\dagger\sqrt{2S-n}\\ & S_i^z = S-n \end{array} \right. \) or \( \left\{ \begin{array}{l} & S_i^\dagger = a_i^\dagger (\sqrt{2S-n})\\ & S_i^- = \sqrt{2S-n}a_i\\ & S_i^z = n-S \end{array} \right. \) 其中\(n=a_i^\dagger a_i\) - 作业19 找到上面参数\(A,B_1,B_2\)之间的关系
- 作业20
(1). Schwinger Boson \( \left\{ \begin{array}{l} & S^\dagger = a^\dagger b\\ & S^- = b^\dagger a\\ & S^z = (a^\dagger a -b^\dagger b)/2 \end{array} \right. \) (a).证明\([S^\dagger,S^-] = 2 S_z\); (b). 计算\(S^2\); (c). 证明基矢\(| S,m \rangle =\frac{(a^\dagger)^{S+m}(b^\dagger)^{S-m}}{\sqrt{(S+m)!(S-m)!}} |0\rangle \)是算符\(S^2,S^z\)的本证态, 对应本征值\(S(S+1),m\),这里\(a^\dagger a+b^\dagger b = 2S\) (2). Schwinger Fermion同样计算(1)中的问题 (3). Dyson–Maleev变化 \( \left\{ \begin{array}{l} & J^\dagger = a\\ & J^- = a^\dagger (2S-n)\\ & J^z = S-a^\dagger a \end{array} \right. \) 计算\([J^\dagger,J^\dagger]\), \(J^2\) (4). \(\overrightarrow{J} = \frac{1}{2}a^\dagger \overrightarrow{\sigma} a\),证明\(\overrightarrow{J}\)和\(\overrightarrow{\sigma}\)有相同对易关系,计算\(J^2\)
- Jordan-Wigner变换
\( \left\{ \begin{array}{l} &S_{n}^{+} =c_{n}^{\dagger} \exp \left(i \pi \sum_{m=1}^{n-1} c_{m}^{\dagger} c_{m}\right) \\ &S_{n}^{-} =\exp \left(-i \pi \sum_{m=1}^{n-1} c_{m}^{+} c_{m}\right) c_{n} \\ &S_{n}^{z} =c_{n}^{\dagger} c_{n}-\frac{1}{2} \end{array} \right. \) - 应用铁磁,反铁磁系统
- 作业21 \(H = bS^\dagger + b^* S^- +b_z S^z\),代入HP变换\(S^\dagger = a^\dagger\sqrt{2S-a^\dagger a}, S^- = \sqrt{2S-a^\dagger a}a, S^z = a^\dagger a-S \),求解自由能。
- 作业22 计算\(\sum_{ij}(\Delta a_i^\dagger b_i^\dagger + \Delta b_i^\dagger a_j^\dagger +h.c.)\)的色散关系。
- 牛顿法求\(\overrightarrow{f}(\overrightarrow{x})=0\)
\(\overrightarrow{x}_{n+1} = \overrightarrow{x}_n -(J)^{-1} \overrightarrow{f}(\overrightarrow{x}_n) \), 其中\(J\)为Jacobian矩阵。 \(\overrightarrow{f}(\overrightarrow{x})=0\)与\((J)^{-1}\)无关,迭代中\((J)^{-1}\)的计算最为复杂。 - Broyden算法
基本思想:不计算\(J^{-1}\),用近似值代替,对最后的根无影响。 \(\mathbf{J}_{n}=\mathbf{J}_{n-1}+\frac{\Delta \mathbf{f}_{n}-\mathbf{J}_{n-1} \Delta \mathbf{x}_{n}}{\left\|\Delta \mathbf{x}_{n}\right\|^{2}} \Delta \mathbf{x}_{n}^{\mathrm{T}}\) \(\mathbf{J}_{n}^{-1}=\mathbf{J}_{n-1}^{-1}+\frac{\Delta \mathbf{x}_{n}-\mathbf{J}_{n-1}^{-1} \Delta \mathbf{f}_{n}}{\Delta \mathbf{x}_{n}^{\mathrm{T}} \mathbf{J}_{n-1}^{-1} \Delta \mathbf{f}_{n}} \Delta \mathbf{x}_{n}^{\mathrm{T}} \mathbf{J}_{n-1}^{-1}\) 只需得到\(J_1,J_1^{-1}\)可以利用上式迭代求\(J_n,J_n^{-1}\) - Dicke model: 附:Ref
(1)量子方法:\(H = \omega a^\dagger a +\omega_0 \sum_i \sigma_i^z + g/\sqrt{N} \sum(a^\dagger \sigma_i^- +h.c.)\), 其中\(N\)为原子数,\(g\)相互作用强度,定义: \( \left\{ \begin{array}{l} & J^z = \sum_i \sigma_i^z \\ & J^+ = \sum_i \sigma_i^+ \\ & J^- = \sum_i \sigma_i^- \end{array} \right. \) 得到\(H = \omega a^\dagger a +\omega_0 J^z + g/\sqrt{N} (J^\dagger a + h.c.)\) 利用近似HP变换\(J^+ \approx \sqrt{2N}b^\dagger \),得到 \(H = \omega a^\dagger a +\omega_0 b^\dagger b + \sqrt{2}g (a^\dagger b + h.c.) + \text{const} \), const\(=-N\omega_0\) \((a^\dagger,b^\dagger)\)\(\left( \begin{array}{l} & \omega \qquad \sqrt{2}g \\ &\sqrt{2}g \qquad \omega_0 \end{array} \right)\)\(\left( \begin{array}{l} & a \\ &b \end{array} \right)\) 得到\(E_{\pm} = \frac{\omega+\omega_0}{2}\pm \sqrt{\frac{(\omega-\omega_0)^2}{4} + 2g^2}\),相变点\(g_c = \sqrt{\frac{\omega\omega_0}{2} }\) (2)经典方法:\(H = \frac{p_1^2}{2m} + \frac{1}{2}m\omega^2 x_1^2 + \frac{p_2^2}{2m} + \frac{1}{2}m\omega_0^2 x_2^2 +\sqrt{2}g m \sqrt{\omega\omega_0} x_1x_2 + \sqrt{2}g \frac{p_1p_2}{m\sqrt{\omega\omega_0} }\) \(\dot{p_1} =-\frac{ \partial H}{ \partial x_1} = m\omega^2x_1 + \sqrt{2}gm\sqrt{\omega\omega_0}x_2 \) \(\dot{x_1} = \frac{ \partial H}{ \partial p_1} = \frac{p_1}{m} + \frac{\sqrt{2}gp_2}{m\sqrt{\omega\omega_0}}\) - 作业23 \(H = E_1 a_1^\dagger a + E_2 a_2^\dagger a_2 + U_1 n_1(n_1-1) + U_2n_2(n_2-1) + J(a_1^\dagger a_2 + h.c.)\)
方法一:(1). 利用Schwinger-Boson变换,用自旋算符\(J_x,J_y,J_z\)表示以上哈密顿量 (2). 在(1)结果上进行HP变换得到\(H(a,a^\dagger)\),求运动方程 (3). Josephson变换:\(a=e^{-i\theta}\sqrt{\rho}\), \(a^\dagger=\sqrt{\rho}e^{i\theta}\) 方法二:\(a_1 = e^{-i\theta_1}\sqrt{N_1}\), \(a_2 = e^{-i\theta_2}\sqrt{N_2}\) \(\Rightarrow\) \(i\dot{a_1} = [a_1,H]\),\(i\dot{a_2} = [a_2,H]\) (1). 推导 \(\left\{ \begin{array}{l} \dot{z} &=-\sqrt{1-z^{2}} \sin \phi \\ \dot{\phi} &=\Lambda z+\frac{z}{\sqrt{\left(1-z^{2}\right)}} \cos \phi+\Delta E \end{array} \right.\) 其中 \(\left\{ \begin{array}{l} z &=\frac{N_1-N_2}{N_1+N_2} \\ \phi & = \theta_2 -\theta_1 \end{array} \right.\) (2). 数值计算 (3). 比较两种方法
附:Ref
- 作业24 对于上文Dicke model经典方法,定义\(Y = (x_1,p_1,x_2,p_2)\), 求\(\dot{Y} = A Y\)
- \(\overrightarrow{f}(\overrightarrow{x})=0\) \(\Rightarrow\) \(x_{n+1}=x_n-J^{-1}f(x_n)\), where
\(J\) is Jacobi matrix
\(\Leftrightarrow\)
\(F=\sum_i f_i^2\) \(\Rightarrow\) \(F\rightarrow \min\) \(\Rightarrow\) \(\nabla F=0\) \(\Rightarrow\) \(x_{n+1} = =x_n - H^{-1} \nabla F\), where \(H\) is Hessian matrix - 算法:(1)steepest descent method(最速下降法), (2)conjugate gradient method(共轭梯度法)
- Bose-Hubbard model平均场
- Kuramoto model
\(\dot{\theta} = \omega_i + \frac{K}{N}\sum_j^N \sin(\theta_j - \theta_i)\) 序参量:\(Z=Re^{i\psi} = \frac{1}{N}\sum_j e^{i \theta_j}\) \(\Rightarrow\) \(\dot{\theta} = \omega_i - KR \sin(\theta_i - \psi)\),解 (1). 所以\(\dot{\theta_i}\)都不一样,长时间平均\(|Z|\sim \frac{1}{\sqrt{N}}\) (2). 所有振子同频率\(\dot{\theta_i} = \overline{\omega}\) \(\Rightarrow\) 稳态解:\(\dot{\theta_i} = \omega_i-KR \sin[\theta_i(0)-\theta(0)]\), 条件:\(|\frac{\omega_i-\overline{\omega}}{KR}| \leq 1\) 同步时的\(\theta_i(0)\)分布:\(P_s(\varphi)=g(\overline{\omega} + KR \sin \varphi) KR \cos \varphi\) 临界点\(K_c = \frac{2}{\pi g(\overline{\omega})}\) - 作业25 Kuramoto model \(\dot{\theta} = \omega_i + \frac{K}{N}\sum_j^N \sin(\theta_j - \theta_i)\) 数值求解,\(N=200\sim 500\)左右。
- 混沌
(1). Lorentza吸引子,(2). 极限环 连续方程:Lorentza吸引子;离散:Logistic map Ref: PPT - Kicked rotor: \(H = \frac{p^2}{2}+k \cos q \sum_n \delta(t-nT)\)
Standord map eq: \(p_{n+1}^- = p_n^- +k\sin q_n, \quad q_{n+1} = q_n+p_{n+1}^-\) - 作业26 求Standard map相图,扫描k
- 作业27 \(H = \frac{p^2}{2} + k\cos q \sum_n [\delta(t-nT) + \delta(t-nT+T_0)]\)
(1). 求出standard map方程(eq1) (2). 画出相图(fig1) Ref: PhysRevLett.99.234101
- Bogoliubov-De-Gennes方程
- 相互作用与平均场
(1) Coulomb Interaction: \(V(\overrightarrow{x}-\overrightarrow{y})\) (2) Contact Interaction: \(g\delta(\overrightarrow{x}-\overrightarrow{y})\) (3) Spinless: \(\sum_{k_1k_2 q}V_q \psi_{k_1+q}^{\dagger}\psi_{k_1-q}^{\dagger}\psi_{k_2}\psi_{k_1}\)Spin: \(\sum_{k_1k_2 q}V_q \psi_{k_1+q,\uparrow}^{\dagger}\psi_{k_1-q,\downarrow}^{\dagger}\psi_{k_2,\downarrow}\psi_{k_1,\uparrow}\) (4) Hatree项: \(\psi_{k_1+q,\uparrow}^{\dagger}\psi_{k_1,\uparrow}\psi_{k_1-q,\downarrow}^{\dagger}\psi_{k_2,\downarrow}\) Fock项: \(-\psi_{k_1+q,\uparrow}^{\dagger}\psi_{k_2,\downarrow} \psi_{k_1-q,\downarrow}^{\dagger}\psi_{k_1,\uparrow}\) (5) \(g>0\): 排斥相互作用, Hatree项主要 (6) \(g<0\): 吸引相互作用, Fock项主要 \(H = \sum_{k\sigma}\varepsilon_{k\sigma}\psi_{k\sigma}^{\dagger}\psi_{k\sigma}+\Delta \psi_{k\uparrow}^\dagger\psi_{k\downarrow}^\dagger +h.c.\) 基态能量: \(E_g=\sum_{k}(\varepsilon_k-\sqrt{\varepsilon_k^2+|\Delta|^2})-\frac{|\Delta|^2}{g}\) 求解: \(\frac{\partial E_g}{\partial \Delta^*}=0 \quad \Rightarrow \quad -\frac{\Delta}{g}-\sum_k \frac{\Delta}{\sqrt{\varepsilon_k^2+|\Delta|^2}} =0 \)
- Nonlinear equation, PPT
- (1) Gross–Pitaevskii(GP)方程
(2) Fast Fourier Method (3) Imaginary Time Method PPT , Ref: Numerical solution of the Gross–Pitaevskii equation GP方程代码 - 作业28 已知\(H = T(x)+V(x), T = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\), Time-evolution equation, \(\psi(x, t+\Delta t)=e^{-i \Delta t H / \hbar} \psi(x, t)\), 证明: \(e^{-i \Delta t H / \hbar} \approx e^{-i \Delta t V /(2 \hbar)} e^{-i \Delta t T / \hbar} e^{-i \Delta t V / 2 \hbar} \psi\) holds the error \(\left(\mathcal{O}\left(\Delta t^{3}\right)\right)\)
- 作业29 已知Time-Dependent Gross-Pitaevskii Equation
\(i \hbar \frac{\partial}{\partial t} \psi(\mathbf{x}, t)=\left[-\frac{\hbar^{2}}{2 m} \nabla^{2}+V(\mathbf{x}, t)+g|\psi(\mathbf{x}, t)|^{2}\right] \psi(\mathbf{x}, t)\), 其中\(V(x) = \frac{1}{2}m\omega^2(x^2-a^2)\),数值求解基态能量和波函数。
- BCS
(1) k-space: \(H = \sum_{k\sigma}\varepsilon_k c_{k\sigma}^\dagger c_{k\sigma} + \Delta c_{k\uparrow}^\dagger c_{-k\downarrow}^\dagger +h.c.\) (2) r-space: \(H = -t\sum_{i\sigma} c_{i\sigma}^\dagger c_{i+1,\sigma} + \Delta c_{k\uparrow}^\dagger c_{-k\downarrow}^\dagger +h.c.\) 写基矢,对应矩阵形式 - 作业30 (1) Spinless model(Kitaev model)
\(H = \sum_i ( -tc_i^\dagger c_{i+1} + \Delta c_i^\dagger c_{i+1}^\dagger + h.c. ) + \sum_i c_i^\dagger c_i\) 取值\(L=100,t=1\),扫描\(\mu,\Delta\),画出能谱和相图。 (2) s-wave SC model \(H = -t\sum_{i,\sigma} (c_{i,\sigma}^\dagger c_{i+1,\sigma} +h.c. ) +\Delta \sum_i ( c_{i,\uparrow}^\dagger c_{i,\downarrow}^\dagger + h.c.) + \mu \sum_{i,\sigma} c_{i,\sigma}^\dagger c_{i,\sigma} + h \sum_i (c_{i,\uparrow}^\dagger c_{i,\uparrow}- c_{i,\downarrow}^\dagger c_{i,\downarrow})\) 取值\(L=100,t=1\),讨论问题自定。 (3) SOC-s-wave SC model \(H = -t\sum_{i,\sigma} (c_{i,\sigma}^\dagger c_{i+1,\sigma} +h.c. ) +\Delta \sum_i ( c_{i,\uparrow}^\dagger c_{i,\downarrow}^\dagger + h.c.) + \mu \sum_{i,\sigma} c_{i,\sigma}^\dagger c_{i,\sigma} + h \sum_i (c_{i,\uparrow}^\dagger c_{i,\uparrow}- c_{i,\downarrow}^\dagger c_{i,\downarrow}) +\lambda \sum_{i} ( c_{i,\uparrow}^\dagger c_{i+1,\downarrow} - c_{i,\downarrow}^\dagger c_{i+1,\uparrow } +h.c.) \) 取值\(L=100,t=1\),画相图。
- BdG方程对称性: particle-hole symmetry
\(c=\sigma_x k\), \(cHc^{-1} = -H\) - Anderson localization
(1) 1维,2维没有extended state到localized state转变,任意小的无序都为 localized state (2) 3维度存在extended state到localized state转变,\(W < W_c\)为 extended state,\(W > W_c\)为 localized state (3) 1D model: \(H = -t\sum_i[c_i^\dagger c_{i+1} + h.c.] + \sum_i V_i c_i^\dagger c_i\)。其中:\(V_i \in [-W,W]\)的均匀分布。 (4) 转移矩阵,参考Hoffmann的书章节 Transfer-Matrix Methods and Finite-Size Scaling for Disordered Systems (5) QR分解:\(A = QR\), 满足\(Q^\dagger Q = 1\). \(T_nT_{n-1}...T_2T_1 = Q_n R_n R_{n-1} R_2R_1\) - Aubry-André (AA) model: \(H = -t\sum_i (c_i^\dagger c_{i+1}+h.c.) + \sum_{i}V \cos(qi)c_i^\dagger c_i\), \(q\)为无理数。\(V=-2t\)时,傅里叶变换一致\(H_k=H_i\),对偶。相边界:\(V=-2t\)
- 作业31 讨论 AA model 性质:
(1) 用严格对角化方法证明扩展态到局域态转变在\(V=-2t\), 取\(L=1000,q=\frac{\sqrt{5}-1}{2}\), 计算inverse participation (IPR), IPR=\(\sum_i |P_i|^2\) (2) 推导AA model 的对偶关系:\(V=-2t\) (3) 用转移矩阵方法计算\(\xi (E)\)的值,与(1)得到的边界比较。
- 有限元
- 随机过程
(1) 中心极限定理,大数定理 (2) Einstein扩散方程 Einstein paper \(\frac{D}{2} \frac{\partial ^2 p}{\partial t^2} = \frac{\partial p}{\partial t}\) (3) 郎之万方程 \(m \dot{\overrightarrow{v}} =\overrightarrow{F} -\eta \overrightarrow{v} +\xi\) (4) Einstein关系: \(D = 2\eta k_B T\) - 作业32 用投针法计算\(\pi\)的值。求\(\pi\)分别近似到3.14, 3.1415, 3.14159时所需要的总投针次数\(N\)
- 随机行走
\(n\)步以后,在\(l\)处的位置: \(P(l) = \frac{1}{2^n} C_n^{n/2+l/2} =\frac{n!}{2^n (n/2+l/2)!(n/2-l/2)!} \) - 随机过程
- 物理中:\(m \dot{x}=-\dot{v}(x)-r\dot{x}+\xi\)
数学中:\(dx=\mu dt+\sigma dw\), \(dw=\xi dt\) - Itô's lemma (Wiki)
- 作业33 Mathematica计算随机行走\(P(l)\)
- 作业34 Brownian motion: \(\dot{v}=-rv+\xi\)
\(v(t)-v(0)=\int_0^t (-\gamma v+\xi)dt\), 数值:\(v_n = v_{n-1}-\gamma v_{n-1} \delta t +\xi_{n-1} \delta t\), \(\langle \xi_n^2\rangle = \frac{1}{\delta t}\) 和严格结果对比(每一时刻平均值,方差)
- caldeira-leggett model (Wiki)
振子与振子之间的相互作用 \(H = \frac{P^2}{2M}+V(X)+\sum_j^N [\frac{p_j^2}{2m_j}+\frac{1}{2}m_j\omega_j^2(x_j-\frac{C_j}{m_j\omega_j^2}X)^2]\) 定义:\(\gamma(t)=\sum_j \frac{1}{M}\frac{C_j^2}{m_j\omega_j^2}\cos(\omega_j t)\) \(F_L = \sum_j C_j [x_j(t_0)\cos(\omega_j(t-t_0))+\frac{p_j}{m_j\omega_j}\sin(\omega_j(t-t_0))]\) \(\Rightarrow\) \(M \ddot{x}+M \int_{t_0}^t \gamma(t-t^\prime)\frac{dx(t^\prime)}{dt}dt^\prime = -M\gamma(t-t_0)x(t_0)+F_L-V^\prime(x)\) 极端情况:\(\gamma(t)=\gamma\delta(t)\) \(\Rightarrow\) \(M\ddot{x}+\frac{M}{2}\gamma \dot{x}(t)=F_L-V^\prime(x)\) - 谱函数:\(J(\omega)=\frac{\pi}{2}\sum_j \frac{C_j^2}{m_j\omega_j^2}\delta(\omega-\omega_j)\)
- 作业35 \(\overline{F_L}=\sum_j C_j \overline{x_j} = 0\), \(\overline{x_j}=\int x_je^{-\beta}(\frac{p_j^2}{2m_j}+\frac{1}{2}m_j\omega_j^2x_j^2)dx_j\),
计算\(\overline{F_L(t)F_L(t+\tau)} = Mk_BT \gamma(\tau) \doteq Mk_BT\delta(\tau)\) - 作业36 1个粒子和N个振子相互作用,求该粒子的运动。N=1000, \(\omega_j,m_j\)随机分布
- 随机力\(F_L=\sum_i(m_i \omega_i^2 \alpha_i q_i)\)
(1). \(\langle F_L \rangle = 0\) (2). \(\langle F_L^2\rangle \propto k_BT\) - 量子CL model
\(b_i = \sqrt{\frac{m_i \omega_i}{2}}q_i + \frac{i p_i}{\sqrt{2m_i\omega_i}}\) \(b_i = \sqrt{\frac{m_i \omega_i}{2}}q_i - \frac{i p_i}{\sqrt{2m_i\omega_i}}\) \(\Rightarrow\) \(F_L = \sum_i \frac{m_i\omega_i^2 \alpha_i}{\sqrt{2m_i\omega_i}}(b_i+b_i^\dagger)\) \(\langle (b_ib_i^\dagger)^2 \rangle = (2n_i+1)\) \(\Rightarrow\) \(\langle F_L^2 \rangle \approx \sum_i m_i \omega_i^2 \alpha_i^2 k_BT \propto k_BT\) - Langevin方程
\(\left\{\begin{aligned} & m \ddot{x} = -V^\prime(x) -\gamma \dot{x} +\sum_i \eta_i (b_i+b_i^\dagger) \\ & V(x) = \frac{1}{2}m \omega^2 x^2 \end{aligned} \right.\) \( \left\{\begin{aligned} & a = \sqrt{\frac{m\omega}{2}} x +\frac{ip}{\sqrt{2m\omega}}\\ & a^\dagger = \sqrt{\frac{m\omega}{2}} x- \frac{ip}{\sqrt{2m\omega}} \end{aligned} \right. \) \(\Rightarrow\) \(\left\{\begin{aligned} & i \dot{a} = \omega a -i \frac{\gamma}{m}a +\xi \\ & \xi = \sum_i \sqrt{\frac{2}{m\omega}} \eta_i b_i \end{aligned} \right.\) - 耗散/退相干
\(t=0\), 纯态\(\rho_0 =|\psi\rangle \langle \psi|\), 热浴\(\rho_B\) 初始:\(\rho(t=0) = \rho_0 \otimes \rho_B \), 演化:\(\rho(t)=U\rho(t=0)U^\dagger\), 约化密度矩阵:\(\rho_s(t)=Tr_B(\rho(t)) = Tr_B(U\rho_0\otimes \rho_B U^\dagger)\) 若\(\rho_B = |0 \rangle \langle 0|\),则: (1). \(\rho_s(t) = \sum_i \langle i|U|0\rangle \rho_0 \langle 0 |U^\dagger|i\rangle = \sum_i M_i \rho_0 M_i^\dagger\), 其中\(M_i = \langle i|U|0\rangle \) \(\sum_i M_i^\dagger M_i = 1\) (2). \(\rho_s = \rho_s^\dagger\) (3). \(Tr(\rho_s) = 1\) (4). 正定的:\(\langle \psi |\rho_0 |\psi \rangle = \langle \psi | \rho_0 | \psi \rangle \geqslant 0\) - 作业37 若\(\rho_B = \frac{1}{Z} \sum_\alpha e^{-\beta \varepsilon_\alpha |\alpha \rangle \langle \alpha |}\),证明以上4点性质。
- Kraus表示
\( \rho_s(t) = \sum_i M_i \rho_s M_i^\dagger \equiv \$(\rho) \) \( \rho_s(t+dt) = \sum_i M_i (dt) \rho_s(t) M_i^\dagger (dt) = \rho_s(t) + \frac{d \rho_s}{dt} (dt) \) 假设\(M_0 = 1+ Gdt\), \( M_i = Li \sqrt{dt}\) 设\(G = A+iB\), \(G^\dagger=A-iB\). \(A=-\frac{1}{2}\sum_i Li^\dagger Li\) 总结:\(\frac{d \rho_s}{dt} = L(\rho_s)\), \(L(\rho_s) = -i[H,\rho_s] + \sum_i D_i(\rho_s)\), \(D_i(\rho_s) = \sum_i (Li \rho_s Li^\dagger -\frac{1}{2}\rho_s Li^\dagger Li -\frac{1}{2}Li^\dagger Li \rho_s)\)
好处:(1)无需求\(M_i(t)\), (2)定义几个简单的Operator可以了解环境贡献, (3)无法用定性方法,可以用实验方法确定, (4)\(\sum M_i^\dagger(t) M_i(t)=1\),\(Li\)无限定,自动满足 - 作业38 Spin-1/2
\(\frac{d \rho}{dt} = -i [H,\rho] + \gamma(1-f) D(\sigma_-) + \gamma f D(\sigma_+)\), \(D(L) = L \rho L^\dagger - \frac{1}{2}\rho L^\dagger L -\frac{1}{2}L^\dagger L \rho\), \(H = \frac{\Omega}{2}\sigma_z\), Hilbert空间\(|\uparrow\rangle, |\downarrow\rangle\). 求解\(\rho_{\uparrow\uparrow},\rho_{\downarrow\downarrow}, \rho_{\uparrow\downarrow}, \rho_{\downarrow\uparrow}\)演化方程,画图。
数值:\(\frac{d}{dt}\langle n| \rho_s |m \rangle = \frac{d}{dt}\rho_{n+1}\)
- Lindblad Equation
(1)Spin model, \(\gamma\)与\(f\)的物理意义:
\(f\)是平衡时的分配,\(\gamma\)是delay rate (2) Boson model \(H_s = \omega (a^\dagger a +\frac{1}{2})\), \(i \dot{\rho} = [H_s,\rho] +\gamma_1 D(a) + \gamma_2 D(a^\dagger)=[H_s,\rho]+ \gamma_1(a^\dagger \rho a -\frac{1}{2}\rho a a^\dagger -\frac{1}{2}a a^\dagger \rho) + \gamma_2 (a \rho a^\dagger -\frac{1}{2}\rho a^\dagger a -\frac{1}{2}a^\dagger a \rho)\) 求解:Hilbert空间\(\{|0\rangle,|1\rangle,...\}\), 长时间平衡\(\overline{n} = \frac{1}{e^{\beta\omega}-1}\) 对角化稳态:\(\dot{\rho}_{nn}=0\), 引入\(\rho_{nn}=\rho_n\) \(\gamma_1(n \rho_{n-1}-(n+1)\rho_n ) \gamma_2 ((n+1)\rho_{n+1} - n \rho_n) = 0\) \(\gamma_1/\gamma_2 = e^{-\beta \omega}\) for \(\forall n\) \(\Rightarrow\) \(\gamma_1 = \gamma\overline{n}, \gamma_1 = \gamma(\overline{n}+1) \) (3) Fermion model \(D(f^\dagger), D(f), D(n)\) \(D(n)= (n\rho n -\frac{1}{2}\rho n^2 -\frac{1}{2}n^2\rho ) \equiv n\rho n -\frac{1}{2}\rho n -\frac{1}{2}n \rho \) 平衡意义下:\(\rho(t+dt) = \rho(t) + i\rho A^\dagger dt -iA \rho dt +\sum_i Li \rho Li^\dagger dt\) Let:\(A = H-\frac{i}{2}\sum_i Li^\dagger Li\) - Vec函数
(1) 定义 \(\rho = \sum_{ij} |i\rangle \langle j|\) (2) \(tr(A^\dagger B) = \sum_{ik} A_{ki}^* B_{ki}\) = Vec(A)^\dagger Vec(B) (3) \(Vec(ABC) = \sum A_{ij} B_{jm} C_{mn} |i\rangle |n \rangle\) = (C^T \bigotimes A)Vec(B) (4) 定义:\(V = Vec(\rho)\) \(\Rightarrow\) \(i \dot{V} = L V\) - 作业39 Boson model 求解\(\rho\)的对角和非对角元
- 作业40 Fermion model
讨论\(H_s = w f^\dagger f\), \(\gamma_1 D(f) + \gamma_2 D(f^\dagger) + \gamma_3 D(f^\dagger f)\), \(\gamma_1,\gamma_2\gamma_3\)任取,Hilbert空间0,1 or \(\uparrow,\downarrow\)
- 相干态
\(|\alpha\rangle = \sum_{n=0}^{\infty} e^{-|\alpha|^2/2}\frac{\alpha^n}{\sqrt{n!}}|n\rangle, \quad \alpha\in \mathcal{C}\)
\(a|\alpha\rangle = \alpha |\alpha\rangle\), \(a^\dagger|\alpha\rangle = (\frac{\partial}{\partial \alpha}+\frac{1}{2}\alpha^*)|\alpha\rangle\) \(\langle\alpha|a^\dagger = \alpha^* \langle\alpha|\), \(\langle\alpha|a = (\frac{\partial}{\partial\alpha^*}+\frac{1}{2}\alpha)\langle\alpha| \) \(\frac{\partial p}{\partial t} = \frac{\gamma_+}{2} \frac{\partial}{\partial\alpha} [\alpha p\alpha + c.c.] + \gamma_- \frac{\partial^2}{\partial\alpha^*\partial\alpha}p\) - MC simulation
重要采样:\(W(x)=\frac{P(x)}{f(x)}\), \(f(x) = \frac{1}{L}\sum_i \delta(x-x_i)\), \(\int_a^b P(x)dx = \frac{1}{L}\sum_iW(x_i)\) Metropolis算法: (1) 细致平衡\(\frac{dp_a}{dt} = \sum_B P_{B} W_{B\rightarrow A} - \sum_A P_{A} W_{A\rightarrow B} =0 \) (2) 配分函数:\(Z=Tr(e^{\beta H})\) \(P_B W_{B\rightarrow A} = P_A W_{A\rightarrow B} \) \(\Rightarrow\) \(e^{-\beta E_A}W_{A\rightarrow B} = e^{-\beta E_B}W_{B\rightarrow A} \) \(\Rightarrow\) \(W_{A\rightarrow B} = \min (1,e^{-\beta \Delta E})\), \(\Delta E = E_B-E_A\)