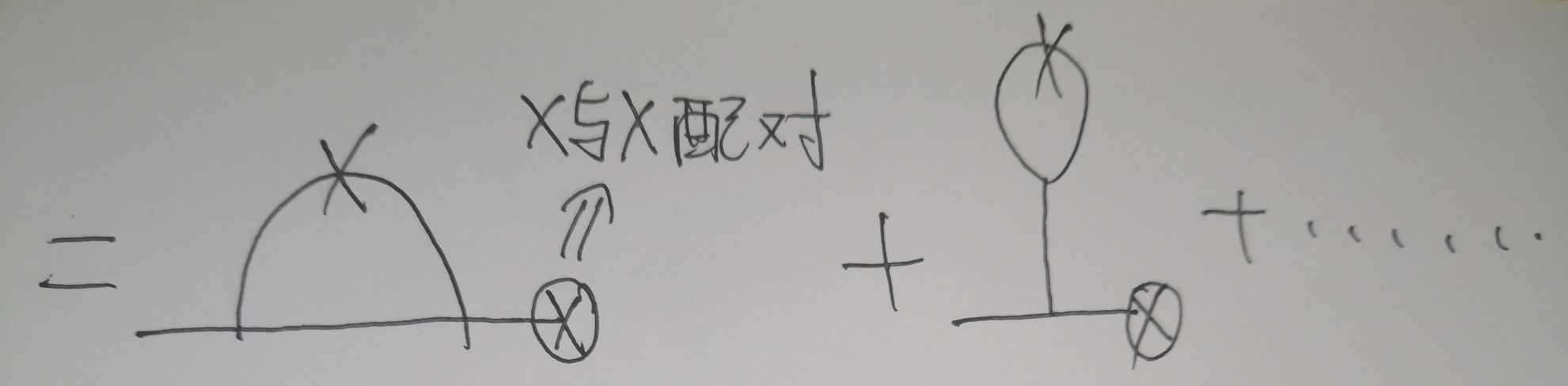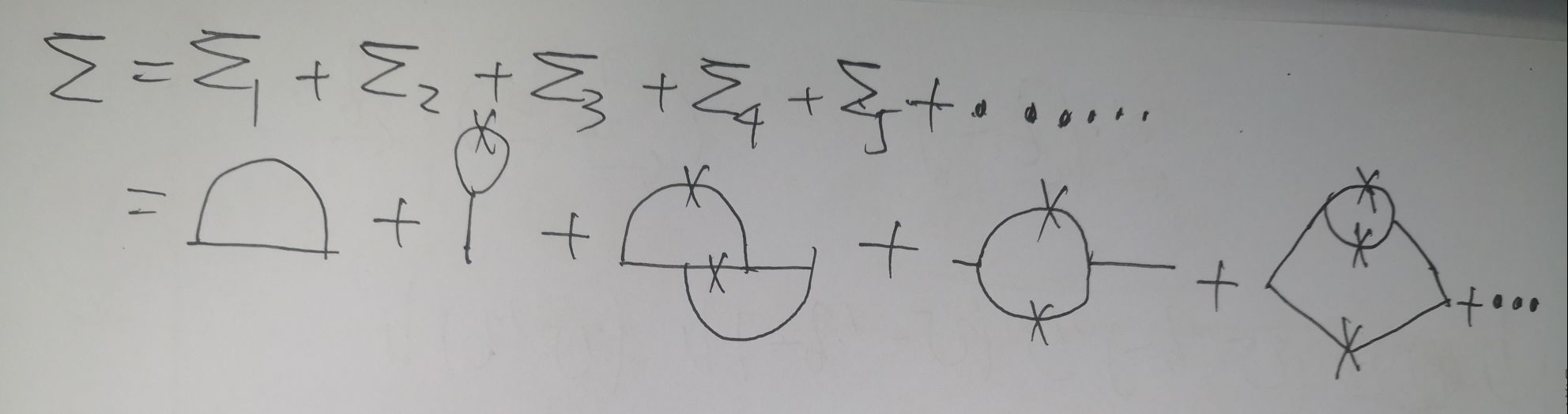返回上级菜单

5.23 周一

1. 参考：
   1. 中国科学技术大学刘国柱老师，量子多体理论讲义，电子与杂质的相互作用
   2. Uryszek_PRB_2022
   3. Feynman，量子力学与路径积分，其中的随机力的路径积分
2. 对无序的平均转换为对配分函数Z的平均，相似点都是路径积分做平均\(\langle X\rangle=\frac{\int D\phi Xe^{-S}}{\int D\phi e^{-S}}=\int D\phi XP(\phi)=\frac{1}{N}\sum_iG(\xi_i)\),\(P(\phi)=\frac{e^{-S}}{Z}\)
   这可以处理多体相关问题、相变相关问题
   对无序的平均可以用第12周课程主页讲解的Replica Trick方法来做
3. 统计力学中非平衡系统的传播子\(\int D\phi e^{-\beta H}\sim\int D\phi e^{-\beta(k^2+m^2)\phi_k^*\phi_k}\)，\(\langle\phi_k^*\phi_k\rangle=\frac{1}{\beta(k^2+m^2)}\)
4. 后续老师讲解的部分全部可以参考我第13周课程主页：引领大家阅读参考文献：Parisi，吴咏时，不用固定规范的微扰论(中文版)，这里我不再赘述
   学生笔记
   学生笔记2
   学生笔记3

5.26 周四

1. 参考：
   1. KPZ方程原始论文
   2. 张翼成：我与诺贝尔物理学奖获得者Parisi教授的故事
   3. 诺奖得主Parisi在中科院理论物理所的一次合作，返朴
   4. Parisi，吴咏时，不用固定规范的微扰论(英文版)
   5. Parisi，吴咏时，不用固定规范的微扰论(中文版)(备注：中文版部分物理符号很不清晰)
   6. Medina,Hwa,Kardar,Zhang,1989 PRA:Burgers equation with correlated noise:renormalization group analysis and applications to directed polymers and interface growth
   7. 中国科学技术大学刘国柱老师，量子多体理论讲义，电子与杂质的相互作用
   8. 中国科学技术大学刘国柱老师，量子多体理论讲义，顶角修正
2. YiCheng Zhang1989年文章比1986年文章多了新东西：讨论了correlated disorder，将原先假定的\(\langle\eta(x,t)\eta(x',t')\rangle=2D\delta(x-x')\delta(t-t')\)换成了\(\langle\eta(x,t)\eta(x',t')\rangle=2Df_1(x-y)f_2(t-t')\)
   或者也可以是\((\partial\delta(x-x'))\delta(t-t')\)，傅里叶变换得\(\langle\eta(k,\omega)\eta(k',\omega')\rangle=2D\delta(k+k')\delta(\omega+\omega')*ik\),这将导致新的色散关系
3. 今日主要任务：解方程\(\dot{h}(x,t)=\nu\triangledown^2h+\eta+\frac{g}{2}(\triangledown h)^2\)
   动量空间\(h(x,t)=\frac{1}{V}\sum_{k\omega}e^{i(\vec{k}\cdot\vec{x}-\omega t)}h(k,\omega)\)
   傅里叶变换得\(-i\omega h(k,\omega)=-\nu k^2h(k,\omega)+\eta(k,\omega)+\frac{g}{2}\sum_{q,\Omega}(iq)(i(k-q))h(q,\Omega)h(k-q,\omega-\Omega)\)
   \(\rightarrow(\nu k^2-i\omega)h(k,\omega)=\eta(k,\omega)-\frac{g}{2}\sum_{q\Omega}q(k-q)h(q,\Omega)h(k-q,\omega-\Omega)\)
   定义\(G_0(k,\omega)=\frac{1}{\nu k^2-i\omega}\)，于是有\(h(k,\omega)=G_0(k,\omega)\eta(k,\omega)-\frac{g}{2}G_0(k,\omega)\sum_{q\Omega}q(k-q)h(q,\Omega)h(k-q,\omega-\Omega)\equiv G(k,\omega)\eta(k,\omega)\)，费曼图如下所示

   

   

   
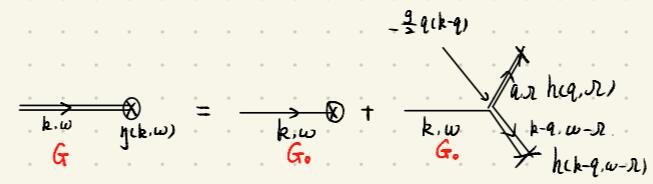
   \(\langle h(k,\omega)\eta(-k,-\omega)\rangle=G(k,\omega)D(k,\omega)\)，相当于上面的图中一个\(\times\)与外场的\(\eta(-k,-\omega)\)对应的\(\times\)配对，剩余的偶数个\(\times\)互相配对，费曼图如下所示

   

   
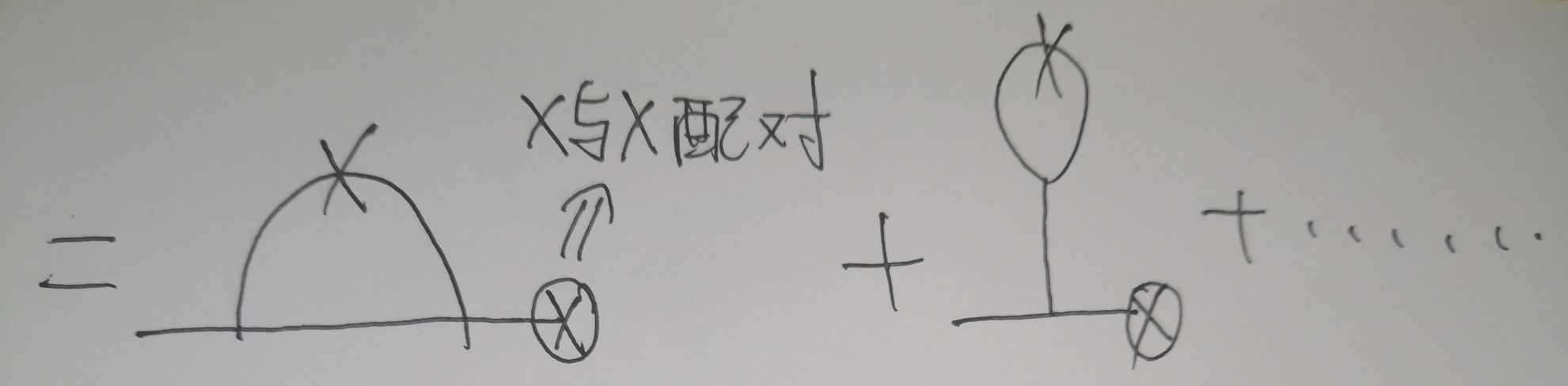
   考虑一阶近似后结果(这里只考虑了上图最左侧的Feynman图，这里只是为了说明其中蕴含的物理而已)：
   \(G(k,\omega)=G_0(k,\omega)-4(-\frac{g}{2})^2G_0^2(k,\omega)\int\int d\Omega d^dq\frac{1}{(2\pi)^d}\vec{q}\cdot(\vec{k}-\vec{q})\vec{q}\cdot\vec{k}G_0(\vec{k}-\vec{q},\omega-\Omega)G_0(\vec{q},\Omega)G_0(-\vec{q},-\Omega)2D(q,\Omega)\)
   考虑该费曼图的高阶修正，根据Dyson方程，如下图所示：

   

   
   \(G=\frac{G_0}{1-\varSigma G_0}\),\(\varSigma\)如下图所示：

   

   
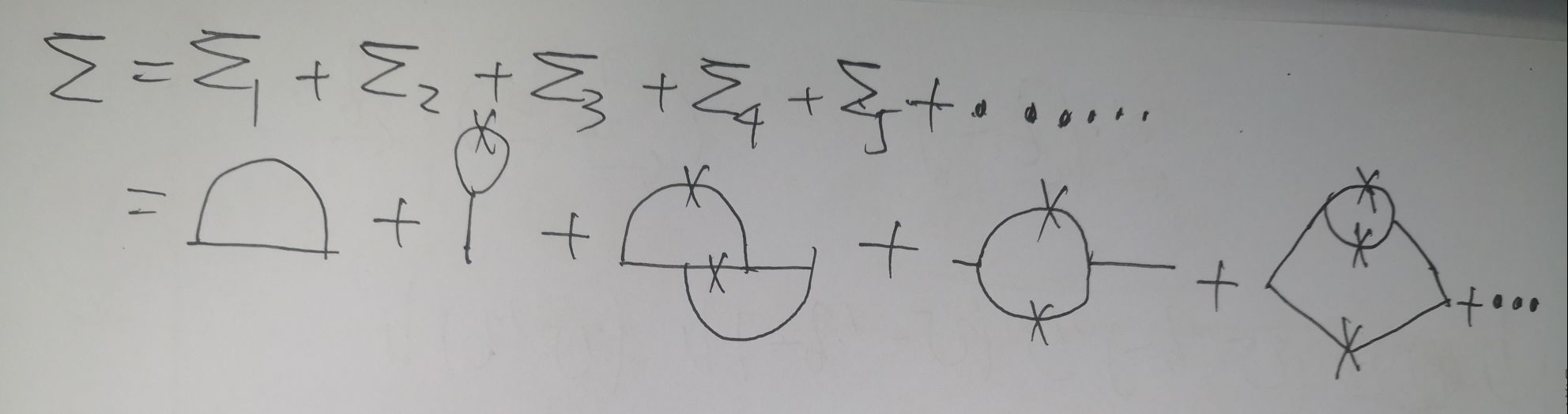
   总体费曼图修正可以列表如下所示：

   

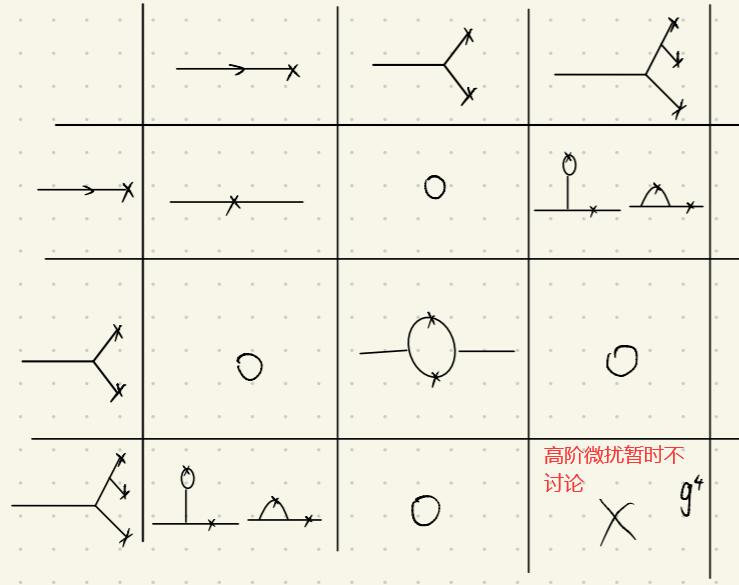
4. 注，以上考虑都没考虑顶角修正，具体可参考中国科学技术大学刘国柱老师，量子多体理论讲义，顶角修正

   

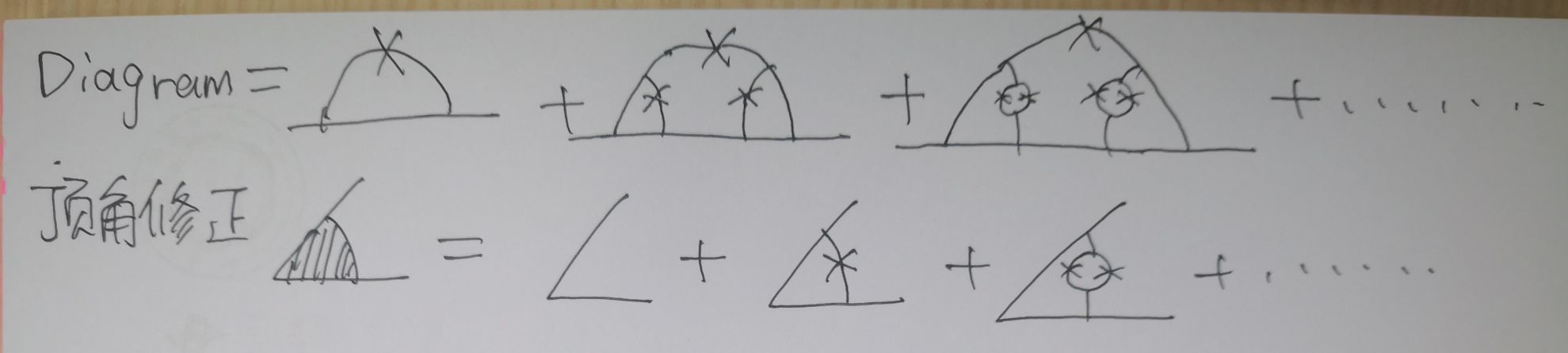
5. KPZ相变原始论文中Eq5直接给出了展开到低阶项的部分重整化顶角修正、腿修正等结果
   学生笔记
   学生笔记2
   学生笔记3