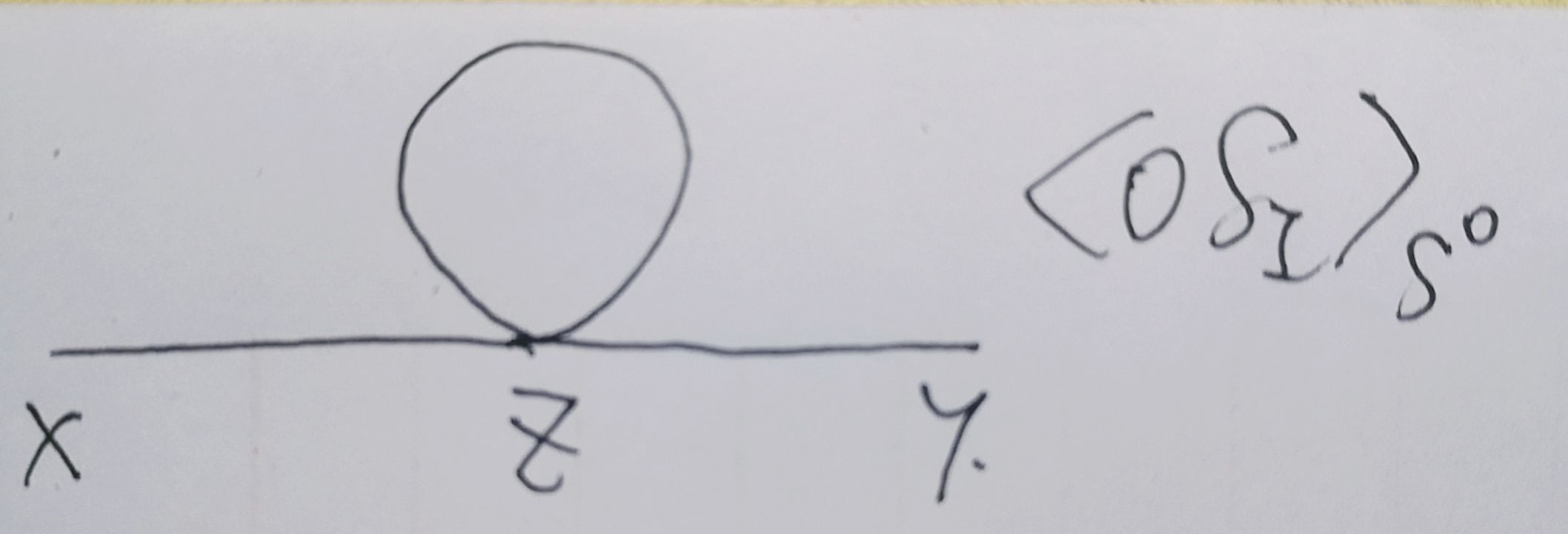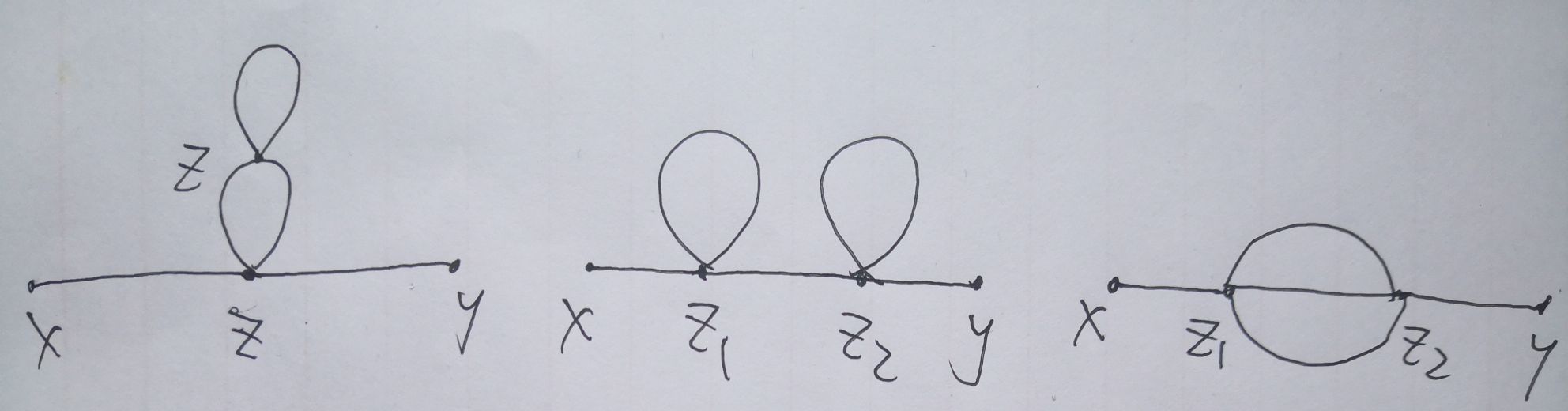返回上级菜单

3.14 周一

1. 继续讲解\(\phi^4\)理论的计算
   \(L=L_0+L_I,L_0=\frac{1}{2}(\partial_{\mu}\phi)^2-\frac{m^2}{2}\phi^2,L_I=-\frac{\lambda}{4!}\phi^4\)
   \(\langle O\rangle_{S_0}=\frac{\int D\phi e^{iS_0}O}{\int D\phi e^{iS_0}},\langle O\rangle=\frac{\int D\phi e^{iS}O}{\int D\phi e^{iS}}\)
   上节课讲解了集团展开的方法来求解\(Z=\langle e^{tX}\rangle=e^{\Omega}\)
   上节课给了连通定理的一个式子的严格证明：只有连通图有贡献的严格证明，严格证明了以下式子：
   \(\langle O\rangle_{S_0+S_I}=\frac{\langle Oe^{-S_I}\rangle_{S_0}}{\langle e^{-S_I}\rangle_{S_0}}\)
   其中\(\langle OS_I^n\rangle_0=\langle OS_I^n\rangle_{S^0}\),c为连通图
   上节课算出自由情况下\(S_0=\frac{1}{V}\sum_k(k^2-m^2)\phi^*(k)\phi(k),\langle \phi(x)\phi(y)\rangle=\frac{1}{V^2}\sum_k\langle \phi^*(k)\phi(k)\rangle=\frac{1}{V}\sum_k\frac{ie^{ik\cdot(x-y)}}{k^2-m^2}\)
   注：Peskin书第二章讲了太多时序算子T，以及超前格林函数、推迟格林函数、时序格林函数，这里不要求掌握
   一般情况下计算费曼图采用时序格林函数。高量Sakurai书中散射理论用的是推迟格林函数。对时序格林函数，其积分解析延拓到复平面，格林函数修正为\(\langle\phi(x)\phi(y)\rangle=\frac{1}{V}\sum_k\frac{ie^{ik\cdot(x-y)}}{k^2-m^2+i\epsilon}\)
   微扰论费曼图计算：\(\langle OS_I\rangle_{S_0}=-\frac{\lambda}{4!}\int dz\frac{\int D\phi\phi(x)\phi(y)\phi^4(z)e^{iS_0}}{\int D\phi e^{iS_0}}\)只有一种连通的费曼图，即一种配对形式，如下图所示，每一条连接的线条都是一个配对，表示\(\langle\phi(首端点)\phi(尾端点)\rangle\)，一个费曼图有几条线就要将这几条线都乘起来，最后要乘以简并度

   

   
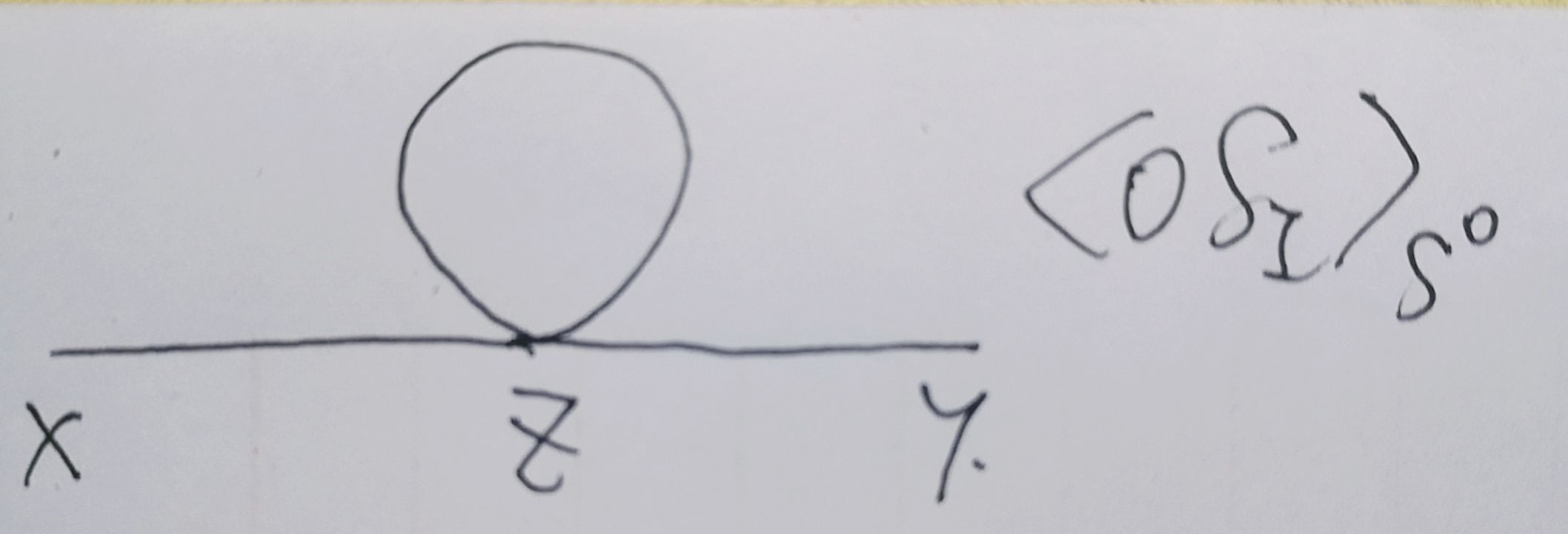
   简并度计算：画一个叉叉，交点为z点，表示\(\phi^4(z)\)，再画一个x点和一个y点，不同的连接方式有12种
   计算公式如下：
   定义\(g(x-y)=\langle\phi(x)\phi(y)\rangle_{S_0+S_I},g_0(x-y)=\langle\phi(x)\phi(y)\rangle_{S_0}\)
   根据Feynman图计算得：\(g(x-y)=g_0(x-y)-\int\frac{i\lambda}{2}g_0(x-z)g_0(z-z)g_0(z-y)d^4z\)
   \(g(k)=g_0(k)-\frac{i\lambda}{2}g_0(k)g_0(0)g_0(k)\)，很像卷积运算
   最后积分下来结果存在发散，结果\(\frac{1}{V}\frac{V}{(2\pi)^d}\int dk_0d\vec{k}\frac{i}{k_0^2-\vec{k}^2-m^2+i\epsilon}\propto\bigwedge^2\)
2. 质量修正Dyson方程：人为定义\(g(x-y)=\frac{i}{V}\sum_k\frac{e^{ik\cdot(x-y)}}{k^2-m^2+i\epsilon},g_0(x-y)=\frac{i}{V}\sum_k\frac{e^{ik\cdot(x-y)}}{k^2-m_0^2+i\epsilon}\)
   \(\rightarrow g(k)=\frac{1}{k^2-m_0^2-\varSigma+i\epsilon},g_0(k)=\frac{1}{k^2-m_0^2+i\epsilon}\)
   \(\rightarrow m^2=m_0^2+\varSigma,g=g_0+g_0\varSigma g\)，可看作\(m^2\)为修正后质量(实验观测值)，\(m_0^2\)为自由质量
3. 要计算相互作用系数\(\lambda\phi^4\)中的\(\lambda\)修正，需要计算\(\langle\phi(p_1)\phi(p_2)\phi(p_3)\phi(p_4)\rangle_{S_0+S_I}=\int dz\langle\frac{\int D\phi e^{iS_0}\phi^4(z)O}{\int D\phi e^{iS_0}}\rangle_{S_0}^c\)
   一阶修正费曼图如下图所示

   

   
   其费曼图计算公式正比于\(\frac{1}{V}\sum_k(\frac{1}{k^2-m^2+i\epsilon})^2\)，积分最终结果为\(ln\bigwedge\)发散
   完整的相互作用系数\(\lambda\)修正见Shankar书第14章(后面几次课讲)
4. 计算二阶修正，\(\langle \phi(x)\phi(y)S_I^2\rangle_{S^0}\)，费曼图如下图所示：

   

   
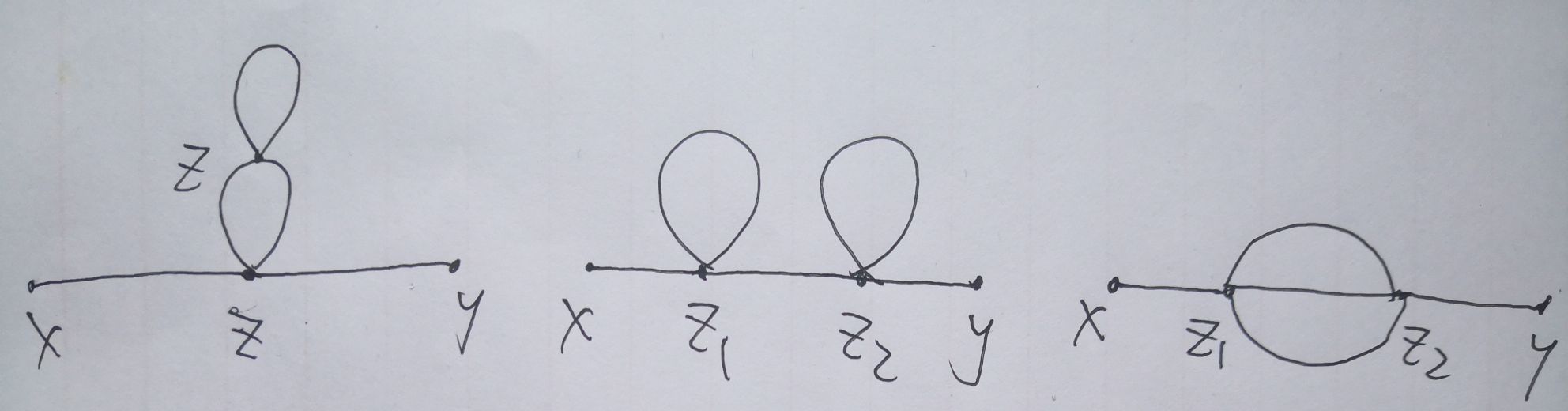
   前两幅图Feynman图计算的表达式为\(\propto\lambda^2(\frac{1}{V}\sum_k\frac{1}{k^2-m^2+i\epsilon})\frac{1}\sum_{k'}(\frac{1}{k'^2-m^2+i\epsilon})^2\)，发散程度\(\propto\bigwedge^2ln\bigwedge\)
   第三幅图很多文献都算不出来，计算结果一般为\(\frac{1}{p^2-m_0^2}\rightarrow\frac{1}{(1+\delta)p^2-m_0^2}\)
5. 本节没有讲的东西：T算子、超前格林函数、推迟格林函数、Peskin书第二部分一堆复杂技巧(维度正规化、Feynman参数化，粒子物理教授们要讲一个月才能讲明白)
6. 微扰论理解方式：\(H=\frac{p^2}{2m}+\frac{1}{2}m\omega^2x^2+\frac{1}{4}\lambda x^4\)，本征能量为\(E=\hbar\omega(n+\frac{1}{2})+\frac{\lambda}{4}\langle n|x^4|n\rangle+\cdot\cdot\cdot\)
   处理\(\phi^4\)理论本质上也是这种思想，用微扰展开，但是微扰展开结果有发散
7. 一种处理方法：\(L=\frac{1}{2}(\partial_{\mu}\phi)^2-\frac{m_0^2}{2}\phi^2-\frac{\lambda_0}{4!}\phi^4=L_R(m_R,\lambda_R)+\triangle L(m_0,\lambda_0,m_R,\lambda_R)\)，其中\(L_R(m_R,\lambda_R)\)为重整化观测值，下标R表示重整化，\(\triangle L\)要抵消\(L_R\)发散
   \(\infty-\infty=\)任何一个有限值，靠实验确定能标\(\mu<<\bigwedge\)和观测值\(\lambda_R\)，重整化步骤：
   \(\phi=\sqrt{Z}\phi_R\rightarrow L=\frac{1}{2}(\partial_{\mu}\phi_R)^2-\frac{m_R^2}{2}\phi_R^2-\frac{\lambda_R}{4!}\phi_R^4+\frac{1}{2}\delta Z(\partial_{\mu}\phi_R)^2-\frac{\delta m^2}{2}\phi_R^2-\frac{\delta\lambda}{4!}\phi_R^4\)，将后面三项视为微扰，用量子力学微扰论方法求解，确定参数\(\delta Z,\delta m^2,\delta\lambda\)使一阶微扰和二阶微扰能量为0即可
   这种思路换成\(\phi^3,\phi^5\)等更复杂形式就不知道怎么做了，千万别纠结细节
8. 下节课：Wilson重整化群，绝大部分模型都可用Wilson重整化群方法求解
   学生笔记
   学生笔记2
   学生笔记3

3.17 周四

1. 本课程讲义见3.17课程讲义
2. 维度正规化方法(这是计算细节，本课程不要求掌握。)
   维度正规化方法参考1
   维度正规化方法参考2,Peskin247-252页
   Addendum to Wilson's theory of critical phenomena and Callan-Symanzik equations in 4−ε dimensions
   Wilson, Fisher, Critical Exponents in 3.99 Dimensions
   学生笔记
   学生笔记2
   学生笔记3