返回上级菜单

2.28 周二

1. 场的路径积分初步
   包含：boson场路径积分、fermion场路径积分(Grassmann代数)、规范场路径积分、自旋场路径积分(今日只讲了一点点boson场，后续课程会选择一部分讲，不讲完)
2. 今日讲解内容参考：
   1. azee书1.2节、1.3节
   2. altland书对路径积分的讲解，102-105页
3. 附注：所有场路径积分参考文献(只做参考，本课程只要求掌握老师讲解到的部分，其余均不做要求)
   1. 场路径积分统一公式
   2. Gauss积分常见公式
   3. 费米子路径积分(Grassmann代数)和玻色子路径积分，Nagaosa37-44页
   4. 自旋场路径积分(与Berry相有关),Nagaosa47-50页
   5. 自旋场路径积分(与Berry相有关),文小刚书34-38页
   6. 相干态路径积分,文小刚书14-15页
   7. 阿贝尔规范场路径积分(靠Fadeev-Popov Method消除发散),peskin书294-297页
   8. 阿贝尔规范场路径积分(靠fadeev-popov Method消除发散)，srednicki书343-344页
4. 今日首先讲解：Boson场的路径积分。首先给引理：Gauss积分
   Fubini公式：\(\int dxe^{-Ax^2}=\sqrt{\frac{\pi}{A}}\rightarrow\int dxdye^{-A(x^2+y^2)}=\int 2\pi\rho d\rho e^{-A\rho^2}=\frac{\pi}{A}\)
   \(\int dxe^{-Ax^2+Jx}=\sqrt{\frac{\pi}{A}}e^{J^2/(4A)}\)
   \(\int e^{-Ax^2}x^{2n}dx=\int e^{-Ax^2}\sum_{m=0}^{+\infty}\frac{(Jx)^m}{m!}=\sqrt{\frac{\pi}{A}}e^{J^2/(4A)}\rightarrow\langle x^{2n}\rangle=\frac{(2n)!}{n!2^{2n}}\frac{1}{A^n} \)
   意义：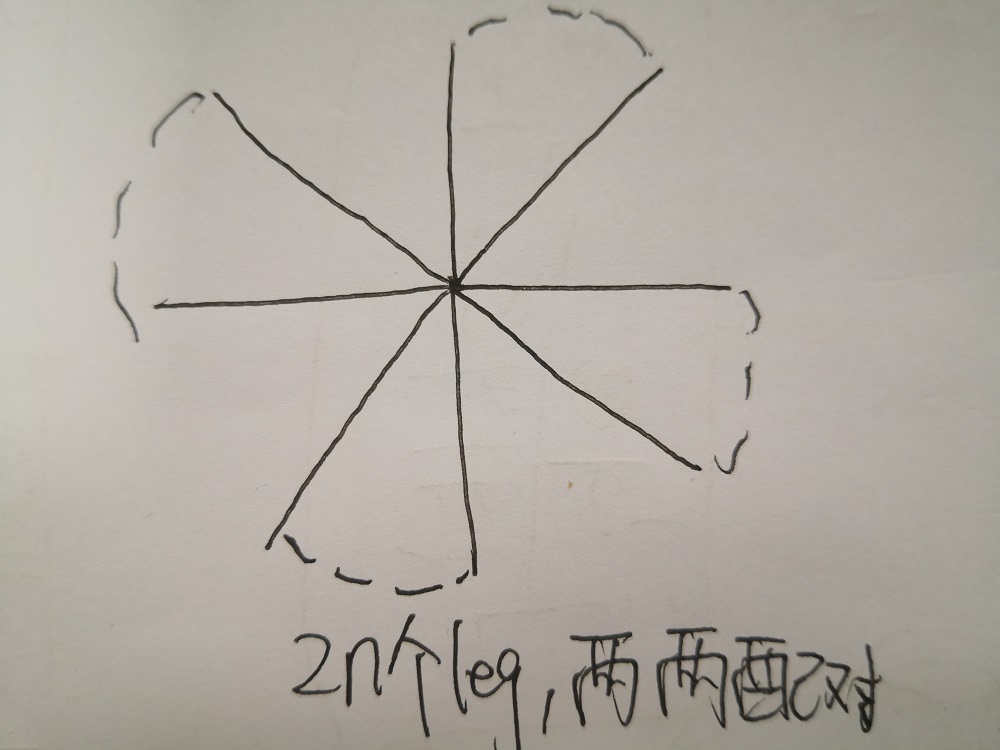

   

   
   2n个leg两两配对，考虑全同性，种类有\(\frac{1}{2^n}C_{2n}^2C_{2n-2}^2C_{2n-4}^2\cdot\cdot\cdot C_2^2=\frac{(2n)!}{n!2^{2n}}\)
5. 将Gauss积分推广到复数场情况和多分量情况
   \(x=Oy\)时，\(\int dx_1dx_2\cdot\cdot\cdot dx_n=det(O)dy_1dy_2\cdot\cdot\cdot dy_N\rightarrow\int DXe^{-\frac{1}{2}x^TAx}=\int Dye^{-\frac{1}{2}\sum_i\lambda_iy_i^2}=\frac{(2\pi)^{n/2}}{\sqrt{det(A)}}\)
   \(\langle x_ix_j\rangle=\frac{\frac{\partial}{\partial J_i}\frac{\partial}{\partial J_j}\int dx_1\cdot\cdot\cdot dx_Ne^{-\frac{1}{2}x^TAx+J^Tx}}{\int dx_1\cdot\cdot\cdot dx_Ne^{-\frac{1}{2}x^TAx}}|_{J=0}=\frac{\partial}{\partial J_i}\frac{\partial}{\partial J_j}e^{J^TA^{-1}J/2}|_{J=0}=\frac{1}{2}(A^{-1})_{ij}\)
   推广到复数场\(\frac{\int dzd\bar{z}z\bar{z}e^{-\frac{1}{2}A\bar{z}z}}{\int dzd\bar{z}e^{-\frac{1}{2}A\bar{z}z}}=\frac{\int dxdye^{-\frac{1}{2}A(x^2+y^2)}(x^2+y^2)}{\int dxdye^{-\frac{1}{2}A(x^2+y^2)}}\)
   
6. 作业1 :
   加入弱多体相互作用后积分形式为\(\int dxe^{-\frac{1}{2}Ax^2-\frac{\lambda}{4!}x^4}\)，将\(e^{-\frac{\lambda}{4!}x^4}\)微扰展开后，分析收敛性(比如永远收敛，或者几阶后不收敛)，
   学生笔记
   学生笔记2
   学生笔记3

3.3 周四

1. 场论中发散问题初步
   场论要直接面对发散问题，多体理论不直接面对发散问题
2. 2D \(\delta-potentional\)
3. Casimir force
4. 精细结构劈裂\(g_s=2.002\cdot\cdot\cdot\)

1. 温习：
   场拉格朗日量\(L=(\frac{\partial\phi}{\partial t})^2-v^2(\frac{\partial\phi}{\partial x})^2-m^2\phi^2-\frac{\lambda}{4!}\phi^4\)
   \(\phi\)意义：坐标/振动的大小
   路径积分：\(Z=\int D\phi e^{iS},S=\int Ld\vec{x}dt\),\(D\phi=d\phi(x_1)d\phi(x_2)\cdot\cdot\cdot d\phi(x_N)\)
   真实模拟路径积分：可用MonteCarlo方法，参考丁泽军教授计算物理主页，
   变换到动量空间中，\(\prod_id\phi(x_i)\rightarrow J\prod_kd\phi(k)\)，绝大多数情况下J为常数，只有场论中少数情况\(J=J(k,\phi(k))\)，也因此\(\langle Q\rangle=\frac{\int P(x)Qdx}{\int P(x)dx}\)与J无关
   不要记忆高斯积分恒等式，需要时就查表！你容易弄混\(\frac{A}{2},2A\)，表见：场路径积分统一公式
2. 今日讲解内容参考：
   1. Casimir力原始论文
   2. 卡西米尔力，苗兵
   3. Regularization methods for delta-function potential in two-dimensional quantum mechanics
   4. An analytical example of renormalization in 2D quantum mechanics
   5. a hint of renormalization
   6. anomalies in quantum mechanics:the \(1/r^2\) potential
   7. Casimir effect and vacuum fluctuations.Trang T.Nguyen
3. 发散无处不在
   比如说库仑力\(V=e^2/r\)在大尺度下永远正确，但在\(r<10^{-6}nm\)是否正确？我们回顾电磁学，如果我们接受电磁场的观点，根据能量密度求总能量，则\(\int dV\frac{1}{2}\epsilon_0E^2\propto\int\frac{1}{r^4}d^3r\propto\frac{1}{r}|_0^{\infty}\)， 那么能量是无限大的。因此我们认为经典电磁学下电荷有一定大小，\(a\sim10^{-16}nm\)，则可以消除能量发散\(\epsilon\propto\frac{1}{r}|_a^{\infty}\)
4. 2D情况下的重整化：求2D\(\delta(x)\)势下的本征能量，参考资料
   \(H=\frac{p^2}{2m}+\lambda\delta(x),H\psi=E\psi\)
   \(\psi=\sum_kc_ke^{i\vec{k}\cdot\vec{x}},\delta(x)=A\sum_ke^{ik\cdot x}\)
   \(1=A\sum_k\int e^{ik\cdot r}dr=A\sum_k[\int_0^{\infty}e^{ikx-\epsilon x}dx+\int_{-\infty}^0e^{ikx+\epsilon x}dx]=\frac{AL}{2\pi}\int dk\frac{2\epsilon}{\epsilon^2+k^2}\rightarrow A=\frac{1}{L}\)
   \(\rightarrow\sum_k\frac{\hbar^2k^2}{2m}c_k+\frac{\lambda}{L}\sum_qc_{k-q}=\sum_kEc_k\)
   由于\(\sum_qc_{k-q}=\psi(0)\)，故\(c_k=\frac{\psi(0)\lambda}{L^2}\frac{1}{E-\frac{\hbar^2k^2}{2m}}\)
   \(\psi(0)=\sum_kc_k=\frac{\psi(0)\lambda}{L^2}\sum_k\frac{1}{E-\frac{\hbar^2k^2}{2m}}\)
   可得本征值方程\(1=\frac{\lambda}{L^2}\sum_k\frac{1}{E-\frac{\hbar^2k^2}{2m}}=\frac{\lambda}{L^2}\Omega^D\int k^Ddk\frac{1}{E-\frac{\hbar^2k^2}{2m}}\)
   对于1D\(\delta\)函数而言该积分是收敛的，但是对于2D、3D情况而言积分是发散的，因此对于这种积分，就要像假设电荷有大小一样，对积分取截断
   我们考虑2D情况下的截断\(1=\lambda\frac{1}{2\pi}\int_0^{\bigwedge}\frac{kdk}{E-\frac{\hbar^2k^2}{2m}}\)
   求得能量本征值为\(E=-\frac{\hbar^2\bigwedge^2}{2m}e^{\frac{4\pi}{\lambda_0(\bigwedge)}},\lambda_0=\frac{2m\lambda}{\hbar^2}\)，一般情况下理论值应与实验值符合
   等能曲线\(dE=0\rightarrow\beta(\lambda_0)=\frac{d\lambda_0}{dln\bigwedge}=-\frac{\alpha\lambda_0^2}{2\pi}<0\)
   renormalization flow如图所示：

   

   
   当把束缚势能换一下，有\(H=\frac{p^2}{2m}-\lambda\delta(x),H\psi=E\psi\)
   renormalization flow如下图所示：

   

   
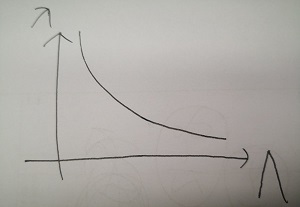
   实际情况下较大的\(\bigwedge\)不可达不可测，只能达到实验的低能能标\(\mu<<\bigwedge\)，测得\(\lambda_R\)，有公式\(E=-\frac{\hbar^2\mu^2}{2m}e^{-\frac{4\pi}{\lambda_R}}\)
5. Casimir力
   电磁场量子化后为玻色谐振子，能量为\(H=\sum_k\hbar\omega_k(a_k^{\dagger}a_k+\frac{1}{2})\)，真空零点能(基态能为\(H=\sum_k\frac{\hbar\omega_k}{2}\))，Sakurai书7.8节
   两个二维无限大平板，间距为d，则总能量为\(E=\frac{\hbar c}{2}\sum_{n,k_x,k_y}\sqrt{(\frac{n\pi}{d})^2+k_x^2+k_y^2}\)，本质上是发散结果，要像处理电荷有尺寸一样处理掉这个发散
   过去的物理：有限的物理；现在的物理：无限-无限=有限的物理
   初始我们考虑整个空间是1D空间情形，我们来消除发散，方法一参考卡西米尔力，苗兵
   \(E=\frac{1}{2}\sum_{n=1}^{\infty}\hbar c\frac{n\pi}{d}\rightarrow E=\frac{1}{2}\sum_{n=1}^{\infty}\hbar c\frac{n\pi}{d}e^{-\epsilon n}=\frac{\hbar cd}{2\pi\epsilon^2}-\frac{\pi\hbar c}{24d}+O(a^2)\)
   根据无限-无限=有限，去掉上个式子第一项(无限项)，得\(E=-\frac{\pi\hbar c}{24d},F=-\frac{\partial E}{\partial d}=-\frac{\hbar c\pi}{24d^2}\)
   注：额外计算整个1D真空能，\(E_0=\frac{\hbar cL}{2}\int_{-\infty}^{\infty}\frac{dk}{2\pi}|k|=\frac{\hbar cL}{2\pi}\int_0^{\infty}kdk\)，做同样的正规化
   \(E=\frac{\hbar cL}{2\pi}\int_0^{\infty}dkke^{-\epsilon k}=\frac{\hbar cL}{2\pi\epsilon^2}\)，这蛮有意思的，说明被减掉的背景是无限大的真空本身固有能量
   方法二参考卡西米尔力，苗兵，直接利用黎曼zeta函数公式\(1+2+3+\cdot\cdot\cdot=-\frac{1}{12}\)
   开始讨论3D情况，参考卡西米尔力，苗兵，直接利用黎曼zeta函数公式\(1^3+2^3+\cdot\cdot\cdot=\frac{1}{120}\)
   得到3D情况下单位面积Casimier能量\(\frac{E_0^C(a)}{A}=-\frac{\pi^2\hbar c}{720a^3}\)，压强为\(P(a)=-\frac{\pi^2\hbar c}{240a^4}\)
   方法三参考Casimir力原始论文，Sakurai书7.8节
   真空零点能\(E=\hbar c\frac{L^2}{\pi^2}\int_0^{\infty}\int_0^{\infty}\frac{1}{2}\sqrt{k_x^2+k_y^2}+\sum_{n=1}^{\infty}\sqrt{n^2\frac{\pi^2}{a^2}+k_x^2+k_y^2}dk_xdk_y\)
   去掉真空自由能后也就消除了发散，能量表达式为\(E=\hbar c\frac{A}{2\pi^2}\int_0^{\infty}\int_0^{\infty}\sqrt{k_x^2+k_y^2}dk_xdk_y+\hbar c\frac{A}{\pi^2}\int_{0}^{\infty}\int_0^{\infty}\sum_{n=1}^{\infty}\sqrt{n^2\frac{\pi^2}{a^2}+k_x^2+k_y^2}dk_xdk_y-\frac{A\hbar cL}{\pi^3}\int_0^{\infty}dk_x\int_0^{\infty}dk_y\int_0^{\infty}dk_z\sqrt{k_x^2+k_y^2+k_z^2}\)
   欧拉麦克劳林公式\(\frac{F(0)}{2}+\sum_{i=1}^{\infty}F(i)-\int_0^{\infty}F(x)dx=-\frac{1}{12}F'(0)+\frac{1}{720}F'''(0)\)
   进行换元和用mathematica算积分可得\(E=-\frac{\pi^2\hbar cA}{720d^3}\)，受力满足\(F=\frac{1}{A}(-\frac{dU}{dd})=-\frac{\pi^2\hbar c}{240d^4}\)
   Casimir原始论文最后一句话好玩叙述：Although the effect is small,an experimental confirmation seems not unfeasable and might be of a certain interest。
   学生笔记
   学生笔记2
   学生笔记3