返回上级菜单

4.11 周一

1. 1D情况下\(\psi=e^{i\Phi}\)证明：
2. Shankar第17章
3. Sine-Gordon Model重整化参考文献：
   1. 文小刚书中文版3.3.12节
   2. Shankar 18.4.2节
4. XY模型与BKT相变参考：
   1. Naoto Nagaosa,Quantum Field Theory in Condensed Matter Physics,page 68-70(最基本最简单的图像)
   2. 上面书page70页过后还计算了关联函数等等性质，计算过程较复杂
   3. BKT相变与Sine-Gordon Model联系：Naoto Nagaosa,Quantum Field Theory in Condensed Matter Physics，从page68开始可一直用各种技巧，一直推导到Eq3.3.32为Sine-Gordon Model，然后利用Sine-Gordon Model的重整化推出相变临界值
   4. BKT相变原始文献
   5. kosterlitz-nobellecture
   6. BKT相变实验进展
   ，前面用最简洁语言介绍了基本理论，里面Eq22为高等固体物理第四章准长程序
5. BKT相变实验进展：
6. BKT相变实验文章1
7. BKT相变实验文章2
8. BKT相变实验文章3
9. 龚老师总结
10. 在量子霍尔效应(QHE)前已经有很多超越朗道相变理论的现象，如Anderson局域化、BKT相变，BKT相变是无穷阶相变
11. Sine-Gordon Model:\(L=\frac{1}{2}(\partial_x\phi)^2+\frac{1}{2}(\partial_t\phi)^2+Acos\beta\phi,\partial_t^2\phi=\partial_x^2\phi+A\beta sin\beta\phi\)
    Sine-Gordon Model是经典问题，是少数的可解Model，可以给出孤子解
    变换坐标\((x,t)\rightarrow(x,y)\)为BKT相变形式
12. Sine-Gordon Model的重整化
    能标变换：\(Z=\int D\phi e^{-S},S=\int dtdx[\frac{1}{2}(\partial_t\phi)^2+\frac{1}{2}(\partial_x\phi)^2+Acos\beta\phi]\)
    作标度分析，\(\int dtdx(\partial_t\phi)^2=\int dt'dx'(\partial_{t'}\phi'(x'))^2\)，取\(t'=\lambda t,x'=\lambda x\)，则有\(\phi'(\lambda x,\lambda t)=\phi(x,t)\)
    不同的表述形式：\(\int dydx Acos(\beta\phi)=\int dydx y\wedge^2cos\beta\phi=\int dtdx\frac{y}{a^2}cos\beta\phi\)，其中A是动量平方量纲，可表述为\(y\wedge^2\)或\(\frac{y}{a^2}\)形式，其中\(\wedge=\frac{1}{\pi a}\)
    \(Z=\int D\phi e^{-\int\frac{1}{2}(\partial\phi)^2+Acos\beta\phi}=\int D\phi_{<}D\phi_{>}e^{-(S_{<}+S_{>}+\delta S)}\)
    第一种表示形式\(S_{<}=\int dx\frac{1}{2}(\partial\phi_{<})^2+Acos(\beta\phi_{<}),S_{>}=\int dx\frac{1}{2}(\partial\phi_{>})^2,\delta S=\int Acos[\beta(\phi_{<}+\phi_{>})]-Acos(\beta\phi_{<})\)
    第二种表示形式\(S_{<}=\int dx\frac{1}{2}(\partial\phi_{<})^2,S_{>}=\int dx\frac{1}{2}(\partial\phi_{>})^2,\delta S=\int Acos[\beta(\phi_{<}+\phi_{>})]\)
    这两种形式在\(b\rightarrow1^-\)上是等价的。我们进行泰勒展开\(cos[\beta(\phi_{<}+\phi_{>})]-Acos(\beta\phi_{<})=cos(\beta\phi_{<})(-\frac{\beta^2}{2}\phi_{>}^2)-\beta sin(\beta\phi_{<})\phi_{>}\)
    \(Z=\int D\phi_{<}e^{-S_{<}}\langle e^{-\delta S}\rangle_{S_{>}}\int D\phi_{>}e^{-S_{>}}\)，其中\(\int D\phi_{>}e^{-S_{>}},\langle e^{-\delta S}\rangle_{S_{>}}=e^{-\langle\delta S\rangle_{>}+\frac{1}{2}\langle\delta S^2\rangle_{>}^c}\)
    一般当一阶连通项\(\langle\delta S\rangle_{>}\neq0\)时，可忽略二阶连通项\(\frac{1}{2}\langle\delta S^2\rangle_{>}^c\)，故
    \(\langle\delta S\rangle_{>}=-\frac{A\beta^2}{2}\int dxcos(\beta\phi_{<})\langle\phi_{>}^2\rangle=-\frac{A\beta^2}{2}\int dxcos(\beta\phi_{<})\frac{1-b}{2\pi}\)
    故有\(Z=\int D\phi_{<}e^{-\int dx\frac{1}{2}(\partial\phi_{<})^2+A(1-\frac{1-b}{4\pi}\beta^2)cos(\beta\phi_{<})}\)
    做Rescaling，\(k\rightarrow\frac{1}{b}k,A\rightarrow\frac{1}{b^2}A\)，Rescaling过后有
    \(Z=\int D\phi e^{-\int dx\frac{1}{2}(\partial\phi)^2+Ab^{-2}(1-\frac{1-b}{4\pi}\beta^2)cos\beta\phi}\)
    \(A(b)=Ab^{-2}(1-\frac{1-b}{4\pi}\beta^2),b=1-dl\rightarrow A(b)=A+A(2-\frac{\beta^2}{4\pi})dl=A-\frac{dA}{dln\wedge}dl\)
    \(A(\wedge)\propto e^{(\frac{\beta^2}{4\pi}-2)ln\wedge}\)

    

    
    
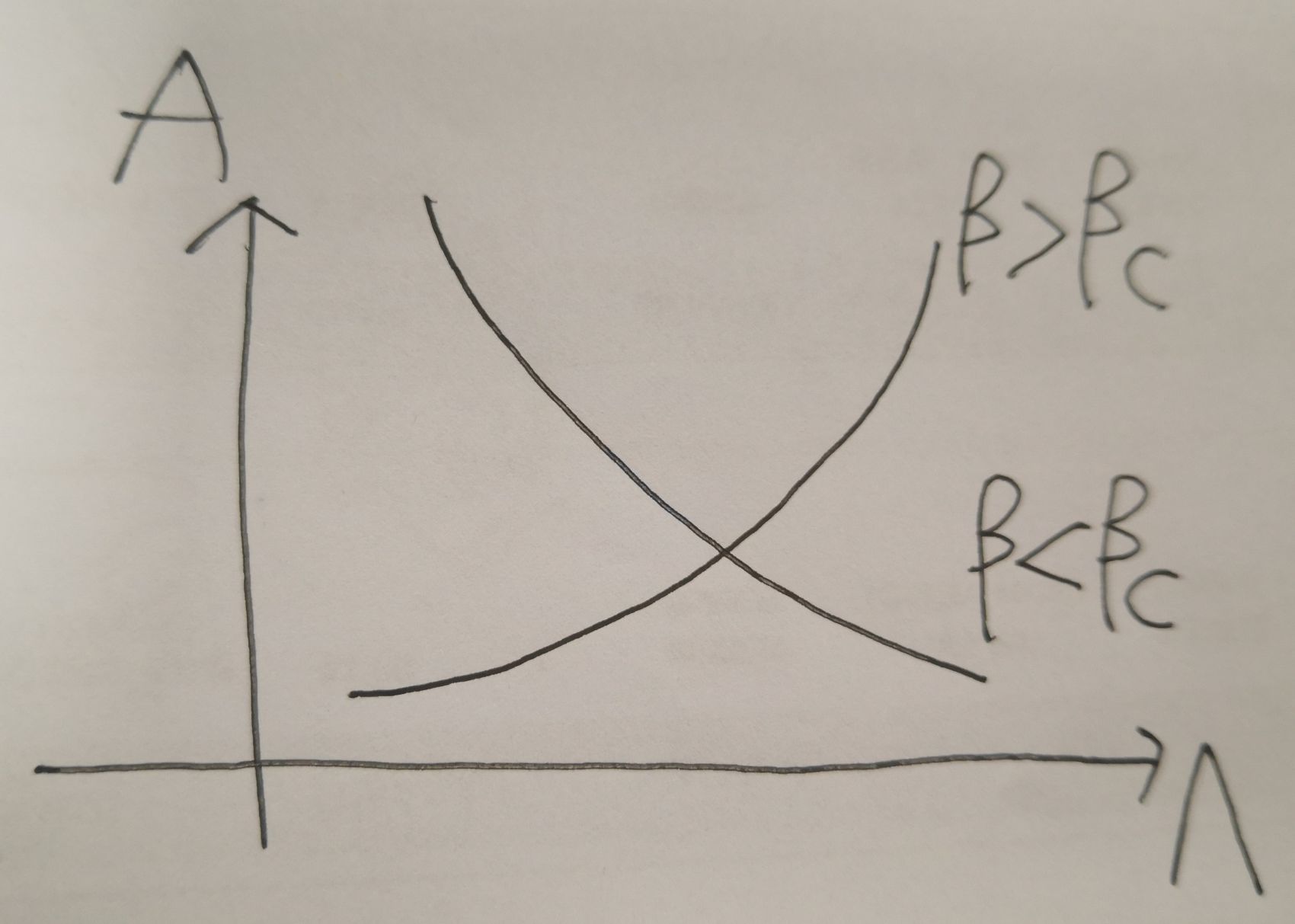
13. 文小刚书中文版3.3.12节中BKT相变的相图，文小刚书讨论的形式为\(S=\int d^2x[\frac{\eta_l}{2}(\partial_x\theta_l)^2-g_lcos\theta_l]\)，不考虑\(\eta_{\lambda}\)的重整化，相图为

    

    
    当考虑\(\eta_{\lambda}\)项重整化时，相图为

    

    
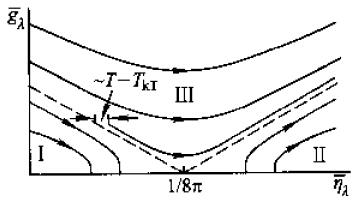
    相变点：图中均为\(\eta_{\lambda}=\frac{1}{8\pi}\)，对应于BKT相变的相变点\(k_BT=\frac{\pi}{2}Ja^2\)
14. 学生笔记
15. 学生笔记2
16. 学生笔记3

4.14 周四

1. 上节课龚老师总结
2. 本课程参考：
   1. Introduction to Bosonization,Miranda
   2. Shankar第17，18章
   3. 玻色化C.L.Kane Note
   4. 玻色化tokura Note
   5. 建议阅读Miranda Note的第3-16页，Tokura Note的1-6页，就能把这次课和下次课都弄懂
3. 附注一：相干态，可参考任意与量子光学相关的教材
   湮灭算符的本征态\(a|\psi\rangle=\alpha|\psi\rangle\rightarrow|\psi\rangle=e^{-|\alpha|^2/2}e^{\alpha a^{\dagger}}|0\rangle\)
   电磁场量子化(可参考高等量子力学)\(E\propto\sum (a_pe^{-i\omega t+i\vec{p}\cdot\vec{x}}+a_p^{\dagger}e^{i\omega t-i\vec{p}\cdot\vec{x}})\)，故相干态是经典电磁场的本征态
4. 附注二：正规排序，可参考任意与量子光学相关的教材
   \(:A:=A-\langle 0|A|0\rangle\)，其中\(|0\rangle\)为真空态。在电磁场中，\(|0\rangle\)为无光子的真空态。
   \(A=A(a_i,a_i^{\dagger})\)，在正规排序中我们只做排序，不计算对易子，将湮灭真空态的算符放右侧，将能作用在真空态的产生算符放左侧，即\(:a_1^{\dagger}a_2a_3^{\dagger}a_4:=a_1^{\dagger}a_3^{\dagger}a_2a_4\)，这样我们就能得到和上一条等价的定义
   对Luttinger液体而言，真空态为\(|0\rangle=(k\leq0)all-filled\)，真正的作用在真空态的湮灭算符为\(c_{k\leq0}^{\dagger},c_{k\geq0}\)，作用在真空态的产生算符为\(c_{k\leq0},c_{k\geq0}^{\dagger}\)
   对Luttinger液体的正规排序形式为\(:c_{k_1\geq0}c_{k_2\leq0}c_{k_3\geq0}^{\dagger}c_{k_4\leq0}^{\dagger}:=c_{k_2\leq0}c_{k_3\geq0}^{\dagger}c_{k_1\geq0}c_{k_4\leq0}^{\dagger}\)
   对\(:e^{i\Phi}:\)正规排序形式，\(\Phi=\Phi_++\Phi_-\)，其中\(\Phi_+\)全为产生算符，\(\Phi_-\)全为湮灭算符，则\(:e^{i\Phi}:=e^{i\Phi_+}e^{i\Phi_-}\)
5. 附注三：\(e^Ae^Be^{-[A,B]/2}=e^{A+B},e^Ae^B=e^{A+B}e^{[A,B]/2}\)，其中得满足\([A,[A,B]]=[B,[A,B]]=0\)，直接泰勒展开即可证明
6. 以下模型讨论的整个希尔伯特空间为\(H=\oplus_{n=-\infty}^{+\infty}H_n\)，n为\(k_F\)附近n个粒子的激发态或-n个粒子的湮灭态，F为Klein算子，F将\(H_n\)变为\(H_{n-1}\)，\(F^{\dagger}\)将\(H_n\)变为\(H_{n+1}\)
7. 上最终结论：\(\psi_i\sim e^{i\Phi_i},\Phi_i=\pi\int_{-\infty}^x\rho(x')dx'+\theta_i\)，其中\(\pi\int_{-\infty}^x\rho(x')dx'\)改变统计性质，\(\theta_i\)为相位涨落
   \(\psi=\frac{Fe^{i\Phi}}{\sqrt{2\pi a}}\)，\(a\rightarrow0^+\)为截断。其中i表示有多个独立的场，在Luttinger液体中\(i=L,R\)两种类型的场相互独立
   最终结论：\([\Phi_i(x),\Phi_i(y)]=i\pi H(x-y)\)，原因后续慢慢叙述，\(F_iF_j=-F_jF_i,F_i^2=1\)原因也后续叙述
8. 总之，Bosonization目的为：凑出\(\psi=\frac{Fe^{i\Phi}}{\sqrt{2\pi a}}\)中反对易关系，以及做实验只能观测到的关联函数等价、不同场\(\Phi_i\)不同让\(\psi_i\)无关联
9. 开始慢慢叙述：参考Miranda Note的第3-16页，Tokura Note的1-6页
   定义下列本征态形式如下：

   

   
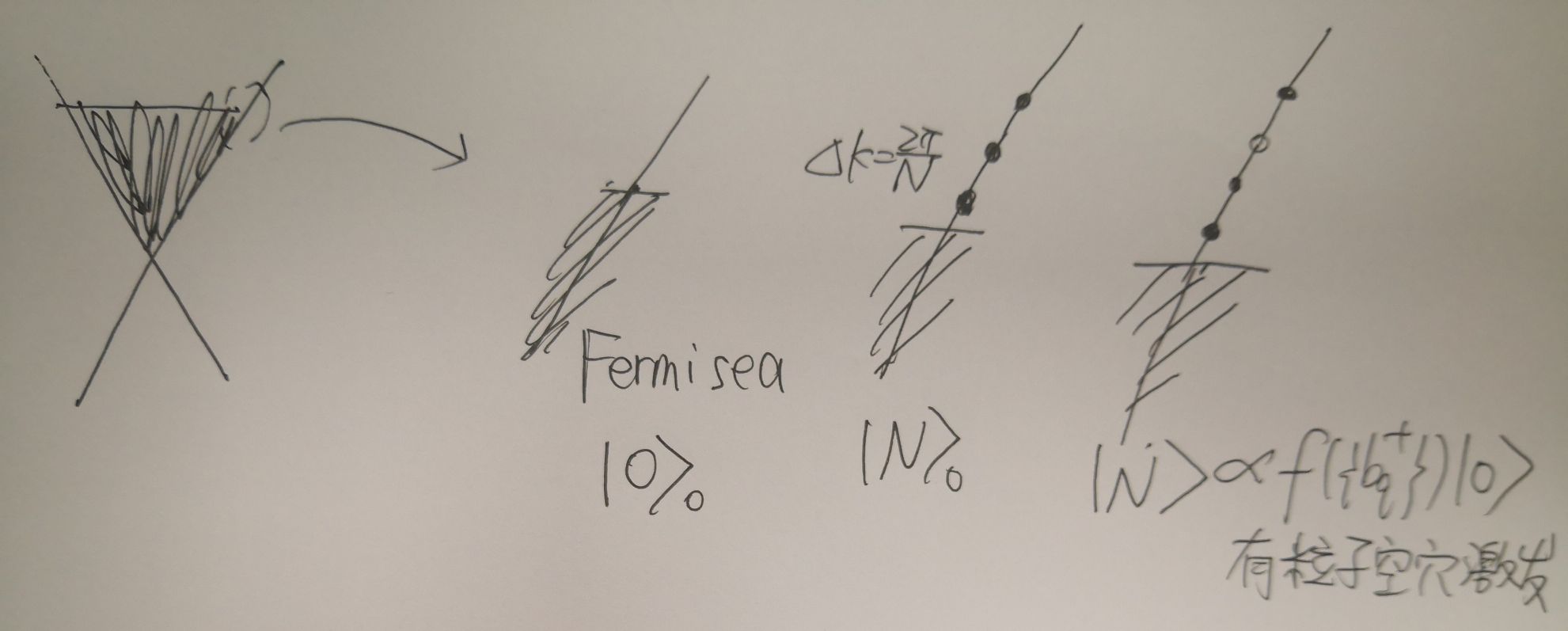
   一个很重要的引理：\(b_q|N\rangle_0=0\)，即\(|N\rangle_0\)为\(b_q\)的基态(\(b_q\)定义见Tokura Note的Eq17)，可以理解为没有粒子空穴对可以湮灭
   我们接下来要表示费米场\(\psi(x)=\frac{1}{\sqrt{L}}\sum_{k=-\infty}^{\infty}e^{-ikx}c_k\)
   总的希尔伯特空间形式\(H=\oplus_{n=-\infty}^{\infty}H_n\)，有粒子空穴激发的态写作\(|N\rangle_f=F^{\dagger}f\{b_q^{\dagger}\}|N\rangle_0\)，其中\(b_q,b_q^{\dagger}\)为玻色化后算符，具体可见Tokura Note的Eq17
   Klein算符F要保证费米子反对易，我们后续证明是反对易关系。F作用后形式为
   \(F^{\dagger}|N\rangle_f=F^{\dagger}f(\{b_q^{\dagger})\}|0\rangle_0=f(\{b_q^{\dagger}\})c_{k_0,N+1}^{\dagger}|N\rangle_0=f(\{b_q^{\dagger}\})|N+1\rangle_0\)
   同理，\(F|N\rangle_f=f(\{b_q^{\dagger}\})|N-1\rangle_0,F^{\dagger}F|N\rangle_f=|N\rangle_f,FF^{\dagger}|N\rangle_f=|N\rangle_f\)
10. 部分对易关系：
    \(\rho(x)=:\psi^{\dagger}(x)\psi(x):\),根据\([c_i^{\dagger}c_i,c_i]=-c_i\)可得\([\rho(x),\psi(y)]=-\psi(y)\delta(x-y)\)，由此可得\([\rho_q,\psi(y)]=-e^{-iq\cdot y}\psi(y)\)
    \([\rho(x),\psi(y)]=-\psi(x)\delta(x-y),[\rho_q,\psi(x)]=-e^{-iqx}\psi(x),[b_q,\psi(x)]=-\sqrt{\frac{2\pi}{L|q|}}e^{-iqx}\psi(x)=-\alpha_q(x)\psi(x)\)，其中\(\alpha_q=\frac{i}{\sqrt{n_q}}e^{iqx}\)
11. 证明\(\psi(x)|N\rangle_0\)为相干态：
    Tokura Note的Eq47证明了\([b_q^{\dagger},\psi(x)]=\alpha_q^*(x)\psi(x)\)，其中\(\alpha_q(x)=\frac{i}{\sqrt{n_q}}e^{iq\cdot x}\)
    故\(b_q\psi(x)|N\rangle_0=[b_q,\psi(x)]|N\rangle_0=\alpha_q(x)\psi(x)|N\rangle_0\)
    根据之前提到的对相干态的定义，有\(|\alpha_N(x)\rangle\equiv\psi(x)=\lambda e^{\sum_{q>0}\alpha_q(x)b_q^{\dagger}}|N-1\rangle_0\)
    Introducing Klein factor F，有
    \(\psi|N\rangle_0=F\lambda(x)e^{\sum_{q>0}\alpha_q(x)b_q^{\dagger}}|N\rangle_0=F\lambda(x)e^{-i\varphi^{\dagger}(x)}|N\rangle_0\)
    \( _0\langle N|F^{\dagger}\psi(x)|N\rangle_0=_0\langle N|F^{\dagger}F\lambda(x)e^{-i\varphi^{\dagger}(x)}|N\rangle_0=_0\langle N|e^{-i\varphi^{\dagger}(x)}\lambda(x)|N\rangle_0=\lambda(x)\)，由于之前提到的引理\(b_q|N\rangle_0=0\)，故\(_0\langle N|\varphi^{\dagger}(x)=0\)，因此\(\lambda(x)=\frac{1}{\sqrt{L}}e^{-ik_{0N}x}\)
12. 学生笔记
    学生笔记2
    学生笔记3