返回上级菜单
5.9 周一
- 参考:calculation of partition function,hubbard(1959)
参考:The Thouless-Andersn-Palmer equation in spin glass theory(数学家对着问题也感兴趣)
- Spin Glass技巧:Replica Trick,Replica Symmetry breaking,\(\cdot\cdot\cdot\)
还有一点比较重要的就是中心极限定理和大数定理,若\(X\sim N(\mu,\sigma^2)\),则\(\frac{X_1+X_2+\cdot\cdot\cdot+X_N}{N}\sim N(\mu,\frac{\sigma^2}{N})\),当统计数据足够多时,系统越来越接近于平均值
最常见的是在热学中应用,当统计\(10^{23}\)级别粒子平均值时,对经典粒子而言,围绕在平均值附近涨落可忽略不计;对费米子玻色子可严格按统计力学配分函数方法求涨落
- \(H=-\frac{J}{2N}\sum_{i\neq j}\sigma_i\sigma_j-h\sum_i\sigma_i\),其中\(\sum_{i\neq j}\)放弃了距离概念,是严格可解模型,2种解法,各有启发性。要抓住本质为相变
求解方式一
\(Z=Tr e^{\frac{\beta J}{2N}\sum_{i\neq j}\sigma_i\sigma_j+\beta h\sum_i\sigma_i}=Tr e^{\frac{\beta J}{2N}[(\sum_i\sigma_i)^2-N]+\beta h\sum_i\sigma_i}=e^{-\frac{\beta J}{2}}Tr[e^{\frac{\beta J}{2N}m^2+\beta hm}]\),其中\(m=\sum_i\sigma_i,\sigma_i=\pm1\)
\(\langle m\rangle=0,\langle m^2\rangle=\sum_{ij}\langle \sigma_i\sigma_j\rangle=\sum_i\langle\sigma_i^2\rangle=N\)
故原式\(=e^{-\beta J/2}\int P(m)e^{\frac{\beta J}{2N}m^2+\beta hm}dm\)
我们假设m满足高斯分布,满足之前提到的\(\langle m\rangle=0,\langle m^2\rangle=N\),可求出概率分布为\(P(m)=e^{-\frac{m^2}{2N}}\)
故原式\(=e^{-\beta J/2}\int e^{-\frac{m^2}{2N}+\frac{\beta J}{2N}m^2+\beta hm}dm=e^{-\beta F}\)
可求出相变点为\(\beta_cJ=1\),当\(\beta J<1\)时,积分结果收敛;当\(\beta J>1\),积分结果发散
可求出相变点附近磁化强度和磁化率\(m=\frac{\partial F}{\partial h},\chi=\frac{\partial m}{\partial h}\sim\frac{1}{T-J}\),和实验结果一致
求解方式二,参考
calculation of partition function,hubbard(1959)
利用公式\(\sqrt{\frac{A}{\pi}}\int e^{-Ax^2}dx=1,\sqrt{\frac{A}{\pi}}\int e^{-Ax^2+BAx}dx=e^{AB^2/4}\)
\(Z=e^{-\frac{\beta J}{2}}Tr e^{\frac{\beta J}{2N}m^2+\beta hm}=e^{-\frac{\beta J}{2}}Tr[\sqrt{\frac{2\beta J}{\pi N}}\int dqe^{-\frac{2\beta J}{N}q^2+m\frac{2\beta J}{N}q+\beta hm}]\)
我们认为Tr和\(\int\)可交换,故原式=\(e^{-\frac{\beta J}{2}}\sqrt{\frac{2\beta J}{\pi N}}\int dqe^{-\frac{2\beta J}{N}q^2}Tr[e^{\beta hm+\frac{2\beta Jq}{N}m}]\)
利用\(Tr(e^{B\sigma})=e^B+e^{-B}=2coshB\),故原式=\(e^{-\frac{\beta J}{2}}\sqrt{\frac{2\beta J}{\pi N}}\int dqe^{-\frac{2\beta J}{N}q^2+Nln[2cosh(\beta h+\frac{2\beta Jq}{N})]}=\int dqe^{-\beta f(q)}\)
其中f(q)图像如下图所示
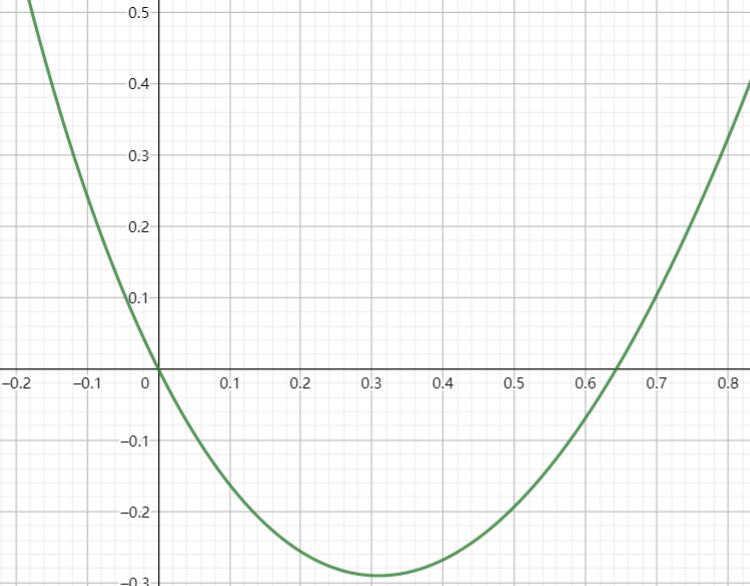
一般只考虑低温情形\(\beta\rightarrow+\infty\),\(f(q)=f(q_0)+\frac{1}{2}f''(q_0)(q-q_0)^2\),上式可用Mathematica求解
作业7:比较上述两种方法,龚老师上课没有讨论h的额外影响,请大家自己讨论h会造成的影响。本题为不确定题,没有标准答案,请大家自由发挥
- Spin Glass:\(H=-\sum_{ij}\frac{1}{2}J_{ij}\sigma_i\sigma_j\)
求解方式一
上一节课论述了\(Z=Tr[e^{-\beta H}]=e^{-\beta F}\),\(\beta\bar{F}=-\lim_{n\rightarrow0}\frac{\bar{z^n}-1}{n}\),\(\bar{z^n}=\int Tr[e^{-\beta\sum_{\alpha=1}^nH_{\alpha}}]P(J_{ij})DJ\)
假设\(\int Tr=Tr\int\)可交换,上节课论述了\(\bar{z^n}=exp[\frac{\beta^2J^2}{2}\sum_{\alpha\neq\beta}(\sum_i\sigma_i^{\alpha}\sigma_i^{\beta})^2]\)
定义\(\sum_i\sigma_i^{\alpha}\sigma_i^{\beta}=m_{\alpha\beta}\)。我们认为其仍然满足Gauss分布\(\langle m^{\alpha\beta}\rangle=0,\langle(m^{\alpha\beta})^2\rangle=N\),构造Gauss分布\(P(m^{\alpha\beta})=\sqrt{\frac{1}{2\pi N}}e^{-\frac{(m^{\alpha\beta})^2}{2N}}\)
\(\bar{Z^n}=Tr[e^{\frac{\beta^2J^2}{2}\sum_{\alpha\neq\beta}(m^{\alpha\beta})^2}]=\prod_{\alpha\neq\beta}Tr[e^{\frac{\beta^2J^2}{2}(m^{\alpha\beta})^2}]=\prod_{\alpha\neq\beta}\int P(m^{\alpha\beta})e^{\frac{\beta^2J^2}{2}(m^{\alpha\beta})^2}\)
相变点\(\frac{\beta_c^2J^2}{2}=\frac{1}{2N}\),当\(\beta<\beta_c\)时积分收敛,当\(\beta>\beta_c\)时积分发散
求解方式二,参考
calculation of partition function,hubbard(1959)
\(Tr[e^{\frac{\beta^2J^2}{2}(m^{\alpha\beta})^2}]=\sqrt{\frac{X}{\pi}}\int dq^{\alpha\beta}e^{-X(q^{\alpha\beta})^2+Yq^{\alpha\beta}m^{\alpha\beta}}\),其中\(\frac{Y^2}{4X}=\frac{\beta^2J^2}{2}\)
\(\bar{Z^n}=\int Dq^{\alpha\beta}(\sqrt{\frac{X}{\pi}})^ne^{-X\sum_{\alpha\neq\beta}(q^{\alpha\beta})^2}Tr[e^{\sum_{\alpha\neq\beta}Yq^{\alpha\beta}m^{\alpha\beta}}]\)
可以按照类似的办法接着往下计算
求解方式三,回到edwards-anderson model原始文献
原始文献第一句话:a dilute solution of say Mn in Cu can be modelled by an array of spins on the Mn arranged at random in the matrix of Cu
改进\(J_{ij}\sigma_i\sigma_j=\sum_i\sigma_i\xi_i\),\(\xi_i=\sum_jJ_{ij}\sigma_j\),表示每个自旋都能感受到势\(\xi_i\),有一定的独立性
剩余部分写入下一节课课程讲义
学生笔记
学生笔记2
学生笔记3
5.12 周四(为汶川大地震遇难同胞默哀)
- 佩服Anderson的直觉能力:他可以在非常复杂的问题中抽出简单的本质,而且敢于反对权威,打破固有陈旧概念的束缚。他的很多灵感完全来自于实验结果,许多人往往看到实验结果是按照现有理论凑出参数拟合实验结果,这种结果往往是大家能看到的
容易发好文章,但是换一个体系换一个实验不一定成立。一般这种敢于打破权威的工作不一定能发在好的杂志中,但它是更接近物理本质的工作。你若是认为势能是随机势,肯定会遭到周围许多人的反对,但Anderson敢这么做,见到了物理本质,也拿了诺奖
- 接续上一节课后半段,参考:edwards-anderson model原始文献
对于自旋构型为\(s=\{s_i\}\),其出现几率为\(\frac{e^{-\beta\sum_{i\neq j}J_{ij}s_is_j}}{Tr[e^{-\beta H}]}\),其中\(s_i=\pm1\),Tr表示对所有可能的态求和。故自旋构型为s的概率为
\(P(s)=e^{\beta F-\beta\sum_{ij}J_{ij}s_is_j}\),\(\sum_sP(s)=1\)
现在我们讨论的问题是初始时刻构型和末态构型之间的关联,定义\(s_i^{(1)}\)为\(t=0\)时刻的自旋,\(s_i^{(2)}\)为\(t=\infty\)时刻的自旋构型,求两个时刻的关联函数
\(P(s_i^{(1)},s_i^{(2)})=e^{2F-\sum_{ij}J_{ij}s_i^{(1)}s_j^{(1)}-\sum_{ij}J_{ij}s_i^{(2)}s_j^{(2)}}=e^{2F-\sum_i(\bar{s_i^{(1)}\xi_i^{(1)}+s_i^{(2)}\xi_i^{(2)}})}\)
额外补充:Quenched Disorder无序不随时间变化,Annealed Disorder无序随时间变化
继续求解P:若假设\(\xi_i\)是完全随机的
\(\langle\xi_i\rangle=0,\langle\xi_i^{(1)}\xi_i^{(1)}\rangle=\langle J_{ij}s_j^{(1)}J_{ik}s_k^{(1)}\rangle=\sum_jJ_{ij}^2\equiv J_0^2\),这里\(\equiv\)表示定义为
\(\langle\xi_i^{(1)}\xi_j^{(1)}\rangle=\langle\sum_{\alpha,\beta}J_{i\alpha}s_{\alpha}^{(1)}J_{j\beta}s_{\beta}^{(1)}\rangle=\sum_{\alpha}J_{i\alpha}J_{j\alpha}=0\)
\(P(s^{(1)},s^{(2)})=e^{2F-\sum_i(s_i^{(1)}\xi_i^{(1)}+s_i^{(2)}\xi_i^{(2)})}\),其中s和\(\xi\)是随机数,完全解耦
若假设\(\xi_i\)是非完全随机的,\(\langle s_i^{(1)}s_i^{(2)}\rangle=q\)
则\(\langle\xi_i^{(1)}\xi_i^{(2)}\rangle=\langle J_{ij}s_j^{(1)}J_{ik}s_k^{(2)}\rangle=\langle J_{ij}^2s_j^{(1)}s_j^{(2)}\rangle=qJ_0^2\neq0\)
则概率分布\(P(s^{(1)},s^{(2)},\xi^{(1)},\xi^{(2)})=Ne^{-\beta(s_i^{(1)}\xi_i^{(1)}+s_i^{(2)}\xi_i^{(2)})}P(\xi_i^{(1)},\xi_i^{(2)})\)
假设\(P(\xi_j^{(1)},\xi_j^{(2)})\)满足Gauss分布。备注:a href="./ref/edwardsanderson.pdf" target="_blank">edwards-anderson model原始文献中有一堆小错误,但处理问题的方式还是值得学习的
备注:\(\int dxdye^{A(x^2+y^2)+(q_1x+q_2y)+\alpha xy}\neq e^{q_1^2/A+q_2^2/A+\frac{\alpha^2}{A}q_1q_2}\),需要用二次型\(-A(x^2+y^2)+\alpha xy=-(1+\frac{\alpha}{2A})(x-y)^2+(1-\frac{\alpha}{2A})(x+y)^2\)来解出正确解
可以构造\(P(\xi_i^{(1)},\xi_i^{(2)})=exp[-A(\xi_i^{(1)})^2+(\xi_i^{(2)})^2+B\xi_i^{(1)}\xi_i^{(2)}]\)满足\(\langle\xi_i^{(1)}\xi_i^{(2)}\rangle=qJ_0^2\neq0,\langle\xi_i^{(1)}\xi_i^{(1)}\rangle=J_0^2\)
\(q=\langle s_i^{(1)}s_i^{(2)}\rangle=\frac{\int_{-1}^1\mu e^{-\mu\rho q}d\mu}{\int_{-1}^1e^{-\mu\rho q}d\mu}=-coth(\rho q)+\frac{1}{\rho q}\)
- 介绍部分随机微分方程(SDE,stochastic differential equasion;Random Stochastic Number;Random Process)
\(m\ddot{x}=-\frac{1}{\mu}\dot{x}+f+\xi,f=-\triangledown U\)
若\(\frac{1}{\mu}\)很大这是overdamped过程,该极限下\(\frac{1}{\mu}\dot{x}=f+\xi\)
则有\(\dot{x}=\mu(f+\xi)\),对于多分量情形有\(\dot{x}_i=\mu_i(f_i+\xi_i)\)
假设变为连续场,则\(\phi(x,t)\)有随机性,故\(\frac{\partial\phi(x,t)}{\partial t}=\mu(x)(f(x)+\xi(x))\)
当然,还可以在量子场论\(\phi^4\)理论上加随机力,有\(\frac{\partial\phi(x,t)}{\partial t}\sim\frac{\partial^2\phi}{\partial x^2}+\phi+\phi^3+\xi\)
- 其他随机微分方程:
Edwards-Wilkieson方程:\(\frac{\partial\phi}{\partial t}=\nu\frac{\partial^2\phi}{\partial x^2}+\xi\),当\(\xi=0\)时为扩散方程,当\(\nu=0\)时为Brown Motion
Kardar-Parisi-Zhang Model:\(\frac{\partial\phi}{\partial t}=\nu\frac{\partial^2\phi}{\partial x^2}+\frac{\lambda}{2}(\frac{\partial\phi}{\partial x})^2+\xi\)
这很类似Kuramoto Model:\(\frac{\partial\theta_i}{\partial t}=\omega_i+\frac{K}{N}\sum_jsin(\theta_i-\theta_j)+\xi_i\)
Edward Model:实验-生长过程;标度行为\(W(t)\sim\frac{1}{L}\sum_x\langle(\phi-\bar{\phi})^2\rangle\sim t^{\beta}\)
对Edvard方程\(\frac{\partial\phi}{\partial t}=\nu\frac{\partial^2\phi}{\partial x^2}+\xi\),有\(\langle\xi(t)\rangle=0,\langle\xi(t)\xi(t')\rangle=D\delta(t-t')\)
做傅里叶变换\(\phi(x,t)=\frac{1}{V}\sum_k\phi(k,t)e^{ikx},\xi(x,t)=\frac{1}{V}\sum_k\xi(k,t)e^{ikx}\)后有\(\frac{\partial\phi(k,t)}{\partial t}=-\nu k^2\phi(k,t)+\xi(k,t)\)
这本身是非平衡的系统,在不知道温度情况下无法定义\(\bar{\phi}\),我们一般情况下是设置\(t\rightarrow+\infty\)达到粒子平衡态来求解温度,后续龚老师将证明\(\langle\phi_k\phi_{-k}\rangle\sim\frac{1}{A+Bk^2}\),正比于图
- 下列参考:Kardar场的统计力学 chap9:Dissipative Dynamics,Kardar B站授课视频-场的统计物理
中心极限定理类比布朗运动:\(Y=\frac{X_1+X_2+\cdot\cdot\cdot+X_N}{N}\),当\(X_i\sim N(\mu,\sigma^2)\),则\(Y\sim N(\mu,\frac{\sigma^2}{N}),\sum_iX_i\sim N(N\mu,N\sigma^2)\)
类比布朗运动\(\langle x^2\rangle=2Dt=N\sigma^2\)
讨论Model:\(\dot{x}=\mu f+\eta\),f是梯度力,\(\eta\)是随机力
当\(\mu=0\)时,\(x=x_0+\int_0^t\eta(t')dt'\),\(\bar{x}=x_0,\sigma^2=\bar{x^2}-x_0^2=\int_0^t dt_1dt_2\langle\eta(t_1)\eta(t_2)\rangle=2Dt\),其中\(\langle\eta(t_1)\eta(t_2)\rangle=2D\delta(t_1-t_2),\langle\eta(t)\rangle=0,D=k_BT\mu\)
从量纲上看,\([D]=[k_BT]\cdot[\mu]\)
另外有一种处理方式是随机力做一个Gauss分布\(P(\eta(t))\sim exp[-\int\frac{1}{4D}\eta^2(t)dt]\)
学生笔记
学生笔记2
学生笔记3

