4.7 周四

1. 上节课内容总结：
   能打开相互作用Gap的形式\(\int Vcos(2k_Fx)\psi^{\dagger}\psi=\frac{V}{2}(\psi_R^{\dagger}\psi_L+h.c.)\)
   对于Boson子体系可变换到\(\rho,\theta\)共轭表象，其中\(\psi=e^{i\theta}\sqrt{\rho},\psi^{\dagger}=\sqrt{\rho}e^{-i\theta}\),\([\psi,\psi^{\dagger}]=i\hbar\rightarrow[\rho(x),\theta(y)]=i\delta(x-y)\)
   jordan-wigner and bosonization中给出了费米子到自旋的变换，具体形式如下：
   \(a^{\dagger}=\sigma^+\bigotimes I\bigotimes I,b^{\dagger}=\sigma^z\bigotimes\sigma^+\bigotimes I,c^{\dagger}=\sigma^z\bigotimes\sigma^z\bigotimes\sigma^+\)
   满足\(\{a,a^{\dagger}\}=I,\{a,b\}=\{a,b^{\dagger}\}=\{a^{\dagger},b^{\dagger}\}=0\)
   Jordan-Wigner变换，建立自旋和费米子对应关系\(\sigma_i=exp[i\pi c_j^{\dagger}c_j]c_i\)
   连续化并变换成费米子形式\(\psi(x)=exp[i\pi\int_{-\infty}^x\rho(x')dx']e^{i\theta(x)}\sqrt{\rho(x)}\)
   上式为Lectures on bosonization,C.L.Kane中Eq37式，为费米子到玻色子的Jordan-Wigner变换
   C.L.Kane Note是通过格林函数的方法证明这个形式在真空态期望值下计算格林函数，直接用费米子方法算和玻色化后用玻色子方法算，效果等价(本课程不要求掌握)

   

   
   实际上我们只考虑费米面附近的微小涨落，故常常取\(\rho=n_0+\delta\rho\)，在shankar17-19章和Lectures on bosonization,C.L.Kane中忽略掉了\(\sqrt{\rho}\)项，并证明出对于宏大费米海中费米面附近微小激发是等价的
   故1D费米海情况下费米子到玻色子变换形式为\(\psi(x)=exp[i\pi\int_{-\infty}^x\rho(x')dx'+i\theta(x)]\)
2. 费米玻色对应\(Z_F=Z_B\)另一种推导如下所示：
   1D费米海边缘激发谱为\(\epsilon_k=v|k|,k=\frac{n\pi}{L}\)，故激发能量-动量是线性关系且是量子化的，故对Fermion而言，激发的空间为：
   \(|100000000\cdot\cdot\cdot\rangle,|010000000\cdot\cdot\cdot\rangle,|110000000\cdot\cdot\cdot\rangle,\cdot\cdot\cdot\)，其中\(|111000000\cdot\cdot\cdot\rangle,\cdot\cdot\cdot\)代表激发了3个费米子，能量为\(\frac{v\pi}{L},\frac{2v\pi}{L},\frac{3v\pi}{L}\)
   费米子配分函数为\(Z_F=(\prod_{n=1}^{+\infty}(1+e^{-\beta n\pi v/L}))^2=e^{-\beta F}\)，其中平方项来自于费米面左右两端\(-K_F,K_F\)附近的激发看成是赝自旋
   \(e^{-\beta F}=2\sum_{n=1}^{+\infty}ln(1+e^{-\beta\frac{\pi v}{L}n})\)，令\(a=\beta\frac{\pi v}{L}\langle\langle1\)，可连续化得\(-\beta F=2\int_0^{+\infty}ln(1+e^{-an})dn=\frac{\pi^2}{6a}\)
   利用级数展开求和公式\(\sum_{n=0}^{+\infty}\frac{(-1)^n}{(n+1)^2}=\frac{pi^2}{12}\)，得\(-\beta F=\frac{\pi^2}{6a}\)
   Boson Field，不考虑赝自旋，配分函数满足\(Z_B=\prod_{n=1}^{+\infty}\frac{1}{1-e^{-\beta v\pi n/L}}=e^{-\beta F}\)
   根据级数展开求和公式\(\sum_{n=0}^{+\infty}\frac{1}{(n+1)^2}=\frac{\pi^2}{6}\)，可得\(-\beta F=\frac{\pi^2}{6a}\)
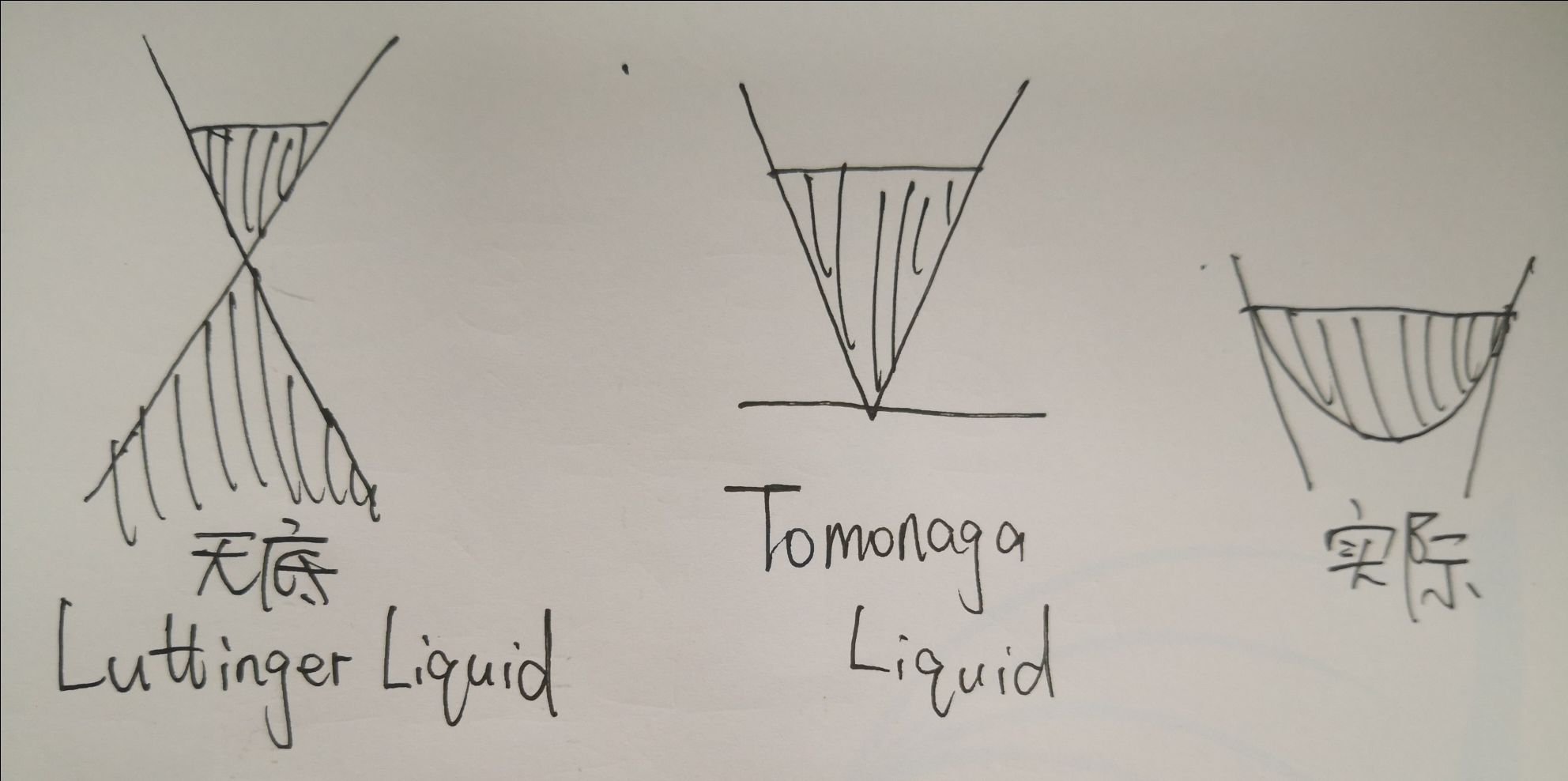
   于是费米玻色对偶得证，1933-1934Bloch证明出\(C_{vF}=C_{vB}\)，为Bloch声波理论，原始文献为德文
   Fermi-Bose对偶图片如下图所示：

   

3. 今日讲解内容：Luttinger-Tomonaga Model，参考：
   1. mahan书324-352页
   2. Lectures on bosonization,C.L.Kane
   3. tomonaga原始论文
   4. luttinger原始论文
   5. Fermions in one-dimension:Tomonaga-Luttinger Liquid,Sachdev
   6. shankar17-19章
   7. An introduction to bosonization,senechal
   8. Cazalilla,bosonization one-dimensional cold atom gases
   9. Introduction to one dimensional physics and luttinger liquid
   10. 诺贝尔奖Haldane,1979-1981年间论文，包括：
   11. 论文1
   12. 论文2
4. 推荐：tomonaga原始论文的Introduction部分
   出发点：3D情况下存在Fermi Liquid Theory，可用单电子近似\(m\rightarrow m^*\)，可较好采用平均场理论，各波独立无关联
   但是当1D情形下相互作用很强时微扰论要逐渐算到高阶项。这里我们改变方法，用Bloch提出的声波理论，不去处理一堆多体费米子系综，而是处理一个个单体玻色声子
5. 1D情况下Bose化情形，以下内容均可参考：Lectures on bosonization,C.L.Kane、Fermions in one-dimension:Tomonaga-Luttinger Liquid,Sachdev
   \(\rho(x)=\psi^{\dagger}(x)\psi(x),\psi(x)=\frac{1}{\sqrt{L}}\sum_ke^{ik\cdot x}c_k,\rho(x)=\frac{1}{\sqrt{L}}\sum_{kk'}e^{-ik\cdot x+ik'\cdot x}c_k^{\dagger}c_{k'}\)
   傅里叶变换：\(\rho(x)=\frac{1}{L}\sum_qe^{iq\cdot }\rho_q\)，为了凑出\(\rho_q\)具体值，我们将上式令\(k'=k+q\)，可得
   \(\rho_q=\sum_kc_k^{\dagger}c_{k+q}\)，相当于湮灭所有可能的\(k+q\)粒子并产生k粒子
   下一个问题：两个费米算符cc具有玻色算符性质，三个费米算符ccc具有费米算符性质。下面我们来考察以下\([\rho_q,\rho_{q'}]\)的性质：
   \([c_i^{\dagger}c_j,c_k^{\dagger}c_l]=c_i^{\dagger}c_jc_k^{\dagger}c_l-c_k^{\dagger}c_lc_i^{\dagger}c_j=c_i^{\dagger}(\delta_{jk}\pm c_k^{\dagger}c_j)c_l-c_k^{\dagger}(\delta_{li}\pm c_i^{\dagger}c_l)c_j=c_i^{\dagger}c_l\delta_{jk}-c_k^{\dagger}c_j\delta_{li}\)
   上式中\(\pm\)表示c为费米子或玻色子，我们看到由于消去关系，该结果对费米子和玻色子是一样的，从这个角度可以说明两个费米算符cc具有费米算符的性质
   \([\rho_q,\rho_{q'}]=\sum_{nn'}[c_n^{\dagger}c_{n+q},c_{n'}^{\dagger}c_{n'+q'}]=\sum_nc_n^{\dagger}c_{n'+q'}|_{n'=n+q}-c_{n'}^{\dagger}c_{n+q}|_{n=n'+q'}=\sum_n(c_n^{\dagger}c_{n+q+q'}-c_{n-q'}^{\dagger}c_{n+q})\)
   如果费米子在全空间内都可以填充，则上式为0，但事实显然于此违背。考虑Tomonaga Liquid和Luttinger Liquid

   

   
   求解对易关系\([\rho_q,\rho_{q'}]=\sum_n(c_n^{\dagger}c_{n+q+q'}-c_{n-q'}^{\dagger}c_{n+q})\)，具体图像如下所示，箭头起始端表示湮灭终点端表示产生

   

   
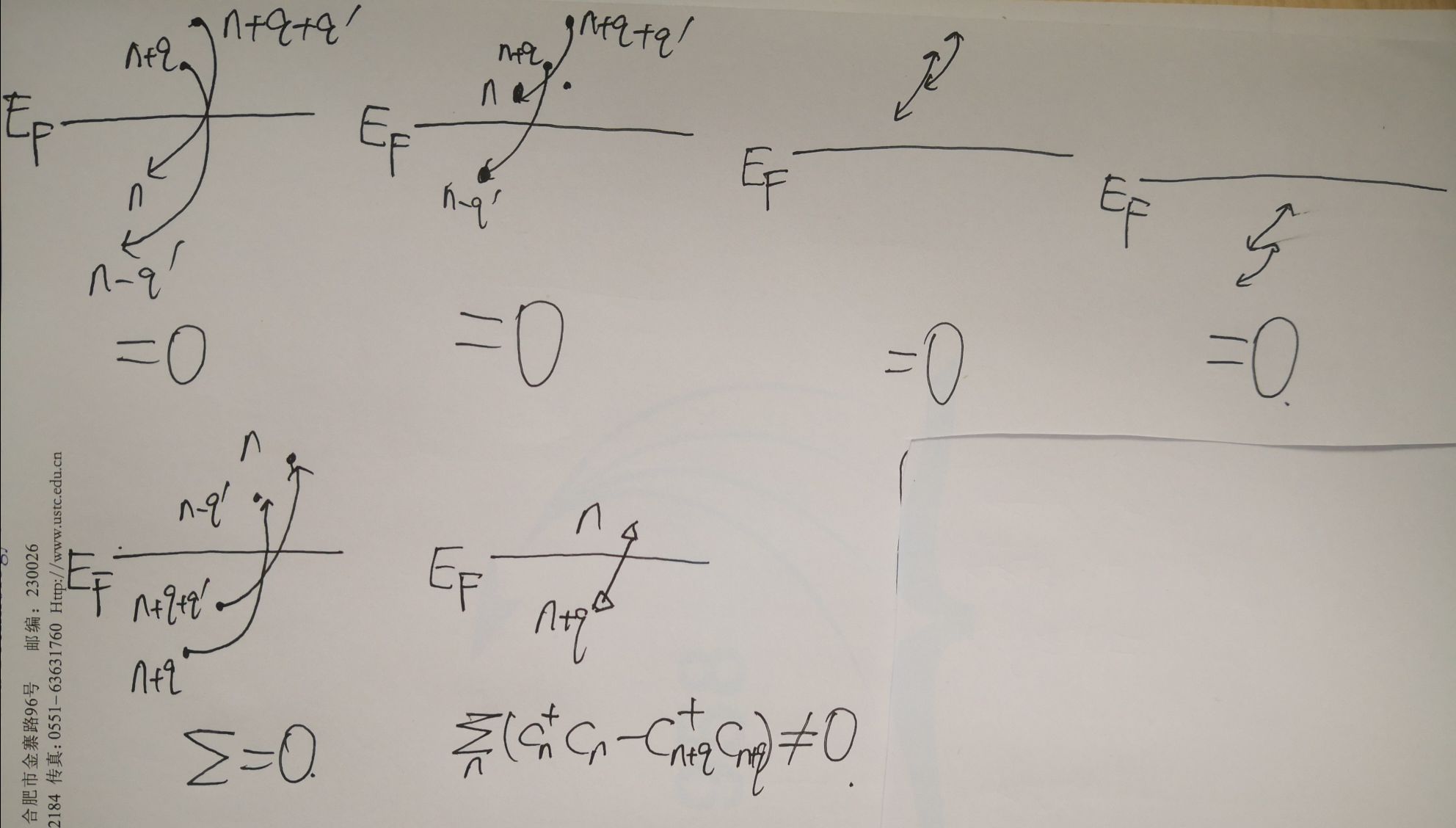
   据此可算出\([\rho_q,\rho_{q'}]=-q\frac{L}{2\pi}\delta_{q,-q'}\)
6. 建立\(\rho_q\)与\(b^{\dagger},b\)关系来完成玻色化
   我们作类比，\([\rho_q,\rho_{-q}]=-q\frac{L}{2\pi},[b,b^{\dagger}]=1\)，令\(\rho_q=\sqrt{-q\frac{L}{2\pi}}b,\rho_{-q}=\sqrt{-q\frac{L}{2\pi}}b^{\dagger}\)
   故k空间内的算符\(\rho_q=\sum_nc_n^{\dagger}c_{n+q}\)对于Fermion而言是将\(n+q\)处的费米子移动到n处，对于Boson子而言是产生或湮灭一个Boson子
   注：\(q=0\)为宏大背景态，需要扣除掉，故上面对易关系，\(\rho_q\sim b_q\)对偶关系只在\(q\neq0\)成立
7. 证明\(\rho_q=\sqrt{-q\frac{L}{2\pi}}b\)的等价性
   令\(H^F=v\sum_n\frac{n\pi}{L}c_n^{\dagger}c_n,H^B=\sum_{q>0}\frac{\pi}{L}v_Fqb_q^{\dagger}b_q\)，则有\([H^F,\rho_q]=[H^B,\rho_q]=-v_F\frac{\pi q}{L}\rho_q\)
   \([H^F,\rho_q]=v\sum_{nm}\frac{n\pi}{L}[c_n^{\dagger}c_n,c_m^{\dagger}c_{m+q}]=v\sum_{nm}\frac{n\pi}{L}(c_n^{\dagger}c_{m+q}|_{n=m}-c_m^{\dagger}c_n|_{m+q=n})=v\sum_n\frac{n\pi}{L}(c_n^{\dagger}c_{n+q}-c_{n-q}^{\dagger}c_n)=v\sum_n[\frac{n\pi}{L}-\frac{(n+q)\pi}{L}]c_n^{\dagger}c_{n+q}=-v\frac{\pi q}{L}\rho_q\)
   \(H_F,H_B\)对应的运动方程是一样的，\(i\dot{\rho}_q=[H_F,\rho_q],i\dot{\rho}_q=[H_B,\rho_q]\)
   shankar17-19章和Lectures on bosonization,C.L.Kane还额外论述了关联函数的等价性(不要求掌握)
8. 最后讲解历史：
   1933-1934,Bloch提出1D玻色子体系和费米子体系自由能F和热容\(c_v\)相等，原始文献为德文
   1950年，tomonaga原始论文。Tomonaga指出Interacting Fermion有Boson激发，缺点是用了许多Lots of Approximation
   1963年，luttinger原始论文
   Bohm在研究固体中等离激元振荡时也采用了类似Bloch的方法(tomonaga原始论文introduction部分中大致介绍了，其论文在当时unpublished)
   1975年，Spin Model和XXZ Model
   1980年，Haldane提出可以直接从\(L_F\)写出玻色场\(L_B[\phi]\)并构造\(\psi=e^{i\phi}\)(采用Jordan-Wigner变换)
   1984年，Witten提出非阿贝尔玻色化，witten原始论文
9. 学生笔记
10. 学生笔记2