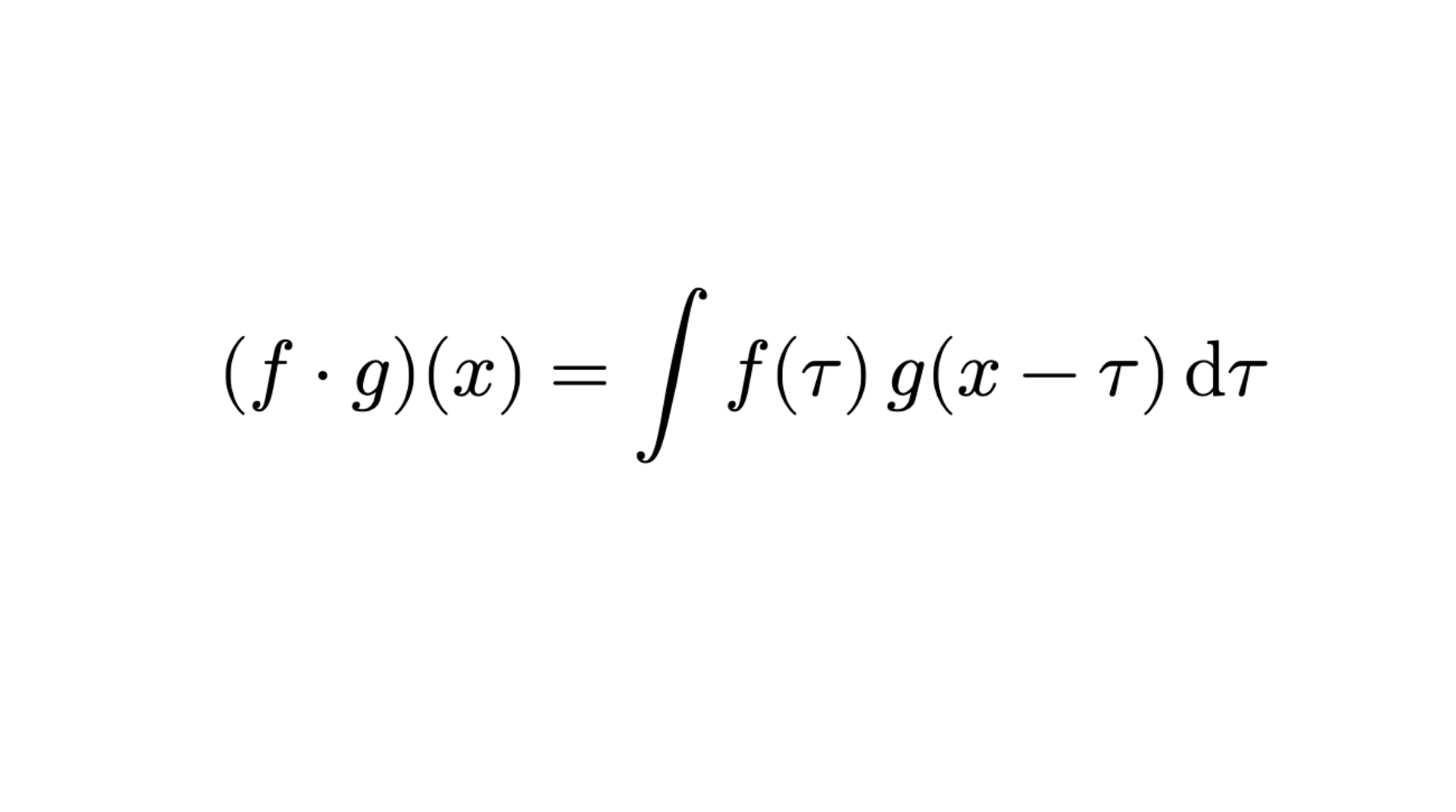符号计算改良的分析化学计算方法

View in PDF Attachments

摘要

  两性物质 NaHA\text{NaHA} 溶液的 PH\text{PH} 计算是分析化学的重要内容。教科书介绍了多种 PH\text{PH} 近似公式，但各公式的适用条件一度缺少详细论证，且目前仍然处于争论之中。本文以 Mathematica\text{Mathematica} 符号计算软件为辅助，发扬了分析化学去公式化计算方法。针对学术界一直头疼的NaHA\text{NaHA} 酸碱度计算公式的选择问题，作者利用数学分析方法及可视化手段，深刻揭示了各公式的可行域空间，力求为分析化学师生彻底扫除障碍。

引言

  二元弱酸 H2A\text{H}_2\text{A} 的酸式盐 NaHA\text{NaHA} 为两性物质。在浓度为 cc 的 NaHA\text{NaHA} 溶液中有以下关系：

  1. 电荷守恒： [Na+]+[H+]=[HA−]+2[A2−]+[OH−][Na^+]+[H^+]=[HA^-]+2[A^{2-}]+[OH^-]
  2. 物料守恒： [Na+]=[H2A]+[HA−]+[A2−][Na^+]=[H_2A]+[HA^-]+[A^{2-}]
  3. 一级电离： K1=[H+][HA−][H2A]K_1=\frac{[H^+][HA^-]} {[H_2A]}
  4. 二级电离： K2=[H+][A2−][HA−]K_2=\frac{[H^+][A^{2-}]} {[HA^-]}
    为了简化计算，引入分析浓度 cc（A的总浓度）与分布分数（组分占有 cc 的比例）：

[H2A]=c∗[H+]2[H+]2+[H+]K1+K1K2[HA−]=c∗[H+]K1[H+]2+[H+]K1+K1K2[A2−]=c∗K1K2[H+]2+[H+]K1+K1K2\begin{aligned} [H_2A]&=c*\frac{[H^+]^2}{[H^+]^2+[H^+]K_1+K_1K_2} \\ [HA^-]&=c*\frac{[H^+]K_1}{[H^+]^2+[H^+]K_1+K_1K_2} \\ [A^{2-}]&=c*\frac{K_1K_2}{[H^+]^2+[H^+]K_1+K_1K_2} \end{aligned}

将上述组分浓度代入电荷守恒，得到关于氢离子浓度[H+][H^+]的高次多项式方程：

c+[H+]=[H+]K1+2K1K2[H+]2+[H+]K1+K1K2+Kw[H+] c+[H^+]= \frac{[H^+]K_1+2K_1K_2}{[H^+]^2+[H^+]K_1+K_1K_2} +\frac{K_w}{[H^+]}

其中 KwK_w 为水的离子积常数，此处默认常温下 Kw=10−14K_w=10^{-14} 。对于给定的二元酸式盐 NaHA\text{NaHA} ，已知两级电离常数 K1K_1 和 K2K_2 ，给定浓度 cc ，求解上述方程即可得知此时氢离子浓度的准确值（忽略离子活度）。但由于上述方程求解不便，传统分析化学的处理方法为引入近似条件，将氢离子浓度[H+][H^+]化简为显函数形式。以下是经典教科书中给出的四个近似公式及其适用条件：

[Hx1]=K1(c∗K2+Kw)c+K1c≥500K2[Hx2]=K1(c∗K2)c+K1c≥500K2  &&  K2c≥20Kw[Hx3]=K1K2c≥20K1[Hx4]=K1(c∗K2+Kw)cc≥500K2  &&  K2c≥20Kw\begin{aligned} [H_{x1}]&= \sqrt{\frac{K_1(c *K_2+Kw)}{c+K_1}}&c&\geq500K_2\\ [H_{x2}]&= \sqrt{\frac{K_1(c *K_2)}{c+K_1}} &c&\geq500K_2 \;\&\&\;K_{2}c\geq20K_w \\ [H_{x3}]&= \sqrt{K_1K_2} &c&\geq20K_1\\ [H_{x4}]&= \sqrt{\frac{K_1(c *K_2+Kw)}{c}} &c&\geq500K_2\;\&\&\;K_{2}c\geq20K_w \end{aligned}

  传统体系“记忆换运算，近似换简化”的思路同学们都不陌生。然而，这样的近似公式会造成学习上的不便甚至混淆：

  1. 一些公式的适用范围存在交集，实际应用中究竟哪一个公式适用区间更普遍？
  2. 适用的边界条件究竟如何与 物理意义(二级电离、水的电离)相联系？

  在计算机高度发达的今天，我们可以很轻易地求解高次多项式方程，传统近似手段简化运算的价值正逐渐丧失。并且，如何真正完备地刻画使用公式带来的误差以及它们的适用范围，成为目前去公式化方法和传统体系之间的主要矛盾。为此，本文以 Mathematica\text{Mathematica} 为平台，充分运用数学、计算机手段，讨论近似公式的可行域区间，推动分析化学课程的发展。

数学准备

可行域

  由于 [H+][H^+]、K1K_1、K2K_2，cc 数值非常小，对它们取负对数之后， PHPH、PK1PK_1、PK2PK_2、PcPc 四个变量满足的关系如下：

PH1=−log⁡1010−PK1(10−Pc∗10−PK2+Kw)10−Pc+10−PK1PH2=−log⁡1010−PK1(10−Pc∗10−PK2)10−Pc+10−PK1PH3=−log⁡1010−PK1∗10−PK2PH4=−log⁡1010−PK1(c∗10−PK2+Kw)10−Pc\begin{aligned} PH_1&=-\log_{10} \sqrt{\frac{10^{-PK_1}(10^{-Pc} *10^{-PK_2}+Kw)}{10^{-Pc}+10^{-PK_1}} }\\ PH_2&= -\log_{10} \sqrt{\frac{10^{-PK_1}(10^{-Pc} *10^{-PK_2})}{10^{-Pc}+10^{-PK_1}}}\\ PH_3&=-\log_{10} \sqrt{10^{-PK_1}*10^{-PK_2}}\\ PH_4&=-\log_{10} \sqrt{\frac{10^{-PK_1}(c *10^{-PK_2}+Kw)}{10^{-Pc}}} \end{aligned}

引入相空间 R3={  x=(PK1,PK2,Pc)  ∣  PK1,PK2,Pc∈R  }\mathbb{R}^3=\{\;\bm{x}= (PK_1,PK_2,Pc)\;|\;PK_1,PK_2,Pc\in \mathbb{R}\;\} 以描述已知的三个初始条件。如此一来，四大公式可看作 R3→R,(x  →  PH)\mathbb{R}^3\rightarrow \mathbb{R},(\bm{x}\;\rightarrow \;PH) 一个映射。

  我们的目的，在于找出所有满足“相对准确值误差在5%5\%以内”的三维点所构成的集合。由函数的连续性可知，它是一个连通集。以相对氢离子准确值误差 5%5\%为标准，设 PHPH 准确值为 F(x),x=(PK1,PK2,Pc)F(\bm{x}),\bm{x} = (PK_1,PK_2,Pc) ，定义误差函数 Δ(x),x∈R3\Delta (\bm{x}),\bm{x}\in \R^3。简单推导可知，Δ(x)=∣  fi(x)−F(x)  ∣≤0.02\Delta(\bm{x})=|\;f_i(\bm{x})-F(\bm{x})\;|\leq0.02即为所求区域满足的限制条件。我们称不等式的解集为可行域。

对数变换

  将这一对应关系写作：

f1(PK1,PK2,Pc)=−log⁡1010−PK1(10−Pc∗10−PK2+Kw)10−Pc+10−PK1f2(PK1,PK2,Pc)=−log⁡1010−PK1(10−Pc∗10−PK2)10−Pc+10−PK1f3(PK1,PK2,Pc)=−log⁡1010−PK1∗10−PK2f4(PK1,PK2,Pc)=−log⁡1010−PK1(10−Pc∗10−PK2+Kw)10−Pc\begin{align*} f_1(PK_1, PK_2, Pc)&=-\log_{10} \sqrt{ \frac{10^{-PK_1}(10^{-Pc} *10^{-PK_2}+Kw)}{10^{-Pc}+10^{-PK_1}} } \\ f_2(PK_1, PK_2, Pc)&= -\log_{10} \sqrt{ \frac{10^{-PK_1}(10^{-Pc} *10^{-PK_2})}{10^{-Pc}+10^{-PK_1}} } \\ f_3(PK_1,PK_2,Pc)&=-\log_{10} \sqrt{ 10^{-PK_1}*10^{-PK_2} }\\ f_4(PK_1,PK_2,Pc)&=-\log_{10} \sqrt{ \frac{10^{-PK_1}(10^{-Pc} *10^{-PK_2}+Kw)}{10^{-Pc}} }\\ \end{align*}

由数学分析知识可知，所有满足条件的点，在相空间中分布于边界曲面的同一侧。对原方程作对数变换：

10−Pc+10−PH=10−PH10−PK1+2∗10−PK110−PK210−2PH+10−PH10−PK1+10−PK110−PK2+Kw10−PH 10^{-Pc}+10^{-PH}= \frac{10^{-PH}10^{-PK_1}+2*10^{-PK_1}10^{-PK_2}} {10^{-2PH}+10^{-PH}10^{-PK_1}+10^{-PK_1}10^{-PK_2}} +\frac{K_w}{10^{-PH}}

几乎无法表示为PHPH关于PK1PK_1、PH2PH_2、PcPc 的显函数，误差函数 Δ(x)\Delta (\bm{x}) 难于推导。故退而寻求数值解。

线性近似公式的解析与讨论

作图

  公式 [Hx3][H_{x3}] 经对数变换后的形式较为简单——$PH $关于 PK1PK_1 和 PK2PK_2具有线性性质，在新的相空间 R3={  y=(PK1,PK2,PH)  ∣  PK1,PK2,PH∈R  }\R^3=\{\;\bm{y}= (PK_1,PK_2,PH)\;|\;PK_1,PK_2,PH\in R\;\}中的图像是一张平面：

PH=12PK1+12PK2 PH=\frac{1}{2}PK_1+\frac{1}{2}PK_2

  在相空间 R3={  y=(PK1,PK2,PH)  ∣  PK1,PK2,PH∈R  }\R^3=\{\;\bm{y}= (PK_1,PK_2,PH)\;|\;PK_1,PK_2,PH\in R\;\}中，满足与精确酸度方程误差0.020.02 的两张曲面分别是：

10−Pc+10−(PH−0.02)=10−(PH−0.02)10−PK1+2∗10−PK110−PK210−2(PH−0.02)+10−(PH−0.02)10−PK1+10−PK110−PK2+Kw10−(PH−0.02)10−Pc+10−(PH+0.02)=10−(PH+0.02)10−PK1+2∗10−PK110−PK210−2(PH+0.02)+10−(PH+0.02)10−PK1+10−PK110−PK2+Kw10−(PH+0.02)\begin{aligned} 10^{-Pc}+10^{-(PH-0.02)}&= \frac{10^{-(PH-0.02)}10^{-PK_1}+2*10^{-PK_1}10^{-PK_2}} {10^{-2(PH-0.02)}+10^{-(PH-0.02)}10^{-PK_1}+10^{-PK_1}10^{-PK_2}} +\frac{K_w}{10^{-(PH-0.02)}}\\ 10^{-Pc}+10^{-(PH+0.02)}&= \frac{10^{-(PH+0.02)}10^{-PK_1}+2*10^{-PK_1}10^{-PK_2}} {10^{-2(PH+0.02)}+10^{-(PH+0.02)}10^{-PK_1}+10^{-PK_1}10^{-PK_2}} +\frac{K_w}{10^{-(PH+0.02)}} \end{aligned}

与PH=12PK1+12PK2PH=\frac{1}{2}PK_1+\frac{1}{2}PK_2联立消去 PHPH，即得 R3\mathbb{R}^3中关于 (PK1,PK2,Pc)(PK_1,PK_2,Pc)的方程

10−Pc+10−(12PK1+12PK2−0.02)=10−(12PK1+12PK2−0.02)10−PK1+2∗10−PK110−PK210−2(12PK1+12PK2−0.02)+10−(12PK1+12PK2−0.02)10−PK1+10−PK110−PK2+Kw10−(12PK1+12PK2−0.02)10−Pc+10−(12PK1+12PK2+0.02)=10−(12PK1+12PK2+0.02)10−PK1+2∗10−PK110−PK210−2(12PK1+12PK2+0.02)+10−(12PK1+12PK2+0.02)10−PK1+10−PK110−PK2+Kw10−(12PK1+12PK2+0.02)\begin{aligned} 10^{-Pc}+10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 -0.02)}&= \frac{10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 -0.02)}10^{-PK_1}+2*10^{-PK_1}10^{-PK_2}} {10^{-2(\frac{1}{2}PK_1+\frac{1}{2}PK_2 -0.02)}+10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 -0.02)}10^{-PK_1}+10^{-PK_1}10^{-PK_2}} \\ &+ \frac{K_w}{10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 -0.02)}} \\ 10^{-Pc}+10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 +0.02)}&= \frac{10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 +0.02)}10^{-PK_1}+2*10^{-PK_1}10^{-PK_2}} {10^{-2(\frac{1}{2}PK_1+\frac{1}{2}PK_2 +0.02)}+10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 +0.02)}10^{-PK_1}+10^{-PK_1}10^{-PK_2}} \\ &+\frac{K_w}{10^{-(\frac{1}{2}PK_1+\frac{1}{2}PK_2 +0.02)}} \end{aligned}

对应的曲面即是可行域的边界。分别记作 sup (x)\text{sup}\,(\bm{x}) 和 inf (x)\text{inf}\,(\bm{x})，作图如下：

完整可行域

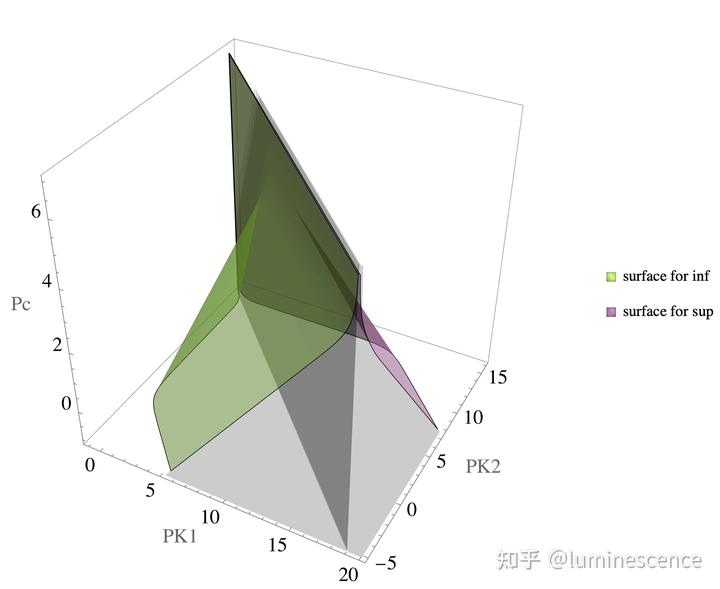
可行域就是图中的阴影区域。

讨论

  公式 f3f_3 的秘密已经一览无余。比如固定 Pc=2Pc=2，误差函数

Δ(PK1,PK2,2)=∣  f3(PK1,PK2,2)−F(PK1,PK2,2)  ∣ \Delta (PK_1,PK_2,2)=|\; f_3(PK_1,PK_2,2)-F(PK_1,PK_2,2)\;|

的解为 R2\mathbb{R}^2 的子集，是可行域在 Pc=2Pc=2 处的截面：

截面

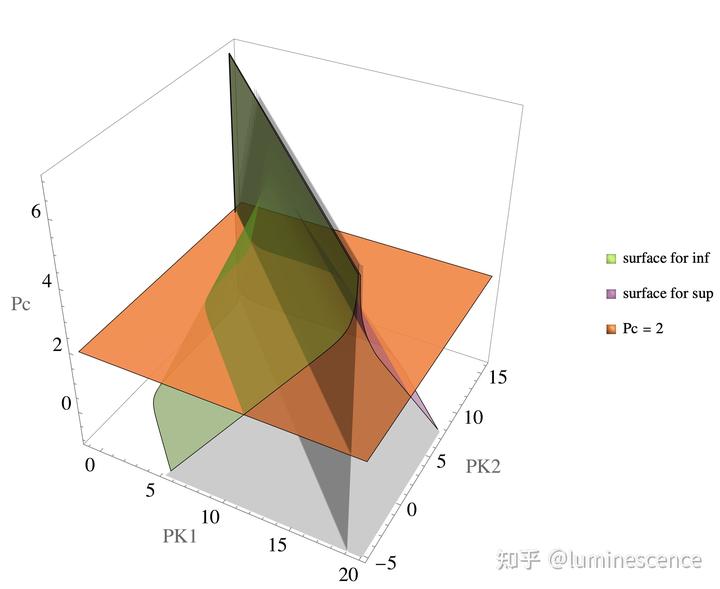
  又如，对公式的适用条件

c≥500K2          condition  1c≥500K2  &&  K2c≥20Kwcondition  2c≥20K1condition  3\begin{aligned} &c\geq500K_2\;\;\;\;\; &\text{condition} \;1\\ &c\geq500K_2 \;\&\&\;K_{2}c\geq20K_w &\text{condition}\;2\\ &c\geq20K_1 &\text{condition}\;3 \end{aligned}

作对数变换得

Pc≤log⁡(500)PK2          condition  1Pc+PK2≤log⁡(20)Kwcondition  2Pc≤log⁡(20)PK1condition  3\begin{aligned} Pc&\leq\log (500)PK_2 \;\;\;\;\;&\text{condition} \;1\\ Pc+PK_2&\leq\log (20)K_w &\text{condition}\;2\\ Pc&\leq\log (20)PK_1 &\text{condition}\;3 \end{aligned}

可见变换后的结果都描述了相空间 R3={  x=(PK1,PK2,Pc)  ∣  PK1,PK2,Pc∈R  }\mathbb{R}^3=\{\;\bm{x}= (PK_1,PK_2,Pc)\;|\;PK_1,PK_2,Pc\in \mathbb{R}\;\} 中一个以平面为边界的区域。将它们和完整的可行域放在一起考虑：

可行域与传统适用条件

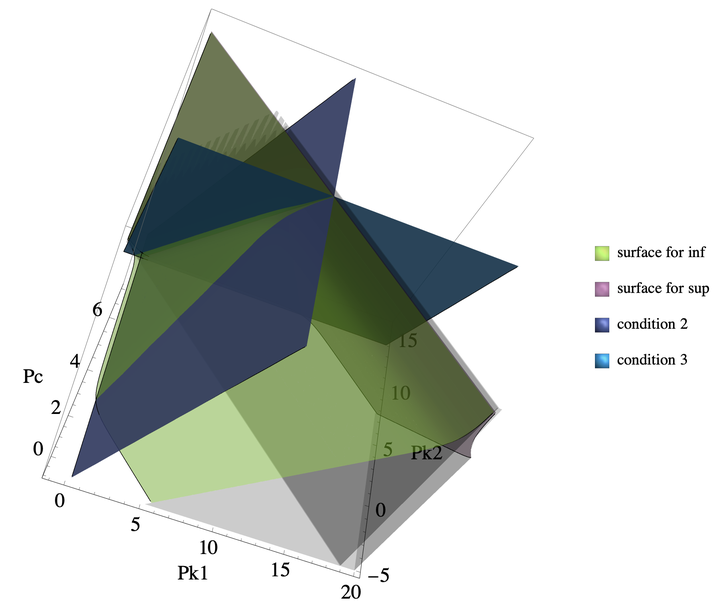
  可见这些限制都具有一定的局限性。现今对于传统条件中 2020 、 500500 等位置的常数更准确的研究即可简化为：寻找可行域边界曲面的最优二元线性拟合函数——在本文提出完整可行域之后便可迎刃而解。在此，作者建议用 10.36510.365来替代条件 Pc+PK2≥log⁡(20)KwPc+PK_2\geq\log (20)K_w 中原本“ 2020 ”的位置。

  代码附于文末，读者可自行尝试。

其他公式

其他可行域

  不难从以上步骤总结出研究计算可行域的一般方法：对数变换 ⇒\Rightarrow 刻画误差 ⇒\Rightarrow 消去 PHPH ⇒\Rightarrow 作图。如法炮制，易得四大公式可行域的边界如下：

四大公式可行域边界

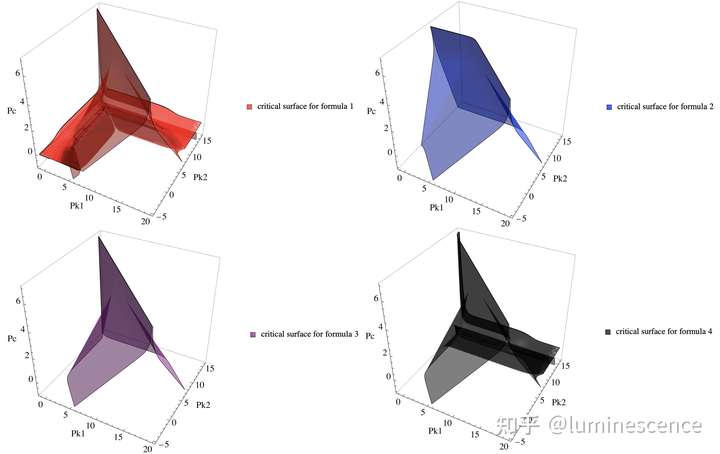
结合公式 f3f_3 的经验以及可行域的实际物理意义，读者不难判断可行域的位置。可以发现，在分析浓度小于 10−610^{-6}的区间，所有近似公式基本完全失效。

最优近似

  由于计算能力的不足，前人对于“哪一个公式在给定误差下的可行域最广？”的问题难以给出明确的回答。然而在计算系统高度发达的当下，找出这一最优公式已是易如反掌。我们借助可视化手段，将四大公式的可行域边界分别重叠：

可行域分别重叠

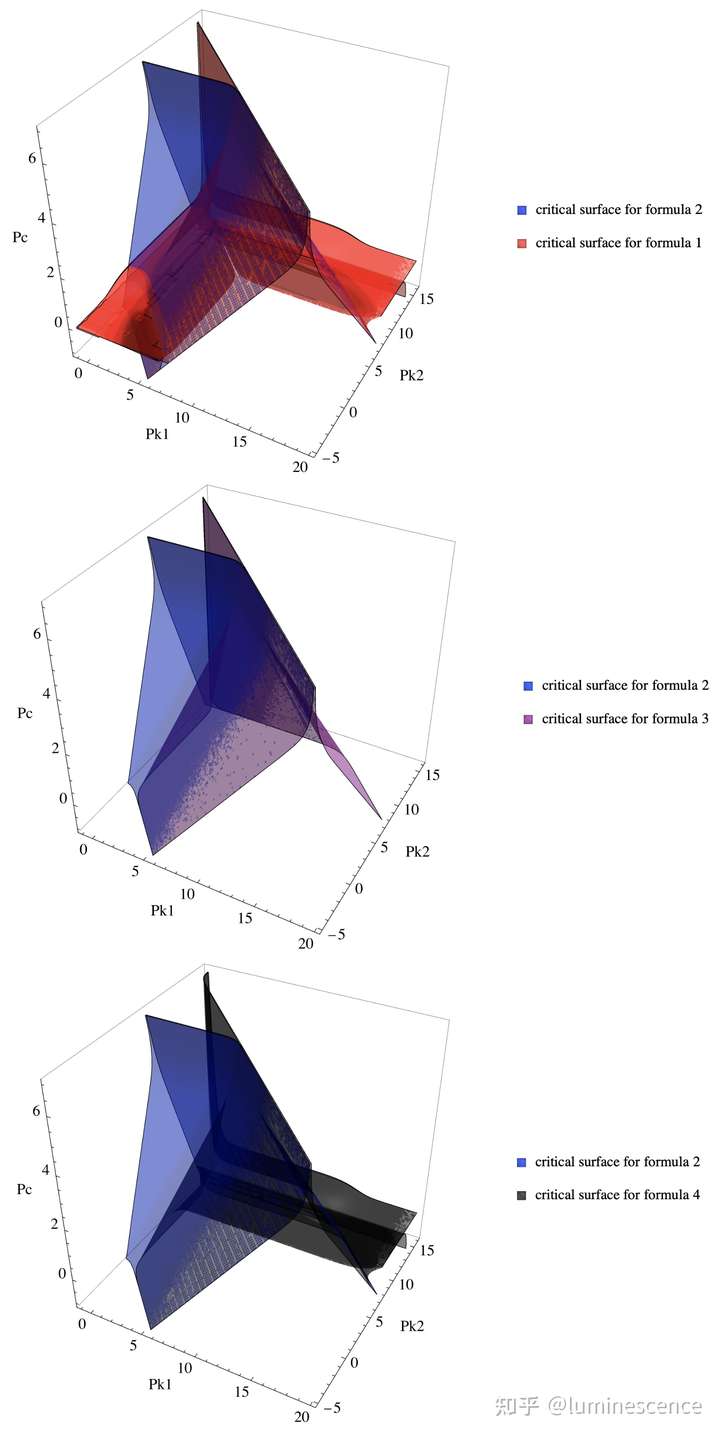
可见公式

[H]x2=K1(c∗K2)c+K1 [H]_{x_2}= \sqrt{ \frac{K_1(c *K_2)}{c+K_1} }

对应的可行域最为宽广。在误差不大于 5%5\% 的标准下的优越性一目了然。

结论

  本文以相对精确结果 [H+][H^+] 偏差 5%5\% 为标准，使用数学方法和计算机手段，引入描述已知条件的 R3\mathbb{R}^3相空间，深刻揭示了 NaHA\text{NaHA} 酸碱度四大近似公式的可行域。希望能为分析化学师生彻底扫除认知障碍。

  对于具体公式的选择问题上，基于可行域空间最宽广的原则，公式

[H]=K1(c∗K2)c+K1[H]= \sqrt{ \frac{K_1(c *K_2)}{c+K_1} }

是其中最优。虽然其他公式有一定的物理意义，但实际效果并不大，剔除之无大碍。

  对于形如 NamHnA\text{Na}_m\text{H}_n\text{A} 的更多元酸式盐，已知条件是 m+n+1m+n+1维向量 $ (PK_1\dots,PK_n,Pc)$，可行域的边界曲面将在高维空间中展开。本文的方法虽然在原则上仍然适用，但略显复杂，需要更多的线性代数知识来辅助处理。如果过程过于复杂，可以参考 EDTA 配位滴定金属离子的处理方式，引入“表观浓度”以简化运算。

交流电和生物电是两种不同的资源，它们应当各得其所。用计算机手段求解化学平衡问题，一定是分析化学课程教学改革的发展方向。

鸣谢

  本文写作得到了中国科学技术大学化学系邵利民副教授的鼎力支持。

  面对一些困难，刘毅凡同学为作者提供了很多帮助和鼓励。

  此外还有来自四面八方的建议，在此一并感谢！

部分代码

  c=0.1c = 0.1下的精确PHPH：

c = 0.1;
accurate = 
ContourPlot3D[
c + 10^-PH == kw/10^-PH + c ((10^-PH*10^-Pk1 + 2*10^-Pk1*10^-Pk2)/
(10^(-2 PH) + 10^-PH*10^-Pk1 + 10^-Pk1*10^-Pk2)), {Pk1, 0, 20}, 
{Pk2, 0, 20}, {PH, 0, 14},PlotTheme -> "Scientific", AxesLabel -> 
Automatic, AxesStyle -> Directive[14], PlotLegends -> {"accurate PH"}, 
PlotRange -> Full]

  特定浓度可行域：

c = 0.1;
    cp3sup = 
    Table[{FindRoot[{c + 10^-(PH - 0.02) == 
    kw/10^-(PH - 0.02) + c ((10^-(PH - 0.02)*10^-Pk1 + 2*10^-Pk1*10^-Pk2)/(
    10^(-2 (PH - 0.02)) + 10^-(PH - 0.02)*10^-Pk1 + 10^-Pk1*10^-Pk2)), 
    PH == 1/2 Pk1 + 1/2 Pk2, Pk2 == a}, {Pk1, 20}, {Pk2, a}, {PH, 20}, 
    WorkingPrecision -> MachinePrecision][[1, 2]], a}, {a, 0, 14, 0.05}];
    
    cp3supline = 
    ListLinePlot[cp3sup, PlotTheme -> "Detailed", PlotStyle -> Orange, 
    FrameLabel -> {{HoldForm[Pk2], None}, {HoldForm[Pk1], None}}, 
    PlotLabel -> HoldForm[c = 0.1 M时公式 Subscript[H, x3] 的可行域], 
    LabelStyle -> {15, GrayLevel[0]}];

    cp3inf = 
    Table[{FindRoot[{c + 10^-(PH + 0.02) == 
    kw/10^-(PH + 0.02) + c ((10^-(PH + 0.02)*10^-Pk1 + 2*10^-Pk1*10^-Pk2)/(
    10^(-2 (PH + 0.02)) + 10^-(PH + 0.02)*10^-Pk1 + 10^-Pk1*10^-Pk2)), 
    PH == 1/2 Pk1 + 1/2 Pk2, Pk2 == a}, {Pk1, 20}, {Pk2, a}, {PH, 20}, 
    WorkingPrecision -> MachinePrecision][[1, 2]], a}, {a, 0, 14, 0.05}];

    cp3infline = 
    ListLinePlot[cp3inf, PlotTheme -> "Detailed", PlotStyle -> Orange, 
    FrameLabel -> {{HoldForm[Pk2], None}, {HoldForm[Pk1], None}}, 
    PlotLabel -> HoldForm[c = 0.1 M时公式 Subscript[H, x3] 的可行域], 
    LabelStyle -> {15, GrayLevel[0]}];

    Show[cp3supline, cp3infline, 
    Graphics[{Thick, Dashed, Orange, Line[{cp3inf[[1]], cp3sup[[1]]}]}], 
    AspectRatio -> 1]

  完整可行域：

cp3infsurface = 
ContourPlot3D[
10^-Pc + 10^-(1/2 Pk1 + 1/2 Pk2 + 0.02) == kw/10^-(1/2 Pk1 + 1/2 Pk2 
+ 0.02) + 10^-Pc*((10^-(1/2 Pk1 + 1/2 Pk2 + 0.02)*10^-Pk1 + 
2*10^-Pk1*10^-Pk2)/(10^(-2 (1/2 Pk1 + 1/2 Pk2 + 0.02)) + 
10^-(1/2 Pk1 + 1/2 Pk2 + 0.02)*10^-Pk1 + 
10^-Pk1*10^-Pk2)), {Pk1, -1, 20}, {Pk2, -5, 16}, {Pc, -1, 7}, 
ContourStyle -> {RGBColor[0.5355579515419151, 0.9430131641554946, 
0.004882822085237493], Opacity[0.5]}, ImageSize -> {500, 500}, 
AxesLabel -> Automatic, AxesStyle -> Directive[Black, 17], 
PlotLegends -> {"surface for inf"}, PlotRange -> Full, 
PlotTheme -> "Scientific", Mesh -> None];

cp3supsurface = 
ContourPlot3D[
10^-Pc + 10^-(1/2 Pk1 + 1/2 Pk2 - 0.02) == 
kw/10^-(1/2 Pk1 + 1/2 Pk2 - 0.02) + 
10^-Pc*((10^-(1/2 Pk1 + 1/2 Pk2 - 0.02)*10^-Pk1 + 2*10^-Pk1*10^-Pk2)/
(10^(-2 (1/2 Pk1 + 1/2 Pk2 - 0.02)) + 10^-(1/2 Pk1 + 1/2 Pk2 - 0.02)
*10^-Pk1 + 10^-Pk1*10^-Pk2)), {Pk1, -1, 20}, {Pk2, -5, 16}, {Pc, -1, 7}, 
ContourStyle -> {RGBColor[0.5864078175768783, 0.26359194937432395`,
0.519486597936422], Opacity[0.5]}, ImageSize -> {500, 500}, 
AxesLabel -> Automatic, AxesStyle -> Directive[Black, 17], 
PlotLegends -> {"surface for sup"}, PlotRange -> Full, 
PlotTheme -> "Scientific", Mesh -> None];

shadow3inf = 
Plot3D[-Log10[(kw/10^-(1/2 Pk1 + 1/2 Pk2 + 0.02) - 
10^-(1/2 Pk1 + 1/2 Pk2 + 0.02))/(1 - ((10^-(1/2 Pk1 + 1/2 
Pk2 + 0.02)*10^-Pk1 + 2*10^-Pk1*10^-Pk2)/(10^(-2 (1/2 Pk1 + 1/2 Pk2 + 0.02)) 
+ 10^-(1/2 Pk1 + 1/2 Pk2 + 0.02)*10^-Pk1 + 
10^-Pk1*10^-Pk2)))], {Pk1, -1, 20}, {Pk2, -5, 16}, 
PlotStyle -> Directive[RGBColor[0.5355579515419151, 0.9430131641554946, 
0.004882822085237493], Opacity[0]], Filling -> Bottom, Mesh -> None, 
BoundaryStyle -> None];

shadow3sup = 
Plot3D[-Log10[(kw/10^-(1/2 Pk1 + 1/2 Pk2 - 0.02) - 
10^-(1/2 Pk1 + 1/2 Pk2 - 0.02))/(1 - ((10^-(1/2 Pk1 + 1/2 Pk2 - 0.02)
*10^-Pk1 + 2*10^-Pk1*10^-Pk2)/(
10^(-2 (1/2 Pk1 + 1/2 Pk2 - 0.02)) + 
10^-(1/2 Pk1 + 1/2 Pk2 - 0.02)*10^-Pk1 + 
10^-Pk1*10^-Pk2)))], {Pk1, -1, 20}, {Pk2, -5, 16}, 
PlotStyle -> Directive[RGBColor[0.5864078175768783, 0.26359194937432395`,
0.519486597936422], Opacity[0]], Filling -> Bottom, Mesh -> None, 
BoundaryStyle -> None];

Show[cp3infsurface, cp3supsurface, shadow3inf, shadow3sup]