树的定义和基本术语
树是$n$个结点的有限集。在任意一颗非空树中:(1)有且仅有一个特定的称为根的结点;(2)当$n>1$时,其余结点可分为m个互不相交的有限集$T_1$,$T_2$,$\dots$,$T_m$,其中
每一个集合本身又是一颗树,并且称为根的子树。
数的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的度(Degree)。度为$0$的结点称为叶子或终端结点。度不为0的结点称为非终端结点或分支结点。除根结点之外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。结点的子树的根称为该结点的孩子(Child),相应的,该结点称为孩子的双亲(Parent)。结点的祖先是从根到该结点所经分支上的所有结点。反之,以某结点为根的子树中的任一结点都称为该结点的子孙。
结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。某双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度(Depth)或高度。
如果将树中结点的各子树看成从左至右是有次序的,则称该树为有序树,否则称为无序树。
森林(Forest)是m棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。由此,也可以森林和树相互递归的定义来描述树。
就逻辑结构而言,任何一棵树是一个二元组$Tree=(root,F)$,其中,$root$是数据元素,称作树的根节点;$F$是$m(m\geq0)$棵树的森林,$F=(T_1,T_2,\cdots,T_m)$,其中$T_i=(r_i,F_i)$称作根$root$的第$i$棵子树;当$m\neq0$时,在树根和其子树森林之间存在下列关系:
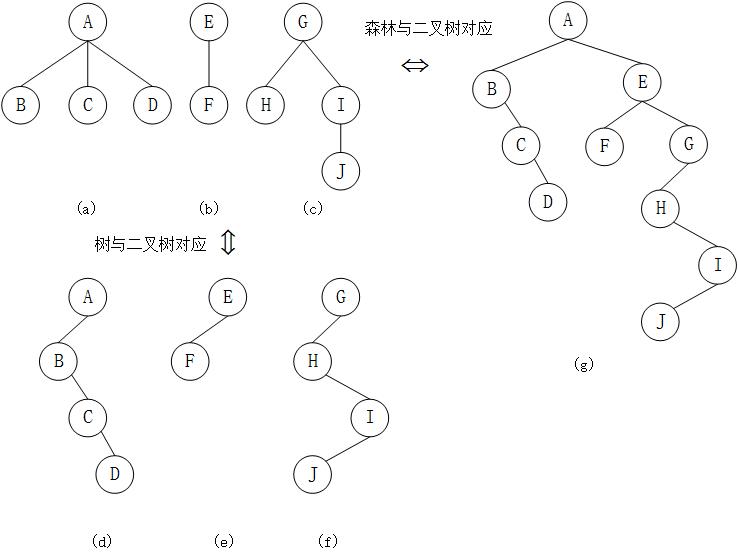
这个定义将有助于得到森林和树与二叉树之间转换的递归定义。
树的应用广泛,在不同的软件系统中树的基本操作集不尽相同。
二叉树
二叉树的定义:
二叉树是另一种树型结构,它的特点是每个结点至多只有两棵子树,而且二叉树的子树有左右之分,其次序不能任意颠倒。
二叉树的性质:
性质一 在二叉树的第$i$层上至多有$2^{i-1}$个结点。
性质二 深度为k的二叉树至多有$2^k-1$个结点。
性质三 对任何一棵二叉树T,如果其终端结点数为$n_0$,度为2的结点数为$n_2$,则$n_0=n_2+1$。
一棵深度为k且有$2^k-1$个结点的二叉树称为满二叉树。
可以对满二叉树的结点进行连续编号,约定编号从根节点起,自上而下,自左至右。由此可以引出完全二叉树的定义。深度为$k$的,有$n$个结点的二叉树,当且仅当其每一个结点都与深度为$k$的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树。这种树的特点是:
(1)叶子结点只可能在层次最大的两层上出现;
(2)对任一结点,若其右分支下的子孙的最大层次是$l$,则其左分支下的子孙的最大层次必为$l$或$l+1$.
完全二叉树的两个重要特性:
性质四 具有n个结点的完全二叉树的深度为$\lfloor\log_2n\rfloor+1$。
性质五 如果对一棵有n个结点的完全二叉树(深度为$\lfloor\log_2n\rfloor+1$)的结点按层序编号(从第1层到第$\lfloor\log_2n\rfloor+1$层,每层从左到右),则对任一结点$i(1\leq i\leq n)$,有:
(1)如果$i=1$,则结点i是二叉树的根,无双亲;如果$i>1$,则双亲PARENT(i)是结点
$\lfloor i/2\rfloor$。
(2)如果$2i>n$,则结点$i$无左孩子(结点i为叶子结点);否则其左孩子LCHILD(i)是结点2i。
(3)如果$2i+1>n$,则结点$i$无右孩子;否则其右孩子RCHILD(i)是结点$2i+1$。
二叉树的存储结构
1.顺序存储结构
#define MAX_TREE_SIZE 100
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;
用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树的结点元素。
2.链式存储结构
二叉树链表:数据域,左指针,右指针,指向双亲结点的指针域
遍历二叉树和线索二叉树
遍历二叉树
先序遍历
若二叉树为空,则空操作;否则
(1)访问根节点
(2)先序遍历左子树
(3)先序遍历右子树
中序遍历
若二叉树为空,则空操作;否则
(1)中序遍历左子树
(2)访问根节点
(3)中序遍历右子树
后序遍历
若二叉树为空,则空操作;否则
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根节点
层序遍历
每一层从左到右访问每一个节点。
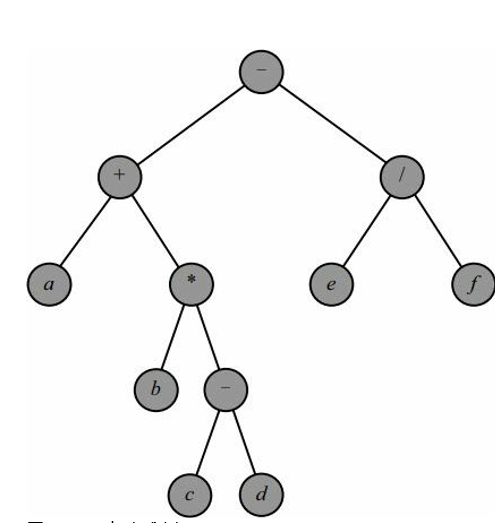
若先序遍历:
若中序遍历:
若后续遍历:
线索二叉树
(作者:简Cloud
链接:https://www.jianshu.com/p/deb1d2f2549a
来源:简书)
遍历二叉树的其实就是以一定规则将二叉树中的结点排列成一个线性序列,得到二叉树中结点的先序序列、中序序列或后序序列。这些线性序列中的每一个元素都有且仅有一个前驱结点和后继结点。
但是当我们希望得到二叉树中某一个结点的前驱或者后继结点时,普通的二叉树是无法直接得到的,只能通过遍历一次二叉树得到。每当涉及到求解前驱或者后继就需要将二叉树遍历一次,非常不方便。
于是是否能够改变原有的结构,将结点的前驱和后继的信息存储进来。
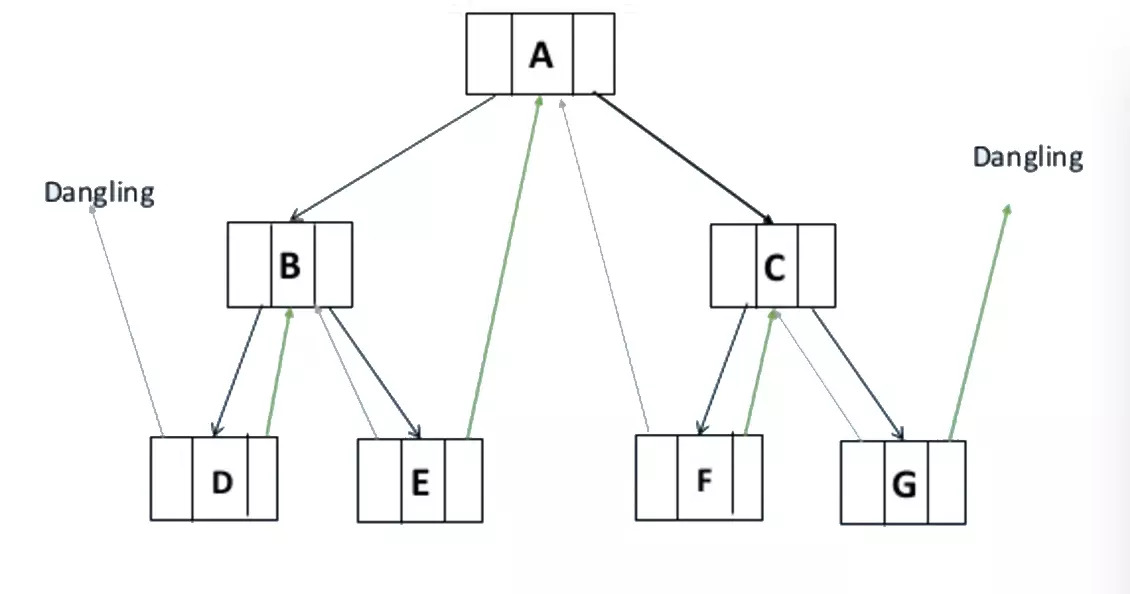
二叉树结构
观察二叉树的结构,我们发现指针域并没有充分的利用,有很多“NULL”,也就是存在很多空指针。
对于一个有n个结点的二叉链表,每个节点都有指向左右孩子的两个指针域,一共有2n个指针域。而n个结点的二叉树又有n-1条分支线数(除了头结点,每一条分支都指向一个结点),也就是存在2n-(n-1)=n+1个空指针域。这些指针域只是白白的浪费空间。因此, 可以用空链域来存放结点的前驱和后继。线索二叉树就是利用n+1个空链域来存放结点的前驱和后继结点的信息。
线索二叉树
如图以中序二叉树为例,我们可以把这颗二叉树中所有空指针域的lchild,改为指向当前结点的前驱(灰色箭头),把空指针域中的rchild,改为指向结点的后继(绿色箭头)。我们把指向前驱和后继的指针叫做线索 ,加上线索的二叉树就称之为线索二叉树。
线索二叉树结点结构
如果只是在原二叉树的基础上利用空结点,那么就存在着这么一个问题:我们如何知道某一结点的lchild是指向他的左孩子还是指向前驱结点?rchild是指向右孩子还是后继结点?显然我们要对他的指向增设标志来加以区分。
因此,我们在每一个结点都增设两个标志域LTag和RTag,它们只存放0或1的布尔型变量,占用的空间很小。于是结点的结构如图所示。

结点结构
其中:
LTag为0是指向该结点的左孩子,为1时指向该结点的前驱
RTag为0是指向该结点的右孩子,为1时指向该结点的后继
因此实际的二叉链表图为
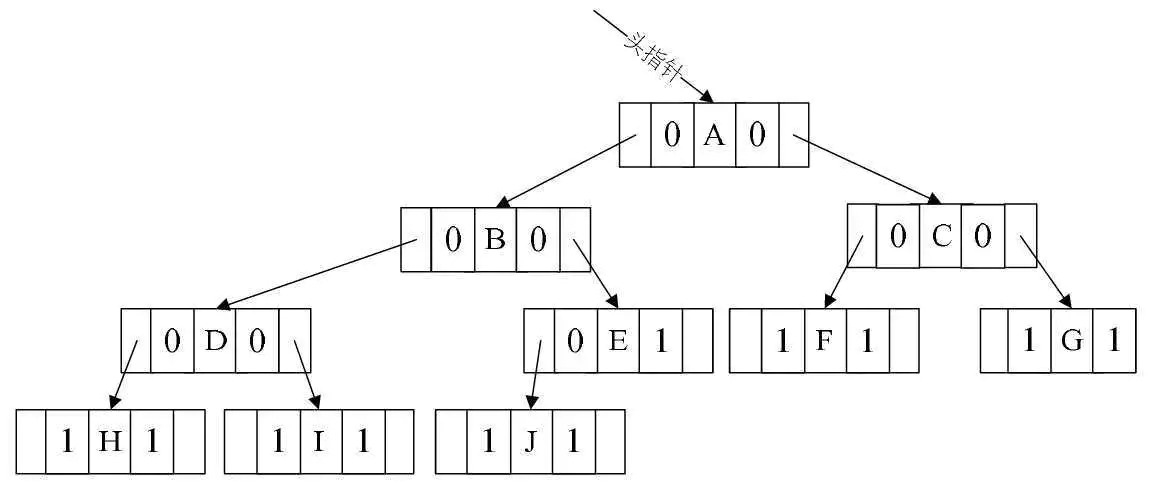
实际的二叉链表图
线索二叉树的结构实现
二叉树的线索存储结构定义如下:
typedef char TElemType;
typedef enum { Link, Thread } PointerTag; //Link==0,表示指向左右孩子指针
//Thread==1,表示指向前驱或后继的线索
//二叉树线索结点存储结构
typedef struct BiThrNode {
TElemType data; //结点数据
struct BiThrNode *lchild, *rchild; //左右孩子指针
PointerTag LTag;
PointerTag RTag; //左右标志
}BiThrNode, *BiThrTree;
二叉树线索化
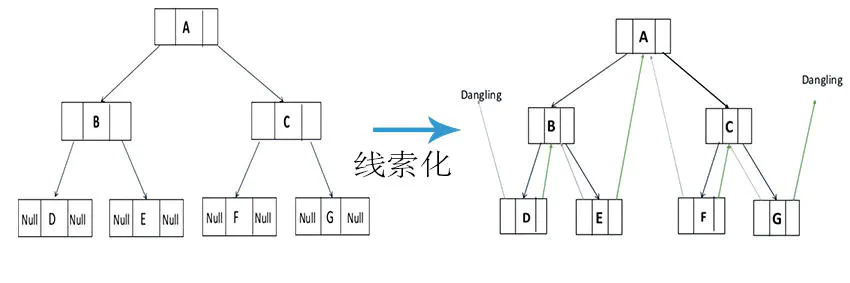
线索化
对普通二叉树以某种次序遍历使其成为线索二叉树的过程就叫做线索化。因为前驱和后继结点只有在二叉树的遍历过程中才能得到,所以线索化的具体过程就是在二叉树的遍历中修改空指针。
线索化具体实现
以中序二叉树的线索化为例,线索化的具体实现就是将中序二叉树的遍历进行修改,把原本打印函数的代码改为指针修改的代码就可以了。
我们设置一个pre指针,永远指向遍历当前结点的前一个结点。若遍历的当前结点左指针域为空,也就是无左孩子,则把左孩子的指针指向pre(相对当前结点的前驱结点)。
右孩子同样的,当pre的右孩子为空,则把pre右孩子的指针指向当前结点(相对pre结点为后继结点)。
最后把当前结点赋给pre,完成后续的递归遍历线索化。
中序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
//--------------------中间为修改空指针代码---------------------
if(!B->lchild){ //没有左孩子
B->LTag = Thread; //修改标志域为前驱线索
B->lchild = *pre; //左孩子指向前驱结点
}
if(!(*pre)->rchild){ //没有右孩子
(*pre)->RTag = Thread; //修改标志域为后继线索
(*pre)->rchild = B; //前驱右孩子指向当前结点
}
*pre = B; //保持pre指向p的前驱
//---------------------------------------------------------
InThreading(B->rchild,pre);
}
增设头结点
线索化后的二叉树,就如同操作一个双向链表。于是我们想到为二叉树增设一个头结点,这样就和双向链表一样,即能够从第一个结点正向开始遍历,也可以从最后一个结点逆向遍历。
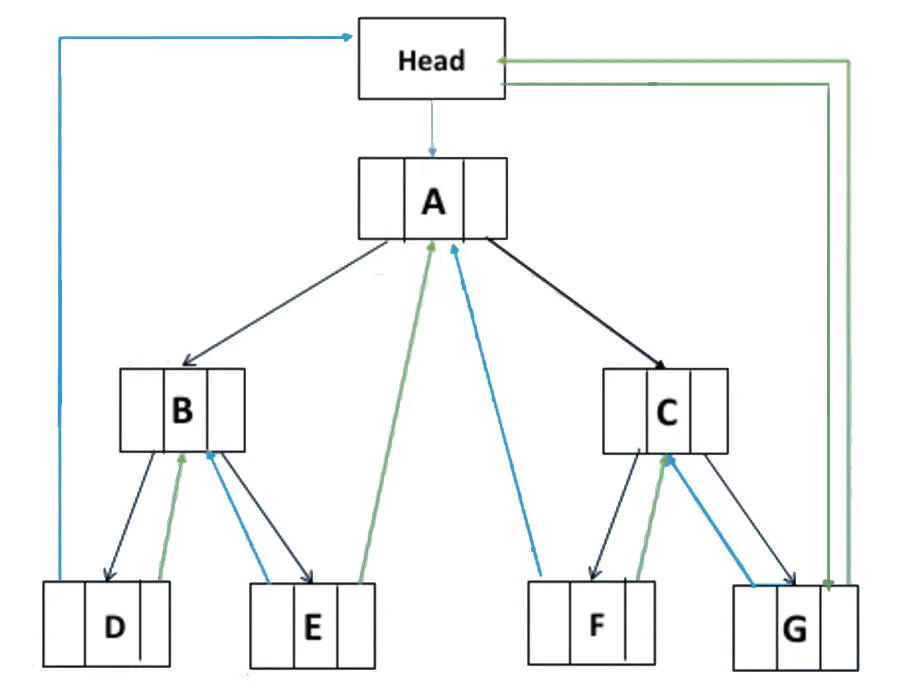
增设头结点
如上图,在线索二叉链表上添加一个head结点,并令其lchild域的指针指向二叉树的根结点(A),其rchild域的指针指向中序遍历访问的最后一个结点(G)。同样地,二叉树中序序列的第一个结点中,lchild域指针指向头结点,中序序列的最后一个结点rchild域指针也指向头结点。
于是从头结点开始,我们既可以从第一个结点顺后继结点遍历,也可以从最后一个结点起顺前驱遍历。就和双链表一样。
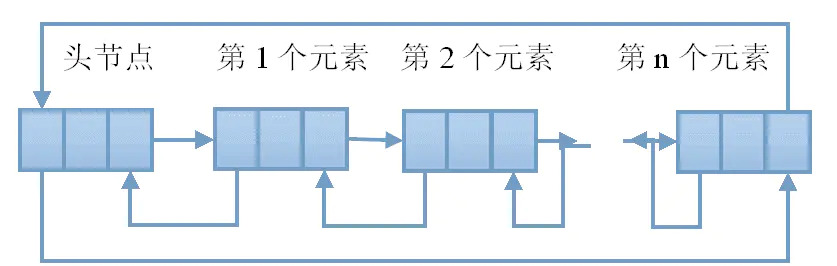
双链表
增设头结点并线索化的代码实现
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW); //开辟结点
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread; //设置标志域
(*Thrt)->rchild = (*Thrt); //右结点指向本身
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre; //设置前驱结点
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
遍历线索二叉树
线索二叉树的遍历就可以通过之前建立好的线索,沿着后继线索依依访问下去就行。
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
完整代码
#include
#include
//函数状态结果代码
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//Status是函数的类型,其值是函数结果状态代码
typedef int Status;
typedef char TElemType;
typedef enum { Link, Thread } PointerTag;
typedef struct BiThrNode {
TElemType data;
struct BiThrNode *lchild, *rchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode, *BiThrTree;
//线索二叉树初始化
Status CreateBiThrNode(BiThrTree * B) {
char ch;
scanf("%c", &ch);
if(ch=='#') *B = NULL;
else{
if(!((*B) = (BiThrNode *)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*B)->data = ch;
(*B)->LTag = Link;
(*B)->RTag = Link;
CreateBiThrNode(&(*B)->lchild);
CreateBiThrNode(&(*B)->rchild);
}
return OK;
}
//线索二叉树线索化
void InThreading(BiThrTree B,BiThrTree *pre) {
if(!B) return;
InThreading(B->lchild,pre);
if(!B->lchild){
B->LTag = Thread;
B->lchild = *pre;
}
if(!(*pre)->rchild){
(*pre)->RTag = Thread;
(*pre)->rchild = B;
}
*pre = B;
InThreading(B->rchild,pre);
}
//为线索二叉树添加头结点,使之可以双向操作
Status InOrderThreading(BiThrTree *Thrt,BiThrTree T){
if(!(*Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))) exit(OVERFLOW);
(*Thrt)->LTag = Link;
(*Thrt)->RTag = Thread;
(*Thrt)->rchild = (*Thrt);
if(!T) {
(*Thrt)->lchild = (*Thrt);
return OK; //若根结点不存在,则该二叉树为空,让该头结点指向自身.
}
BiThrTree pre;
//令头结点的左指针指向根结点
pre = (*Thrt);
(*Thrt)->lchild = T;
//开始递归输入线索化
InThreading(T,&pre);
//此时结束了最后一个结点的线索化了,下面的代码把头结点的后继指向了最后一个结点.
//并把最后一个结点的后继也指向头结点,此时树成为了一个类似双向链表的循环.
pre->rchild = *Thrt;
pre->RTag = Thread;
(*Thrt)->rchild = pre;
return OK;
}
//非递归遍历线索二叉树
Status InOrderTraverse(BiThrTree T) {
BiThrNode *p = T->lchild;
while(p!=T){
while(p->LTag==Link) p = p->lchild; //走向左子树的尽头
printf("%c",p->data );
while(p->RTag==Thread && p->rchild!=T) { //访问该结点的后续结点
p = p->rchild;
printf("%c",p->data );
}
p = p->rchild;
}
return OK;
}
int main() {
BiThrTree B,T;
CreateBiThrNode(&B);
InOrderThreading(&T,B);
printf("中序遍历二叉树的结果为:");
InOrderTraverse(T);
printf("\n");
}
//测试数据:abc##de#g##f###
树和森林
树的存储结构
1.双亲表示法
假设以一组连续空间存储树的结点,同时在每个结点中附设一个指示器指示其双亲结点在链表中的位置,其形式说明如下:

#define MAX_TREE_SIZE 100
typedef struct PTNode{//结点结构
TElemType data;
int parent;//双亲位置域
}PTNode;
typedef struct{//树结构
PTNode nodes[MAX_TREE_SIZE];
int r,n;//根的位置和结点数
}PTree;
2.孩子表示法
孩子表示法存储普通树采用的是 “顺序表+链表” 的组合结构,其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。
如果节点没有孩子节点(叶子节点),则该节点的链表为空链表。

3.兄弟表示法
树结构中,位于同一层的节点之间互为兄弟节点。例如,图 1 的普通树中,节点 A、B 和 C 互为兄弟节点,而节点 D、E 和 F 也互为兄弟节点。
孩子兄弟表示法,采用的是链式存储结构,其存储树的实现思想是:从树的根节点开始,依次用链表存储各个节点的孩子节点和兄弟节点。
因此,该链表中的节点应包含以下 3 部分内容(如图 2 所示):
- 节点的值;
- 指向孩子节点的指针;
- 指向兄弟节点的指针;

森林与二叉树的转换
1.森林转换为二叉树
如果$F={T_1,T_2,\cdots,T_m}$是森林,则可按如下规则转换成一颗二叉树$B=(root,LB,RB)$。
(1)若$F$为空,则$m=0$,则$B$为空树。
(2)若$F$为非空,即$m\neq0$,则$B$的根$root$即为森林中第一棵树的根$ROOT(T1)$;$B$的左子树$LB$是从$T_1$中根节点的子树森林$F_1={T{11},T{12},\cdots,T{1m1}}$转换而成的二叉树;其右子树$RB$是从森林$F’={T_2,T_3,\cdots,T_m}$转换而成的二叉树。
2.二叉树转换为森林
如果$B=(root,LB,RB)$是一棵二叉树,则可按如下规则转换成森林$F={T_1,T_2,\cdots,T_m}$
(1)若$B$为空,则$F$为空。
(2)若$B$为非空,则$F$的第一棵树$T_1$的根$ROOT(T_1)$即为二叉树$B$的根$root$;$T_1$中根节点的子树森林$F_1$是由$B$的左子树$LB$转换而成的森林;$F$中除$T_1$之外其余树组成的森林$F’={T_2,T_3,\cdots,T_m}$是由$B$的右子树$RB$转换而成的森林。
树和森林的遍历
树的遍历:
先根遍历树
后根遍历树
森林的遍历:
先序遍历森林
中序遍历森林
赫夫曼树及其应用
赫夫曼树又叫最优二叉树。
从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径,路径上的分支数目称作路径长度。树的路径长度是从树根到每一个结点的路径长度之和。
若将上述概念推广到一般情况,考虑带权的结点。结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和,通常记作$WPL=\sum_{k=1}^{n}{w_kl_k}$。
假设有$n$个权值${w_1,w_2,\cdots,w_n}$,试构造一棵有$n$个叶子结点的二叉树,每个叶子结点带权为$w_i$,则其中带权路径长度$WPL$最小的二叉树称为最优二叉树或赫夫曼树。
如何构造赫夫曼树?
赫夫曼算法:
1、根据给定的$n$个权值${w_1,w_2,\cdots,w_n}$构成 n棵二叉树的集合$F={T_1,T_2,\cdots.T_n}$,其中每个二叉树$T_i$中只有一个带权为$w_i$的根结点,其左右子树均为空。
2、选择两棵根结点的权值最小的输作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树上的根结点的权值之和。
3、在F中删除这两棵树,同时将新得到的二叉树加入F中。
4、重复2和3,直到$F$只含一棵树为止。这棵树便是赫夫曼树。
赫夫曼编码
前缀编码:任意一个字符的编码都不是另一个字符的编码的前缀,这种编码叫前缀编码。
设计电文总长最短的二进制前缀编码即为以n种字符出现的概率作权,设计一棵赫夫曼树的问题,由此得到的二进制前缀编码便成为赫夫曼编码。