工程实现

科学技术原理

三体问题经典的二体问题的一般化——二体问题是研究两个物体的运动方程。

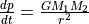
来看牛顿万有引力定律： {dp \over dt}={G{M_1M_2}\over{r^2}}

其中，p是动量,t是时间，G是重力常数，m1 和m2 是质量，r是物体之间的距离。

在大多数情况下可以假定物体质量不变。因此，来自N-1个其他物体的第i个物体上的力如下:

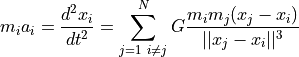
m_ia_i={d^2x_i\over dt^2}=\sum^{N}_{j=1 \ i\neq j}{G\frac{m_im_j(x_j-x_i)}{|| x_j - x_i||^3}}

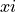xi 是第i个物体的位置。根据各个物体的质量和位置，可以计算加速度 a_i :

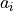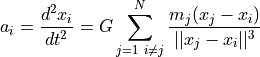
a_i={d^2x_i\over dt^2}=G\sum^{N}_{j=1 \ i\neq j}{\frac{m_j(x_j-x_i)}{|| x_j - x_i||^3}}

将这个加速度带入标准的时间离散运动方程：1

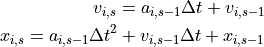
v_{i,s}=a_{i,s-1}\Delta t+v_{i,s-1} x_{i,s}=a_{i,s-1}\Delta t^2+v_{i,s-1}\Delta t+x_{i,s-1}

其中v是速度，s是分段的时间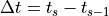，\Delta t= t_s -t_{s-1} 是时间间隔的长度。

给定所有N个物体的初始条件 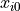x_{i0} 以及时间间隔Δt ，这些方程将数值求解物体未来的位置、速度、加速度。现在有了数学物理原理的离散实现，理论问题解决后 以下就是工程问题的设计方案

设计方案

为实现三体运动数值计算的数值计算和可视化，用 numpy 作为主要的数据结构存储质点的位置，速度，时间以及质量， 引力常数，时间微分等等信息，为实现数据的可复用性，使用 csv(符号分割符) 来保存信息。

可视化实现方面使用 pyqtgraph 和 PyQt5 的结合使用， pyqtgraph 用于3D数据的呈现, PyQt5 用于实现控件 以及事件的触发及处理。例如参数设置的表格由 PyQt5 实现，而参数的计算结果以散点运动和轨迹连线的结果由 pyqtgraph 表现.

创新性体现

相比于单纯数值计算的输入输出实现，采用 pyqtgraph 的强大3D功能可以使三体运动更加直观,虽然用matplotlib也可以实现3D 绘图，但是其拓展性和绘制速度难以与C++底层实现的Qt以及OpenGL渲染速度相媲美。此外，对参数的设置以及结果数据的保存，打开 方式可以提高数据复用性和规范性，可以满足不同设备上的交流需求。界面设置上尽可能提供用户设置的自由度，如散点大小，颜色，轨迹， 时间微分甚至引力常数和质量，也可以调节刷新速度，使使用方式更加具有趣味性。

运行方法和操作实现

在安装PyQt5,pyqtgraph,matplotlib,numpy,csv的环境下，可在文件所在目录的命令控制行下输入

>>> python ThreeBodyProblem.py

打开图形界面，点击“参数设置”，依次填写质点信息，点击“视图”选项，在弹出的颜色选项框中选择颜色，以此应用于散点颜色以及轨迹。

以上参数设置完毕后，点击“暂停/运动”按钮，如果移动现象不明显，可以拖动speed选择条，或者用滚轮放大3D视图使得运动更加明显，

在3D视图中使用鼠标左键拖动实现旋转，按住键盘“ctrl”+鼠标左键拖动实现坐标平移。

注意：平移后再次旋转可能会导致视图混乱，此时可以点击“摄像机归位”，回复初始观察状态。

点击单选框可以切换是否显示轨迹，“ctrl+s”可以保存当前数据文件。 请注意保存的csv文件可以用记事本或VScode编辑,如果用Excel仅适合观查数据，不要在Excel中编辑数据！否则可能导致程序无法再次读取信息。

1

Python物理学高效计算 (安东尼·斯科普斯)