10.11主要内容

上节课补遗

Nogaosa书上两处补充Nagaosa_17, Nagaosa_26

不同场的量子化典型模型与量子化条件

不同场的量子化典型模型与量子化条件

量子化条件(quantization conditions)

$\left[x,p\right]=i\hbar$;
$\left[\psi(x),\psi^{\dagger}(x')\right]=\delta(x-x')$;
$\left[\psi(x),\pi(x')\right]=i\hbar \delta(x-x')$;
$\left[\psi(x),\dot{\psi}(x')\right]=i\hbar \delta(x-x')$
$\left[A,E\right] \propto i\hbar \delta(x-x')$

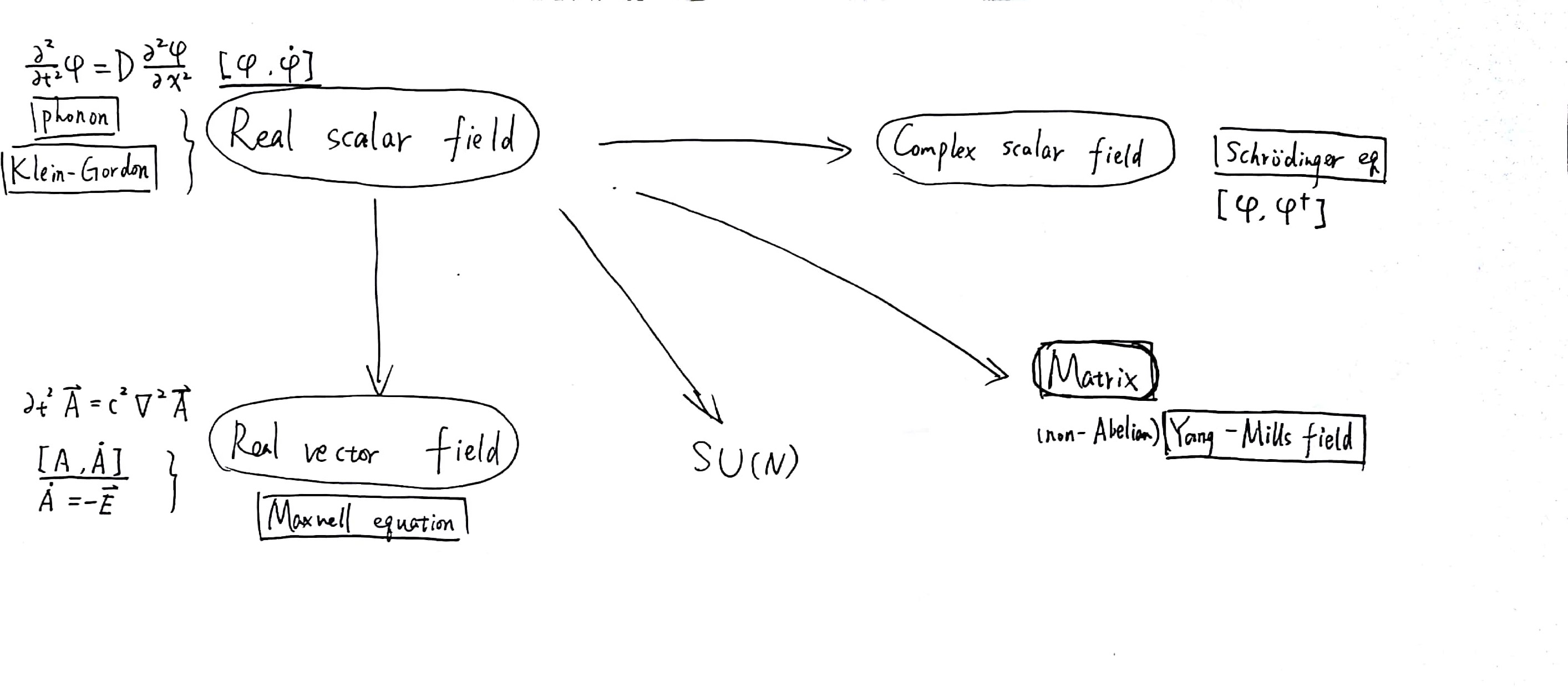
实标量场的量子化（phonon field, Klein-Gordon equation）

1. Einstein&Debye heat capacities Heat capacities of solids 原文下载

复标量场的量子化（Shrodinger equation）

矢量场的量子化（电磁场的Maxwell equations）

1. Astrid Lambrecht, 2002 The Casimir effect: a force from nothing[J]. Physics world, 15(9): 29. 原文下载

第四次课总结

• 总结
  1. 为什么波函数可以被量子化？波函数量子化的本质与$\left[x,p\right]=i\hbar$不同吗？
     A: 二者的本质是相同的，波函数之所以能量子化，还是来源于基础的不对易关系$\left[x,p\right]=i\hbar$，这一点在phonon场中可以看得很清楚。
  2. 以phonon场为例的作用:
     1. 诠释了所有量子化的本质
     2. 揭示出了连续模型与离散模型之间的对应关系：$\phi(ia)=x_i$, 本质上就是在该点处偏移平衡位置的位移量。
     3. 引入了一些计算技巧
        与$(x, p)$关系的类比性
        形如$\psi=\sum \frac{1}{\sqrt{2m\omega_k}}\left( a_k e^{i(kx-\omega_k t)} - a_{k}^{\dagger} e^{-i(kx-\omega_k t)}\right)$，可令$b_k=a_k e^{i(kx-\omega_k t)}, b_{k}^{\dagger}=a_{k}^{\dagger} e^{-i(kx-\omega_k t)}$简化计算

USTC| BBS