matlab学习

1.matlab基础

1.1基本数据类型

1.1.1整数

非整数要想转换成整数可以使用int8()、int16()、int32()、int64()、以及uint64()等进行转换。

下面是几种取整函数：

round()四舍五入、floor()向下取整、ceil()向上取整。

1.1.2双精度浮点型

matlab默认是使用双精度浮点型，占用8个字节长度，其中第63为是符号位，0到51位表示小数部分，52位到62位表示指数部分。

1.1.3复数

可以直接采用赋值语句（i或j）产生复数，也可以使用complex(a,b)，产生a为实部、b为虚部的复数。

real(z)得到实部、imag(z)得到虚部、abs(z)得到模、angle(z)得到弧度制下的角度、conj(z)得到共轭复数。

1.1.4format函数改变数据的显示格式

注意：format函数仅仅是改变数据的显示格式，不会改变数据的值。默认是format short，即保留小数点后四位，还有其他格式（比如显示小数点后更长的位数、分数形式以及科学计数法）可以用help命令查看文档，help format。

format rational比较常用以分数的形式显示。

1.1.5逻辑型

true和false分别代表逻辑真和假，matlab中真假分别用1和0表示。true(3,4)表示生成一个3行4列的逻辑值数组。

可以使用logical()函数将一个数值转换成逻辑型。

1.1.6字符型数据类型

在matlab中不区分字符和字符串，都用char表示，都用单引号括起来，matlab支持中文字符。

1.1.7函数句柄类型

函数句柄也是一种数据类型。例如f = @cos，可以通过创建函数句柄来实现对函数的间接调用。f(3.1415)输出为：-1。

1.1.8单元数组

采用大括号来创建一个单元数组，如a = {'中国','China';[1,2,3,4,5],100}

单元数组支持下标索引，索引从1开始，如a{1,1}表示访问第一行第一列的元素。也可以用索引的方式为单元数组的元素赋值。

c = cell(3,4)表示创建一个单元数组，之后可以用索引的方式为单元数组的元素赋值。

celldisp(c)显示单元数组所有元素的值。

cellplot(c,'legend')可以以彩色图形的方式展示一个单元数组。

单元数组转结构体，s = cell2srtuct(c,fields,2)，其中c为单元数组，fields为结构体内的成员变量名，2表示维度。用的时候可以用：help 查看具体的语法细节。

1.1.9结构体

可以直接用点号来给一个结构体变量赋值，比如：str.name = 'zhang',str.age = 18;其中str为结构体变量名，也可以起其他变量名。str(1).name = 'zhang',str(2).name = 'Li';这样就创建了一个结构体数组，str为1行2列。

1.2运算符

1.2.1基本运算符

matlab的基本运算符包括有+、-、*、/左除（我们一般意义上的除法）、\右除（前面是除数后面是被除数）、^幂运算、‘转置。在进行矩阵运算时，前面加点表示对应元素进行运算，前面没有点号则进行矩阵的加减乘除。

1.2.2关系运算符

关系运算符返回bool，注意matlab的不等于是~=，当关系运算符两边都是向量或矩阵时，维度必须相等，否则报错。

另外几个小技巧：

1.判断两个浮点数是否相等，因为浮点数有精度问题，直接比较容易得到错误结果，故采用abs(a-b) <1e-10的方式来进行比较。

2.筛选矩阵中满足条件的元素，result = A>0.5，矩阵A中大于0.5的元素返回1，其余是0。

1.2.3逻辑运算符

与、或、非。符号表示为：&、|、~。函数表示为：and、or、not、xor异或。比如：and(1,0)返回0，or(1,0)返回1。

还有个快速逻辑与、快速逻辑或，它与上面的区别是：当判断第一个操作数可以决定整体逻辑时，不再往下进行运算，比如0&&1，当第一个操作数为0时无论后面怎么样，结果一定是0，就不往下进行运算了。

按位逻辑运算符：按位与：bitand(a,b)，传入的a和b都是十进制数，先转换成二进制，再对每一位进行逻辑运算，最后得到一个二进制数，转换成十进制即为返回的结果。同样还有按位或bitor(a,b)、按位非bitnot(a)、按位异或bitxor(a,b)。

1.3matlab中的常量和变量

matlab中默认的常量有：

inf表示无穷的，当一个数大于2^1024时就被认为是无穷大了。
pi 表示圆周率3.1415...
ans 默认变量名，返回最后一次运算的结果
eps浮点数的相对误差
realmax最大正实数、realmin最小正实数
i或j复数单位
NAN不定值

matlab变量命名规则：

不超过31个字符
字母开头，由字母、数字、下划线组成
区分大小写

2.向量和矩阵分析

2.1创建向量

2.1.1一般方法创建

方括号包裹，逗号分割表示在一行，分号分割表示另起一行。索引下标从1开始。

2.1.2用冒号来进行创建

a = 1:9表示创建一个行向量1到9
a = 1:2:9表示创建一个行向量1、3、5、7、9。中间2表示间隔
间隔可以为负，如：a = 9:-2:1表示创建行向量9、7、5、3、1

2.2创建矩阵

2.2.1一般方法创建

方括号包裹，逗号分割表示在一行，分号分割表示另起一行。索引下标从1开始。

2.2.2拼接

比如：A和B是两个3行3列的矩阵

[A,B]是横向拼接，得到3行6列的矩阵

[A;B]是纵向拼接，得到6行3列的矩阵

还有几个拼接的函数：

C = vertcat(A,B)纵向拼接，矩阵A、B的列数必须相同
C = horzcat(A,B)横向拼接，矩阵A、B的行数必须相同

2.2.3生成

常见的生成方法：

全0矩阵。zeros(3,4)生成3×4全0矩阵，zeros(3)生成3阶全0矩阵，zeros(size(B))生成和B一样尺寸的全0矩阵
全1矩阵。ones(3,4)生成3×4全1矩阵，ones(3)生成3阶全1矩阵，ones(size(B))生成和B一样尺寸的全1矩阵
单位矩阵。eye(3)生成3阶单位矩阵，eye(3,4)生成3×4对角线上元素为1的矩阵，eye(size(B))生成和B一样尺寸的对角线上元素为1的矩阵
魔术矩阵。magic(3)生成3阶魔术矩阵
均匀随机数矩阵。rand(3,4)生成3×4元素为0到1均匀分布随机数的矩阵，如果要得到0到5均匀分布随机数的矩阵，先得到0到1的再乘以5即可
标准正态随机数矩阵。randn(3,4)生成3×4元素为标准正态分布随机数的矩阵
范德蒙矩阵，通过vander(V)生成以向量V为基础的范德蒙矩阵。范德蒙矩阵：矩阵最后一列全为1，倒数第二列为指定的向量，其他各列是其后列与倒数第二列的点乘积。
希尔伯特矩阵，通过hilb(n)来生成n阶希尔伯特矩阵。希尔伯特矩阵：当矩阵中的任何一个元素发生一个微小变化时，整个矩阵的值以及其逆矩阵都发生巨大的变化。通过invhilb(n)来生成n阶希尔伯特矩阵的逆矩阵。
托普利兹矩阵，通过toeplitz(x,y)生成托普利兹矩阵。托普利兹矩阵：以x向量为第一列，y向量为第一行，除第一行和第一列外，其他元素都与其左上角的元素相同的矩阵。toeplitz(x)相当于toeplitz(x,x)此时托普利兹矩阵是对称的。注意x和y的第一个元素必须相同。
伴随矩阵，通过函数compan(p)产生伴随矩阵，p为多项式的系数向量，高次幂在前、低次幂在后
帕斯卡矩阵，通过函数pascal(n)产生n阶帕斯卡矩阵。二次项展开后的系数随n的增大组成一个三角形表，称为杨辉三角，由杨辉三角组成的矩阵叫帕斯卡矩阵。

2.2.4块复制操作

1.通过函数repmat()，A = repmat(B,m,n)表示将B看作单个对象，生成一个m行n列的大矩阵，A = repmat(B,m)表示将B看作单个对象，生成一个m行m列的大矩阵。

2.通过函数blkdiag(),A = blkdiag(B,C...)生成一个B、C...构成的准对角矩阵。

2.2.5导入

比如：通过函数imread()读取图片，得到图像数据的二维矩阵。

2.2.6矩阵的注意事项

矩阵是按列来进行存储的，索引时要注意，例如：A = [1,2,3;4;5;6]。A(2)返回的是4，A(2,3)返回第2行第3列的元素6。

矩阵的下标索引支持所谓的切片操作，A(1:end,end)可以获取最后一列，运用好切片操作可以很灵活的得到分割后的矩阵。

2.3向量和矩阵的运算

2.3.1基本算术运算

注意：

在进行向量和矩阵运算时，前面加点表示对应元素进行运算，前面没有点号则进行向量和矩阵的加减乘除。
注意运算的维度，维度正确才可以计算。
矩阵和标量进行运算，比如：矩阵A-2表示矩阵的每个元素都减2，A*2表示矩阵的每个元素都乘以2
不要轻易用矩阵的除法，一般都能转化成求逆再相乘

2.3.2关系运算

前面讲过，主要是一些技巧

筛选矩阵中满足条件的元素，result = A>0.5，矩阵A中大于0.5的元素返回1，其余是0。
将满足条件的元素赋值A(A>0.5) = 100，将A中大于0.5的元素赋值为100

2.3.4逻辑运算

一些技巧：

A&B，两个矩阵必须同规格，对应位置上的元素，两个只要有一个为0，则返回的新矩阵对应位置元素为0
同样还有相或的运算

2.4向量和矩阵的信息获取

2.4.1判断函数

介绍一些常见的判断函数函数：

isempty()检测是否为空
isscalar()检测是否为标量
isvector()检测是否为向量
isrow()检测是否为行向量
iscolum()检测是否为列向量
issparse()检测是否为稀疏矩阵

2.4.2尺寸函数

size()返回二维数组的行数和列数。

length()返回一维数组的长度，如果是二维数组返回max(行数,列数)

ndims()返回数组的维数

也可以用一行命令whos来查看所有的变量，whos给出的信息很多，有类型、大小、占用字节数等等。

2.4.3查找函数find()，非常常用

find()函数，括号内放逻辑表达式，返回逻辑表达式为真对应元素的下标。

find(A>0.5)，返回A中大于0.5的元素所在下标，常用于给满足条件的元素进行赋值操作，非常常用。

直接find(A>0.5)返回单下标。[i,j] = find(A>0.5)返回双下标，i为行，j为列。

如果有多个下标符合，则返回的是这些下标组成的列向量。

2.5矩阵的其他操作

2.5.1矩阵中元素的删除

用的最多的的是采用空矩阵[]的方法进行删除操作

A([1 3],:) = [] ，表示删除矩阵的第一行和第三行

A(:,end) = [] ，表示删除矩阵的最后一列

2.5.2矩阵的转置

常用的方式是使用 ’ 来进行转置，但是如果矩阵中含有复数时，得到的其实是先转置再共轭的结果。

使用transpose(A)来进行转置，是真正的转置，即便矩阵有复数存在，也不会进行共轭操作。

2.5.3矩阵的旋转

rot90(A)将矩阵逆时针旋转90°

rot90(A,k)将矩阵逆时针旋转k × 90°

2.5.4矩阵的翻转

fliplr(A)进行左右翻转。flipud(A)进行上下翻转。

filpdim(A,1)相当于flipud(A)，filpdim(A,2)相当于fliplr(A)。

2.5.5矩阵尺寸的改变

B = reshape(A,m,n)实现尺寸的改变，本质分为两步，先将矩阵展开（注意是先列后行）成向量，向量再生成矩阵（仍是先列后行）。

2.5.6矩阵的排序函数sort()

一般来说，是升序排序。添加’descend‘可变为降序。

如果传入的是一个一维的向量，毫无疑问直接排序，如果传入的是一个二维矩阵，那么默认情况下，会按列为单位进行操作（每一列都作为一个向量进行sort，之后把这些排好序的列合成原尺寸的矩阵）；若指定dim = 2即sort(A,2)，则按行为单位进行操作。

sort(A,2,'descend')表示按行为单位进行操作，且降序。

2.5.7矩阵元素的求和

sum(A)函数，对矩阵的每列求和返回一个行向量。

cumsum(A)函数。累计求和，也是按列为单位进行，返回与原来尺寸相同的矩阵。

它们都有一个dim参数，当dim值为2时，按行进行。比如：cumsum(A,2)表示以行为单位进行累计求和。

如果要求所有元素的和，则用sum(sum(A))。sum()函数，当参数为行向量或列向量时，返回行或列求和的结果。

2.5.8矩阵元素的求积

与上面的求和类似，只不过将函数名换作prod和cumprod。

2.5.9矩阵元素的差分

B = diff(A)以列为单位求一阶差分

B = diff(A,N)以列为单位求N阶差分

B = diff(A,N,2)以行为单位求N阶差分

2.6矩阵和线性代数

2.6.1方阵的行列式

通过函数det(A)，来求一个方阵的行列式。

2.6.2特征值、特征向量和特征多项式

eig(A)函数。

E = eig(A)：求矩阵A的全部特征值，组成向量E。

[V,D] = eig(A)：方阵V的每一列为一个特征向量，方阵D为对角矩阵，对角线上的每一个元素为特征值（特征值在对角线上按照从小到大的顺序排列）。

知识拓展：前面介绍了伴随矩阵，p为多项式的系数向量，高次幂在前、低次幂在后。A = compan(p)，再解得A的特征值即为多项式方程的根。

2.6.3对角矩阵

diag(A)获取矩阵A主对角线上的元素，组成一个列向量。

diag(A,k)获取矩阵A第k条对角线上的元素，组成一个列向量。主对角线k=0，之后第一条对角线指主对角线右上方的第一条对角线，第k条类似推。

2.6.4上三角矩阵和下三角矩阵

上三角矩阵，对角线左下方的所有元素都为0；下三角矩阵，对角线右上方的所有元素都为0。

triu(A)获取上三角矩阵

triu(A,k)获取第k条对角线（包括）之后的上三角矩阵

tril(A)获取下三角矩阵

tril(A,k)获取第k条对角线（包括）之后的下三角矩阵

2.6.5矩阵的逆和伪逆（伪逆也叫广义逆矩阵）

inv(A)求矩阵A的逆矩阵

pinv(A)求矩阵A的广义逆矩阵。

知识拓展：广义逆矩阵：如果A不是一个方阵或者是一个非满秩的方阵时，它没有逆矩阵，但是可以找到一个与A的转置同型的矩阵B满足

A×B×A = A
B×A×B = B

此时称B为A的伪逆，也叫广义逆矩阵。

2.6.6矩阵的秩

rank(A)求矩阵A的秩

2.6.7矩阵的Jordan标准型

J = jordan(A)，求约当标准型J。

[V,J] = jordan(A)，得到的V和J满足：J = V^-1*A*V

2.6.8矩阵的迹

trace(A)求矩阵A的迹。

矩阵的迹等于对角线元素之和，也等于其特征值之和。

2.6.9矩阵的范数

norm(A)或norm(A,2)求矩阵A的2阶范数，即矩阵的最大奇异值。

norm(A,1)求矩阵A的1阶范数，即矩阵的列向元素和的最大值。

norm(A,inf)求矩阵A的无穷阶范数，即矩阵的行向元素和的最大值。

norm(A,'fro')求矩阵A的Frobenius范数。

2.6.10矩阵的标准正交基

通过函数orth()求一个矩阵的标准正交基。

B = orth(A)，矩阵B的列向量组成了矩阵A的一组标准正交基。

2.6.11矩阵的超越函数

sqrtm(A)用于计算矩阵的平方根

logm(A)用于计算矩阵的自然对数

expm(A)用于计算矩阵的指数

funm(A,@sin)用于计算矩阵的超越函数值，第二个参数用于指定函数的句柄

2.7稀疏矩阵

2.7.1如何产生一个稀疏矩阵

有以下几种方式：

可以通过函数sparse(A)将一个普通的矩阵转化为稀疏矩阵。
S = sparse(m,n)产生一个m行n列，所有元素都为0的稀疏矩阵。
S = sparse(i,j,v,m,n)。根据 i、j 和 v 三元组生成稀疏矩阵 S，其中 S(i(k),j(k)) = v(k)，并且矩阵的尺寸为m×n。
产生一个稀疏单位矩阵，可以用speye(n)、speye(m,n)

2.7.2稀疏矩阵其他相关函数

full(A)将一个稀疏矩阵转化为普通矩阵。

nnz(A)计算稀疏矩阵中非零值的个数。

spy(A)对稀疏矩阵中非零元素的分布进行图形化的显示。

issparse(A)判断一个矩阵是否为稀疏矩阵。

nonzeros(A)矩阵中非零元素值。

syones(A)将稀疏矩阵中的非零元素替换为1

2.8矩阵的分解

2.8.1Cholesky分解

对于正定矩阵，可以分解为上三角矩阵和下三角矩阵的乘积，这种分解叫做Cholesky分解。能够进行Cholesky分解的矩阵必须是正定的，矩阵的所有对角元素必须是正的，同时矩阵的非对角元素不能太大。

通过chol()函数进行矩阵的Cholesky分解。B = chol(A)，则B‘*B = A。

2.8.2LU分解

将方阵A分解为下三角矩阵的置换矩阵L和上三角矩阵U的乘积。

[L1,U1] = lu(A)将矩阵分解为下三角矩阵的置换矩阵L1和上三角矩阵U1。A = L1*U1。

[L2,U2,P] = lu(A)将矩阵分解为下三角矩阵L2和上三角矩阵U2，以及置换矩阵P。

2.8.3QR分解

QR分解将一个m行n列的矩阵A分解为一个正交矩阵Q（m行m列）和一个上三角矩阵R（m行n列）的乘积。

[Q,R] = qr(A)，则Q*R = A。

2.8.4SVD分解（奇异值分解）

S = svd(A)，对矩阵A进行奇异值分解，返回由奇异值组成的列向量，奇异值按照从小到大的顺序排列。

[U,S,V] = svd(A)，对矩阵A进行奇异值分解，其中U和V为酉矩阵，S为一个对角矩阵，对角线元素为矩阵的奇异值的降序排列。

奇异值分解有：A = U*S*V'

2.8.5Schur分解

A = U*S*U'，矩阵A必须是方阵，U为酉矩阵，S为块对角矩阵。

[U,S] = schur(A)得到酉矩阵U和块对角矩阵S。

S = schur(A)得到块对角矩阵S。

2.8.6Hessenberg分解

对于任意一个n阶方阵都可以进行Hessenberg分解，分解公式为A = P*H*P'，其中P是酉矩阵，H的第一子对角线下的元素均为0即H为Hessenberg矩阵。

H = hess(A)，返回Hessenberg矩阵。

[P,H] = hess(A)，返回P和H，满足A = P*H*P'。

3.多项式、插值和极限

3.1多项式及其函数

3.1.1多项式的建立

多项式的系数按照降幂的次序存放在向量中，称为多项式的系数向量。

下面给出几种多项式的建立方式：

通过多项式系数向量p来建立，y = poly2sym(p)
通过多项式的根来建立，分为两步，先定义根向量r，然后p = poly(r)转换成系数向量p，最后y = poly2sym(p)

3.1.2多项式的求值与求根

多项式求值：

polyval(p,A)，以数组或矩阵中的元素为计算单位
polyvalm(p,A)，以矩阵为计算单位，用于求矩阵多项式

多项式求根：

利用roots(p)求取多项式的根。

已知多项式的根求多项式的系数：

先定义根向量r，然后p = poly(r)转换成系数向量p。

3.1.3多项式乘法

多项式乘法：

c = conv(a,b)，其中a和b分别为两个多项式的系数向量，c是相乘结果的系数向量。

3.1.4多项式的导数和积分

多项式的导数：

polyder(p)，对以p为系数向量的多项式求导，返回求导后的多项式系数向量
polyder(a,b)，其中a和b分别为两个多项式的系数向量，先将a和b对应的多项式相乘，再返回求导结果的系数向量
[q,d] = polyder(b,a)，其中a和b分别为两个多项式的系数向量，先将a和b对应的多项式相除（b/a），再返回求导结果的系数向量（q/d）

多项式积分：

polyint(p)，对多项式进行积分运算，返回求导后的多项式系数向量，默认积分常数是0
polyint(p,k)，对多项式进行积分运算，返回求导后的多项式系数向量，积分常数是k

3.1.5多项式展开

部分分式展开：

[r,p,k] = residue(b,a)，求多项式之比b/a的部分分式展开。其中r、p、k对应的系数向量如下：

a(x)对应的多项式无重根：

\frac{b (x)}{a (x)} = \frac{r_{1}}{x - p_{1}} + \frac{r_{2}}{x - p_{2}} + . . . + \frac{r_{n}}{x - p_{n}} + k_{s}

a(x)对应的多项式有重根：

\frac{b (x)}{a (x)} = \frac{r_{1}}{x - p_{1}} + \frac{r_{2}}{(x - p_{1})^{2}} + . . . + \frac{r_{n}}{(x - p_{1})^{n}}

3.1.6多项式拟合

利用p = polyfit(x,y,n)对给定数据进行多项式拟合，x和y为数据的坐标组成的向量，n为拟合的多项式次数，返回系数向量。

拟合还可以在figure窗口下的工具栏，直接进行图形化用户操作。

3.2插值

3.2.1一维插值

利用函数interp1()进行一维多项式插值。

利用函数interpft()进行一维快速傅里叶插值。

3.2.2二维插值

利用函数interp2()进行二维插值，函数相关的参数，可以用help interp2 查看函数文档。

3.2.3样条插值

利用函数spline()进行样条插值，函数相关的参数，可以用help spline 查看函数文档。

3.2.4三维插值和高维插值

利用函数interp3()进行三维插值。

利用函数interpn()进行高维插值。

3.3求函数的极限

利用limit()函数求取函数f的极限：

y = limit(f)，求函数f在x=0处的极限
y = limit(f,x,a)或 y = limit(f,a)，求函数f在x=a处的极限
y = limit(f,x,a,'left')，求函数f在x=a处的左极限
y = limit(f,x,a,'right')，求函数f在x=a处的右极限

函数f用符号来定义，比如：

syms x f = sin(x)/x

y = limit(f,x,0)

注意：趋于无穷大时，用inf做参数。

4.积分和微分运算

4.1利用梯形求面积

可以通过函数trapz(x,y)来求定积分。例如：

x = 0:pi/1000:pi

y = sin(x)

trapz(x,y)

4.2单变量积分求解

通过函数quad()进行求解：

quad(Fun,a,b)，对函数Fun在区间[a,b]上求定积分，Fun用函数句柄的方式指定出来。
quad(Fun,a,b,h)，与上面类似，多了一个精度参数h，没有的话默认10^-6
quadl()用法与quad()相同，且精度和速度更高。

4.3双重积分求解

\int_{x m}^{x M} \int_{y m}^{y M} f (x, y) d x d y

通过函数dblquad()进行求解：

dblquad(Fun,xm,xM,ym,yM)，同样Fun通过函数句柄的方式指定出来。
dblquad(Fun,xm,xM,ym,yM,h)，多了一个精度参数。

匿名函数的用法举例：

dblquad(@(x,y) x+y,0,1,0,1)

4.4三重积分求解

\int_{x m}^{x M} \int_{y m}^{y M} \int_{z m}^{z M} f (x, y, z) d x d y d z

通过函数triplequad()进行求解：

triplequad(Fun,xm,xM,ym,yM,zm,zM)，同样Fun通过函数句柄的方式指定出来。
triplequad(Fun,xm,xM,ym,yM,zm,zM,h)，多了一个精度参数。

4.5常微分方程

4.5.1常微分方程的符号解

dsolve()函数来求解常微分方程的符号解，其中Dy表示一阶微分项，D2y表示二阶微分项：

dsolve('equation')，求解常微分方程的通解，默认以t作为自变量。
dsolve('equation','condition')，求解常微分方程的特解。
dsolve('equation1','condition1','equation2','condition2')，求解常微分方程组。
dsolve('equation',x)，求解常微分方程的通解，以x作为自变量。

解常微分方程：

dsolve('Dy-y=sin(x)',x)

dsolve('Dy-y=sin(x)','y(0)=1/2',x)

dsolve('D2y=y','Dy(0) = 3','y(0)=1',x)，求解二阶常微分方程。

解常微分方程组：

z = dsolve('Dx = y','Dy = -x')，再用z.x和z.y来查看求解结果。

4.5.2常微分方程的数值解

数值解一般用的比较少，求常微分方程的数值解可用ode45()，具体参数及用法，用help ode45查看函数文档。

4.6函数的极小值和零点

4.6.1求解一元函数在某个区间上的最小值

x = fminbnd(Fun,a,b)，Fun为函数句柄，a和b为指定区间，返回的x为最小值所对应的自变量的取值。

[x,fval] = fminbnd(Fun,a,b)，返回的x为最小值所对应的自变量的取值，fval为对应的函数值。

fminbnd()函数还可以指定options参数进行优化设置，并且可以显示迭代算法的计算过程，具体操作用help查看。

4.6.2求解多元函数的局部最小值

x = fminsearch(Fun,x0)，其中需要指定一个起始点x0，返回局部最小值对应的自变量取值。

x = fminsearch(Fun,x0,options)，指定options参数进行优化设置。

[x,fval] = fminsearch(Fun,x0)，返回值fval为对应的函数值。

4.6.3求解一元函数的零点

x = fzero(Fun,x0)，指定一个起始点x0，返回零点对应的自变量取值，如果没有找到零点返回NAN。也可以指定一个区间x0，它是一个2维行向量。

x = fzero(Fun,x0,options)，指定options参数进行优化设置。

[x,fval] = fzero(Fun,x0)，返回值fval为对应的函数值。

5.matlab符号计算

5.1符号变量的创建

使用syms命令，后面跟变量名，变量之间用空格隔开。

5.2符号函数和符号方程

符号函数的建立方式：定义好符号变量，直接用一个变量f = 符号变量构成的表达式，这样f就是一个符号函数。

符号方程的建立方式：

利用str2sym()函数，参数是一个字符串，字符串为符号方程的形式。比如：str2sym('x+y==0')
定义一个变量e，把符号变量构成的符号方程表达式赋值给e。比如：e = x+y==0。

一些常用的方法：

求解符号方程的根可以利用solve(e,var)函数，参数e是一个符号方程，参数var指定元。并且solve()函数还可以求解方程组，语法为：z = solve(e1,e2,...x,y,)，通过z.x和z.y来查看方程组的解。
求导数，diff(f)，其中参数f是符号函数。diff(f,x,4)，求f关于x的四阶导数。
求不定积分，int(f,x)函数，其中参数f是符号函数，第二个参数指定对哪个变量求不定积分。
求定积分，int(f,x,a,b)函数，其中参数f是符号函数，第二个参数指定对哪个变量求积分，a和b指定区间。
$\frac{dy}{dt}=ay$ ，用dsolve('Dy = a*y')，进行求解。
limit(f(x),x,0) $limit_{x\to0}f(x)$ 。

5.3符号表达式的基本操作

5.3.1符号表达式的算术运算

加减乘除，与普通变量相同。

5.3.2其他常见的函数

查看一个符号表达式中的符号变量，使用symvar(f)。

factor(f)对符号变量多项式进行因式分解，如果不能分解返回本身。

expand(f)对符号表达式进行展开，可以展开多项式、指数、三角函数等等。

collect(f)对符号表达式中的同类项进行合并。

[a,b] = numden(f)获取符号表达式的分子和分母，a为分子，b为分母。

simplify(f)对符号表达式进行化简。

替换即求值，subs(f(x),x,2)，第一个参数为符号表达式，第二个参数为替换的变量，第三个参数为替换的值，相当于求f(2)。对多个变量进行替换，用subs(f(x,y),{x,y},{3,4})，相当于求f(3,4)。

g = finverse(f)，用于求一个函数的反函数。

compose(f,g)，用于求复合函数，相当于f(g)。

5.4符号矩阵

5.4.1符号矩阵四则运算

符号矩阵中所有的元素都是符号变量，可以进行矩阵的加减乘除四则运算。

5.4.2符号矩阵的其他操作

符号矩阵的转置：A‘是共轭转置，A.’是真正的转置。
符号矩阵的幂运算、秩、求逆、求行列式、求特征值，都与普通矩阵相同。

5.5符号变量与级数

5.5.1级数的求和

利用symsum(f,n,m)函数，进行级数求和。其中f为级数的表达式，n和m表示求第n项到第m项的和。

$\sum_{n=1}^{\infty} \frac{1}{n^2}$ $\frac{\pi^2}{6}$

5.5.2求符号函数的泰勒展开

taylor(f,var)，对符号函数f，求在var=0处的Taylor展开，var指定对哪个变量做展开。比如：taylor(exp(x),x)，求e^x在x=0处的Taylor展开。
taylor(f,var,a)，a参数指定在x = a处展开。

5.6符号函数的积分变换

5.6.1傅里叶变换及其逆变换

傅里叶变换：

F (ω) = \int_{- \infty}^{+ \infty} f (t) e^{- j ω t} d t

f (t) = \frac{1}{2 π} \int_{- \infty}^{+ \infty} F (ω) e^{j ω t} d ω

利用fourier(f)函数进行傅里叶变换，利用ifourier()函数进行傅里叶逆变换。

5.6.2拉普拉斯变换及其逆变换

拉普拉斯变换：

L (s) = \int_{0}^{+ \infty} f (t) e^{- s t} d t

f (t) = \frac{1}{2 π i} \int_{β - i \infty}^{β + i \infty} L (s) e^{s t} d s

利用laplace()函数进行拉普拉斯变换，利用ilaplace()函数进行拉普拉斯逆变换。

5.6.3Z变换及其逆变换

Z变换：

F (z) = \sum_{n = 0}^{\infty} f (n) z^{- n}

f (n) = Z^{- 1} {F (z)}

利用ztrans()函数进行Z变换，利用iztrans()函数进行Z逆变换。

5.7符号函数的图形绘制

采用符号函数来进行图形绘制，图形更为圆滑一些。

5.7.1一元函数图形绘制

fplot()函数：

fplot(f,xinterval)，将在指定区间绘图。将区间指定为[a,b]形式的二元素向量。
fplot(funx,funy,tinterval)，将在指定区间绘图绘制由 x = funx(t) 和 y = funy(t) 定义的曲线，即参数方程定义的曲线。

5.7.2多元函数图形绘制

ezplot()函数：

ezplot(f,[xmin,xmax,ymin,ymax])，其中f(x,y)为包含x和y两个符号变量的表达式，那么将绘制f(x,y)=0的图像，x和y的范围由第二个参数指定。用于绘制二元隐函数图形。
ezplot(funx,funy,[tmin,tmax])，funx、funy都是关于t的函数，用于绘制参数方程定义的曲线。
ezplot3(funx,funy,funz,[tmin,tmax],'animate'))，用于绘制三维空间内由参数方程表示的曲线。animate可以看到动态的绘制过程。

5.7.3极坐标系下图形绘制

ezpolar()函数：

ezpolar(fun(theta))，在极坐标系下进行图形绘制。
ezpolar(fun(theta),[a,b])，[a,b]是theta的范围。

5.7.4绘制三维网格图

ezmesh()函数：ezmesh(f(x,y),domain)，绘制f(x,y) 的曲面，其中domain可以是4×1向量 [xmin, xmax, ymin, ymax] 或2×1向量 [min, max]（其中 min < x < max，min < y < max）。ezmesh(funx,funy,funz,[smin,smax,tmin,tmax])，用于绘制参数方程表示的曲面。

ezmeshc()函数：与ezmesh()函数用法和功能类似，只是在xOy平面多了等高线。

ezcontour()函数：与ezmesh()函数用法类似，专门用来绘制在xOy平面的等高线。

contour()函数：也可用于绘制等高线。通过指定其参数还可以标注等高线的高度。具体用法可以使用help contour来获取文档。例如：创建矩阵 X 和 Y，用于在 xOy平面中定义一个网格。将矩阵 Z 定义为该网格上方的高度。然后绘制 Z 的等高线。

代码如下：

其中meshgrid(x,y)用于生成二维坐标网格，在三维图形绘制中常用。

效果为：

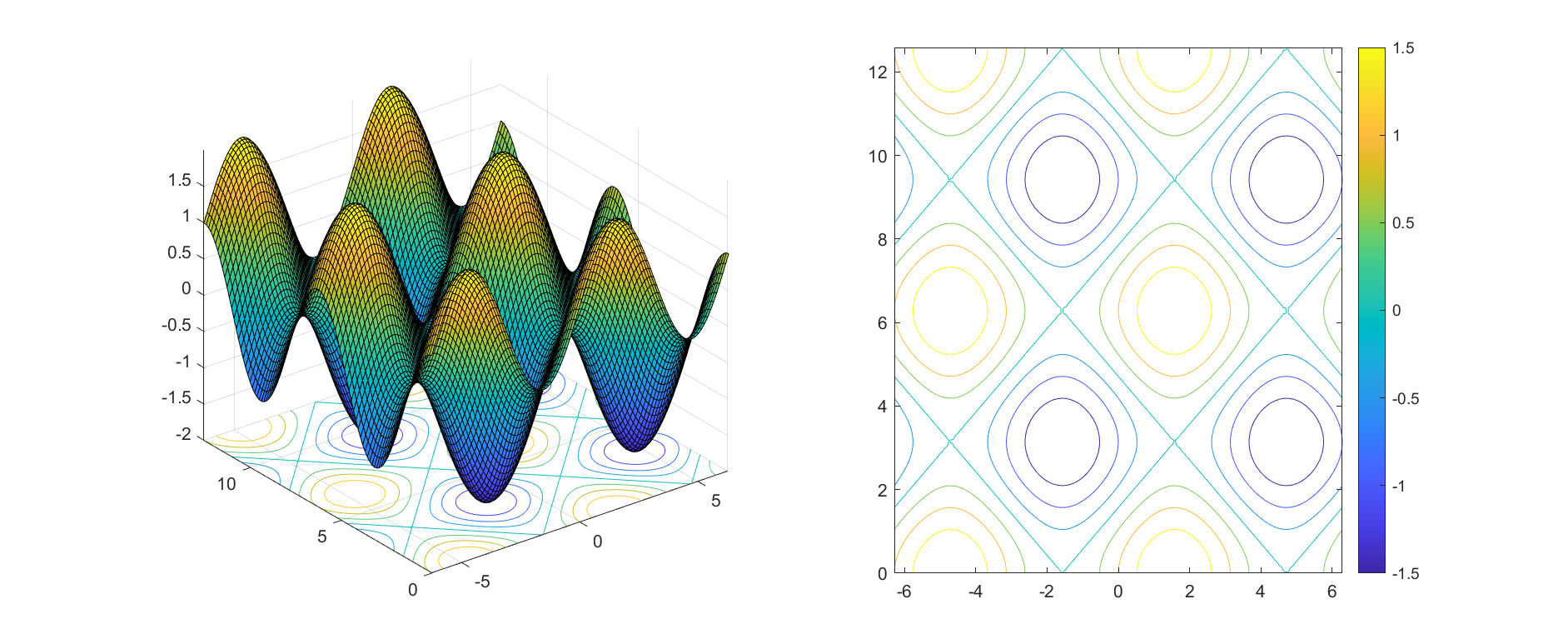
ezcontourf()函数：与ezmesh()函数用法类似，专门用来绘制在xOy平面的等高线（而且与ezcontour()函数相比，图形的颜色被填充）。

ezsurf()函数：与ezmesh()函数功能和用法类似，绘制三维彩色曲面图。

ezsurfc()函数：与ezmesh()函数功能和用法类似，绘制三维彩色曲面图（带有等高线）。

5.8图形化符号函数计数器

5.8.1单变量符号函数计数器

在命令行窗口输入funtool来调用单变量符号函数计数器，操作简单方便。

5.8.2泰勒级数逼近计数器

在命令行窗口输入taylortool来调用泰勒级数逼近计数器，操作简单方便。

6.二维数据可视化

6.1基本绘图函数plot()

6.1.1plot()函数

只有一个参数，plot(y)：

如果y是一个向量，默认横坐标为1、2、3...，y作为纵坐标向量进行绘图。
如果y是一个矩阵，则对每一列进行绘图。
如果y是一个复数组成的向量，以实部为x轴、虚部为y轴进行绘图。

两个参数，plot(x,y)：

如果x和y都为向量，则以x为横坐标，y为纵坐标进行绘图。
如果x是向量，y为矩阵，则以x为横坐标，y的每一列为纵坐标绘制多条曲线。
如果x和y都为矩阵，它们必须是相同的规格，以x的第i列为横坐标，y的第i列为纵坐标进行多条曲线的绘制。

三个参数，plot(x,y,s)：

多了一个s参数，它是一个字符串，用于控制线的颜色、类型、点的形状等等。比如：s = 'r-.*'表示红色的点划线，且点的形状为星号。其他的样式类型在需要的时候，通过help plot命令查看函数文档。

多个参数，plot(x1,y1,s1,x2,y2,s2...)：

同时在一个坐标系内绘制多条曲线，且可指定每一条线的样式。

6.1.2子图的绘制subplot()函数

subplot(m,n,p)：

该函数将当前的图形窗口分为m×n（m行n列）个绘图区，子图区的编号按照行优先的顺序进行。
p参数指定在第p个子图上进行绘制。
每一个子图区允许以不同坐标系进行绘图。

6.1.3叠加图的绘制

需要在已经绘制好的图形上添加新的图形，使用hold命令：

hold on，打开叠加绘图
hold off，关闭叠加绘图
hold，在打开和关闭之间切换。

6.1.4坐标轴的设置

使用axis()函数：

axis([xmin,xmax,ymin,ymax])，定义x和y轴的范围。
axis([xmin,xmax,ymin,ymax,zmin,zmax])，定义三维坐标系的坐标轴范围。
axis equal命令，x轴和y轴等刻度。
axis square命令，使用正方形坐标系。
axis auto命令，使坐标轴范围容纳所有图形。

其他命令通过help来获取。

6.1.5网格线的设置

使用grid命令：

grid on，显示网格线。
grid off，关闭网格线。
grid，在打开和关闭之间切换。

6.1.6图形的缩放

图形的缩放可以只沿x轴方向，这个功能有时候可能有用。使用zoom命令，有需要的时候可以使用help zoom进行查看。

6.1.7极坐标下进行绘图

使用函数polar()：

polar(theta,rho)，其中theta为极角，rho为极径。
polar(theta,rho,s)，s参数可设置线型。

拓展：在matlab中极坐标和直角坐标下的坐标可以相互转换。pol2cart()将极坐标转换为直角坐标，cart2pol()将直角坐标转换为极坐标。

6.1.8对数和半对数坐标系绘图

semilogx(x,y)，x轴采取对数坐标，y轴为等比例坐标。
semilogy(x,y)，y轴采取对数坐标，x轴为等比例坐标。
loglog(x,y)，x轴和y轴都是对数坐标。

6.1.9双y轴图形绘制

有时候想把两个曲线显示在同一个坐标系内，但是由于单位长度的问题导致如果显示了其中一个就看不到另一个的变化趋势了，比如：同时绘制指数函数和正弦函数。这时就要采用双y轴来进行绘制了。使用函数plotyy()。

比如：plotyy(x,y,x,z,'plot','semilogy')，表示采用双y轴，且x和y向量采用等比例坐标系，x和z向量采用对数坐标系。

6.2图形的窗口和标注

6.2.1图形的窗口

在figure窗口下的工具栏可以实现添加文字、添加箭头、设置线型等等很多操作，操作比较简单，不多赘述。

6.2.2图形的标注

添加图形的标题：title('string')函数来进行标题设置。

坐标轴标签：xlabel('string')、ylabel('string')，分别对x轴和y轴添加标签。

添加图例：legend('s1','s2','s3'...)，按照绘图的顺序，给出各个曲线的文字描述。

显示颜色条：常用于三维绘图和二维等高线绘图中，通过命令colorbar来进行添加。

添加文本框：文本用于对图形的说明，一般通过figure窗口来进行操作，因为比代码方便。

6.3特殊图形的绘制

特殊图形绘制，包括柱状图、饼状图、直方图、散点图等等。

6.3.1柱状图

利用bar()函数：

bar(y)，默认x下标为1、2、3...
bar(x,y)，x为下标，y为柱的高度，绘制柱状图。
还可添加width、color等设置，通过help bar查看。

还可以绘制水平方向的柱状图，使用函数barh()，用法与bar()函数相同。

6.3.2饼状图

利用pie()函数：

pie(x)，以x向量绘制饼状图，如果x向量元素和大于1，则自动进行归一化。如果小于1，得到不完整的饼（有时候也是一种需要）。
pie(x,explode)，explode参数与x维数相同，explode不为0的位置，饼状图会凸显。
pie(x,labels)，labels用于指定饼状图标签。

6.3.3直方图

利用hist()函数：

hist(y)，将向量y中的元素放入10个柱的直方图中。
hist(y,m)，m指定柱的个数，将向量y中的元素放入m个柱的直方图中。
hist(y,x)，x为向量，将参数y中的元素放到 length(x) 个由x中元素指定的位置为中心的直方图。

6.3.4散点图

利用scatter()函数：

scatter(x,y)，以x为横坐标、y为纵坐标绘制散点图。
scatter(x,y,sz,c)，sz指定散点大小，c指定散点颜色。

6.4工科数学中常见的一些图形绘制

6.4.1火柴杆图

火柴杆图常用于信号与系统中离散序列的绘制，使用stem()函数：

stem(y)，默认x = 1、2、3...
stem(x,y)，以x为横坐标、y为纵坐标绘制。

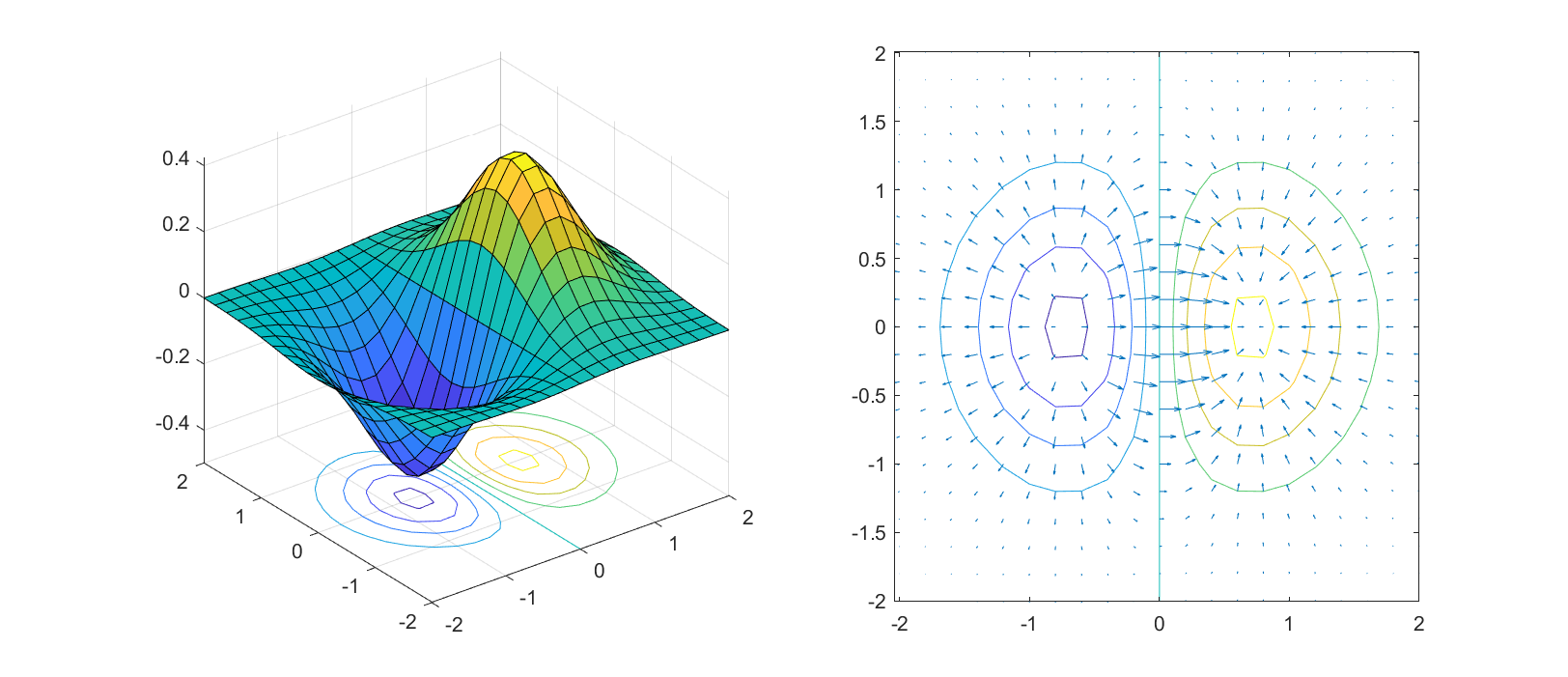
6.4.2向量场图

向量场图使用quiver()函数进行绘制：

quiver(X,Y,u,v)用于绘制向量场图，X、Y为[X,Y] = meshgrid(x,y)网格化后的两个矩阵，u、v为对应位置的向量场分量。

$xe^{-x^2-y^2}$ 在网格上的二维梯度。

效果如下：

7.三维数据可视化

7.1plot3()绘制三维曲线图

函数plot3()用法如下：

plot3(x,y,z)，x、y、z是相同维度的向量，绘制一条三维曲线。
plot3(X,Y,Z)，绘制多条三维曲线，X、Y、Z第i列对应第i条曲线。

7.2mesh()绘制三维网格图、surf()绘制三维曲面图

三维网格图：

常用两个函数：

[X,Y] = meshgrid(x,y)产生平面区域内的网格坐标矩阵。
mesh(X,Y,Z)来绘制三维网格图。

另外，使用meshc()可以绘制带等高线的三维网格图、meshz()绘制带有底座的三维网格图。用法与mesh()类似。

三维曲面图：

函数surf()绘制三维曲面图：

[X,Y] = meshgrid(x,y)产生平面区域内的网格坐标矩阵。
surf(X,Y,Z)来绘制三维曲面图。

另外，使用surfc()可以绘制带等高线的三维曲面图。

7.3特殊三维绘图

7.3.1柱面图

经常用于绘制旋转体，使用函数cylinder()生成坐标：

[X,Y,Z] = cylinder(r,n)，基于向量 r 定义的剖面曲线返回圆柱的 X、Y 和 Z坐标。该圆柱绕其周长有n个等距点。
n代表了柱面的精细程度，n越大柱面越光滑精细。
利用生成的坐标绘制三维曲面图会发现柱面的高度为1，如果实际是以r的参数范围为高度，需要对Z坐标进行放缩。

7.3.2球面图

使用函数sphere()来生成球面坐标：

[X,Y,Z] = sphere(n)，n代表精细程度，n越大球面越光滑。
生成的坐标为单位球面的坐标，如果要绘制半径为10的球面，要将对应的X、Y、Z坐标乘以10。

7.3.3三维等高线

使用函数contour3()来绘制三维等高线：

contour3(X,Y,Z)，与前面mesh()用法类似。
还可以指定levels参数来给出层级，levels越大，等高线的梯度越小。具体其他用法，使用help contour3查看函数文档。

7.3.4三维柱状图

使用函数bar3()：

bar3(Z)，Z为一个m行n列的矩阵，绘制的时候会以Z的每一行为单位进行，对应的index为1、2、3...n，一共绘制m个行。
bar3(Y,Z)，指定Y参数，其中Y参数是一个m维的向量，用于给每一行定制序号。

使用函数bar3h()绘制水平方向上的三维柱状图。

7.3.5三维饼状图

使用函数pie3()：

使用方法与二维函数pie()相同，都是传一个x向量，用explode参数指出突出显示的部分。

7.3.6三维散点图

使用函数scatter3()：

scatter3(x,y,z)，x、y、z为三个维度相同的向量，会以(x(i),y(i),z(i))为第i个散点的坐标，一共绘制length(x)个散点。

7.3.7三维火柴杆图

使用函数stem3()：

stem3(x,y,z)，与scatter3()函数用法一样，只不过在散点的基础上增加了火柴杆。

7.3.8三维向量场图

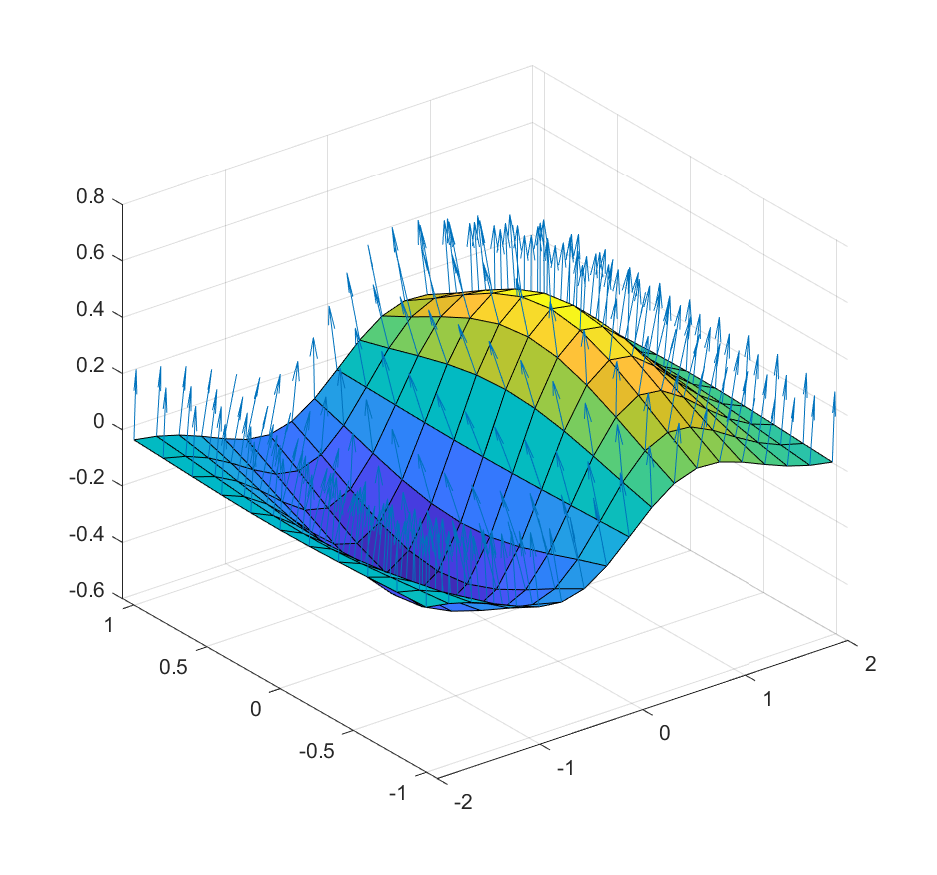
使用函数quiver3()：

quiver3(X,Y,Z,U,V,W)，在 (X,Y,Z) 确定的点处绘制向量，其方向由分量 (U,V,W) 确定。矩阵 X、Y、Z、U、V 和 W必须是相同规格。
经常配合[U,V,W] = surfnorm(X,Y,Z)来绘制曲面的法向量图。

$z=xe^{-x^2-y^2}$ 的曲面法线图

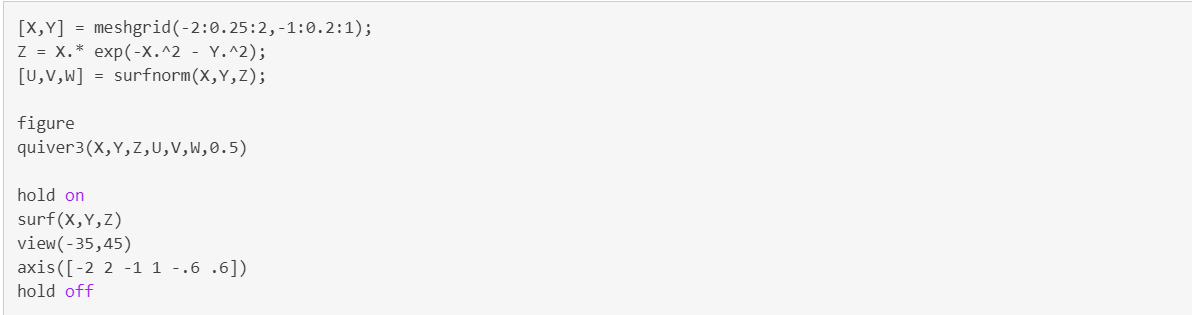
效果如下：

7.4三维绘图中的其他设置

7.4.1设置视角

建议在figure窗口下，用鼠标拖动来设置视角，不建议用代码操作，代码太麻烦而且机械。

7.4.2使用hidden

利用函数mesh()绘制三维网格图时，默认隐藏三维图形中被遮挡的部分，可以使用hidden off命令来透视看到被隐藏的部分，效果如下：

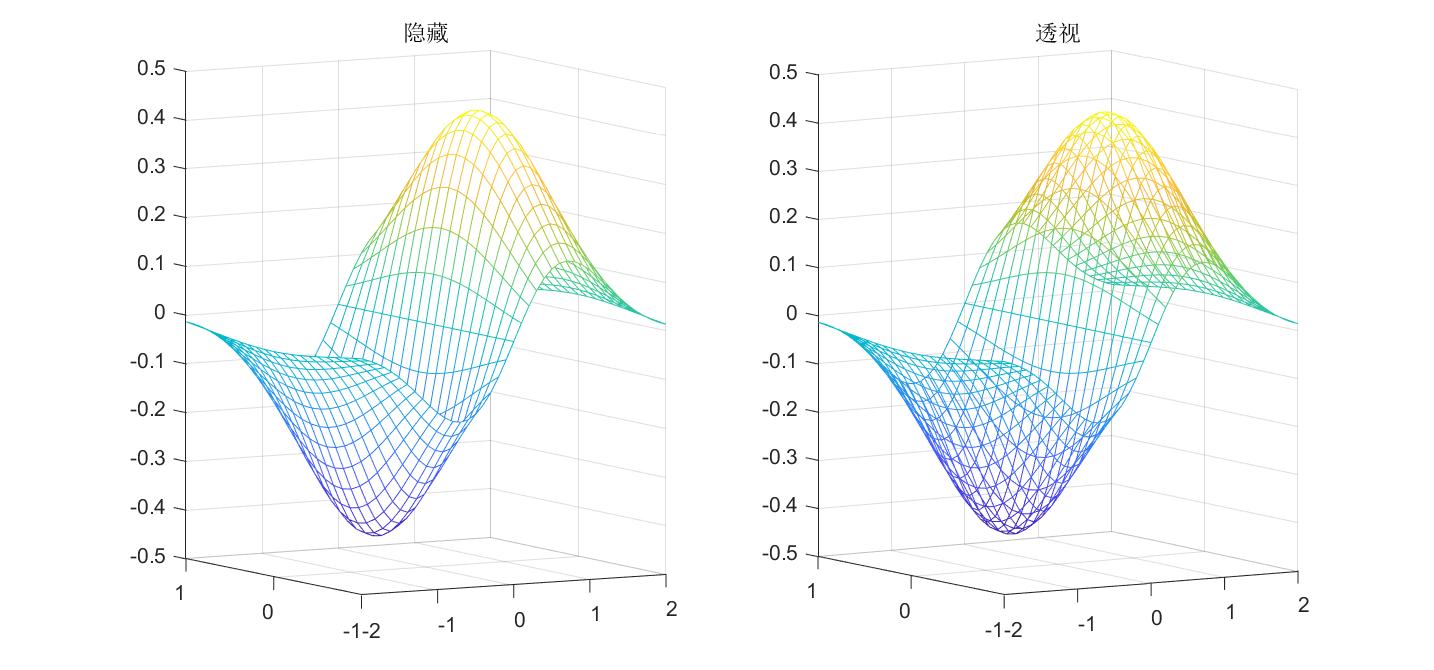
7.4.3设置颜色

使用colormap命令，具体颜色类型可以使用help colormap查看文档。

8.matlab基本编程

8.1m文件的类型

在matlab中，m文件有两种类型，脚本和函数，都是以.m作为后缀名。m文件为普通ASCLL文件，可以采用文本编辑器来编辑。

8.1.1脚本m文件

脚本文件中的变量都为全局变量，这些变量保存在matlab基本工作区中。为了避免变量名相同引起冲突，一般在脚本文件的开始使用clear all命令。

8.1.2函数m文件

函数m文件在执行的过程中，所产生的变量一般都是局部变量，存放在函数自身的函数工作区中，不会和基本工作区里面的变量产生冲突。对于用户来说函数m文件就像一个黑匣子，只有输入和输出。注意：函数m文件的第一行，需要用function关键字来声明这个文件是函数m文件，且函数名必须与文件名相同。

声明形式为：function 输出参数 = 函数名(输入参数)

函数采用的参数传递方式为值传递，将变量或常量的值传递给函数形式参数指定的变量，函数在经过计算后，将返回值传递回基本工作区，函数工作区中的变量被清除。

在matlab中，nargin的值为输入参数的个数，nargout的值为输出参数的个数。可以用if-else语句配合这两个参数，实现不同输入参数、不同输出参数函数行为不同的效果。

8.2程序结构

8.2.1顺序结构

最为常用，程序从上到下依次执行每条语句。

8.2.2分支结构

if-end语句，示例如下：


1
if a >= b
2
    a = b;
3
end

if-else-end语句，示例如下：


xxxxxxxxxx
6
1
%rem(a,b)函数为求余运算
2
if rem(a,2)==0
3
    disp('偶数');
4
else
5
    disp('奇数');
6
end

if-elseif-else-end语句，示例如下：


xxxxxxxxxx
9
1
x = 94;
2
if x>90
3
    disp('优秀');
4
elseif x>80
5
    disp('良好');
6
elseif x>60
7
    disp('及格');
8
else
9
    disp('不及格');

switch-end语句，示例如下：


xxxxxxxxxx
10
1
switch x
2
    case 1
3
        disp('x=1');
4
    case 2
5
        disp('x=2');
6
    case {3,4,5}
7
        disp('x=3,4,5');
8
    otherwise
9
        disp('x为非1到5的数字');
10
end

8.2.3循环结构

for循环语句：


x
1
%使用for循环
2
for i = 1:10
3
    x(i) = i^2;
4
end
5

6
%使用向量、矩阵运算
7
j = 1:10;
8
y = j.^2;

比较推荐用向量和矩阵运算来代替循环，因为这样计算效率比较高。

另外，循环还支持嵌套，例如：


xxxxxxxxxx
6
1
x = zeros(5,5);
2
for i = 1:5
3
    for j = [1,2,3,4,5]
4
        x(i,j) = i*j;
5
    end
6
end

while循环语句：


xxxxxxxxxx
7
1
x = 1:10;
2
i = 1;
3
sum = 0;
4
while i<=length(x)
5
    sum = sum+i;
6
    i = i+1;
7
end

此外，matlab中也有break语句和continue语句，与C中用法相同，break用于退出一层循环，continue用于退出本次循环。

8.3函数

8.3.1主函数

在每个函数m文件的第一行定义的函数就是主函数。一个函数m文件只有一个主函数，其函数名与文件名相同。

8.3.2子函数

在同一个函数m文件下，主函数后面可以定义一些子函数，当主函数里面用到子函数时，可以对其进行调用。当外部的一些主函数与内部定义的子函数重名时，优先使用内部定义的子函数，这个现象也叫做函数的重载。另外注意：子函数只能被在同一个m文件下的主函数或其他子函数调用。

示例如下：


xxxxxxxxxx
12
1
function y = mymaxmain(x1,x2)
2
%主函数
3
%输入x1和x2均为向量
4
%返回y为标量
5
y1 = mymax(x1);
6
y2 = mymax(x2);
7
y = max(y1,y2);
8
end
9

10
function z = mymax(x)
11
z = max(x);
12
end

8.3.3匿名函数

匿名函数定义的语法格式为：f = @(参数列表) 返回的表达式。

匿名函数可以返回多个值，示例如下：


xxxxxxxxxx
3
1
f = @(x) [max(x),min(x)];
2
x = [1,3,5,7,9];
3
f(x)

多重匿名函数，示例如下：


xxxxxxxxxx
3
1
f = @(a,b,c)@(x) a*x^2+b*x+c;
2
f1 = f(1,2,3);          %f1仍为一个匿名函数，相当于f1 = @(x) x^2+2*x+3
3
f1(3)

8.3.4函数句柄

函数句柄简单理解就是一个名字，示例如下：


xxxxxxxxxx
2
1
f = @cos;
2
f(3.1415)

函数句柄有许多好处，最常用的好处就是可以配合匿名函数实现一个函数的快速定义。

8.4人机交互命令

8.4.1keyboard

在脚本执行的过程中，常用keyboard对程序进行调试。在代码运行的时候遇到keyboard，程序会进入命令行模式，此时用户可以对变量的值进行查看或修改，待点击继续后，代码恢复继续向下执行。它的相当于一个断点。例如：


xxxxxxxxxx
4
1
a = [1,2,3;4,5,6];
2
b = [2,4,6;8,10,12];
3
keyboard;
4
a+b

8.4.2pause

程序运行到pause语句会停止，当按任意键后，程序继续向后执行。常用于动态的画图演示。示例如下：


xxxxxxxxxx
10
1
x = 0:0.1:2*pi;
2
y = sin(x);
3
figure;
4
plot(x,y);
5
hold on;
6
for i=1:6
7
    pause;
8
    plot(x,sin(x+i/5));
9
    hold on;
10
end

9.概率与数理统计

9.1随机数的产生

9.1.1二项分布随机数

使用函数binornd()产生二项分布随机数。

r = binornd(n,p)，产生一个随机数。
r = binornd(n,p,m,n)，产生m行n列的随机数矩阵。

9.1.2泊松分布随机数

使用函数poissrnd()产生泊松分布随机数。

poissrnd(lambda) $\lambda$ 为泊松分布的参数。
poissrnd(lambda,m,n)，产生m行n列的随机数矩阵。

9.1.3指数分布随机数

使用函数exprnd()产生指数分布随机数。

exprnd(lambda) $\lambda$ 为指数分布的参数。
exprnd(lambda,m,n)，产生m行n列的随机数矩阵。

9.1.4均匀分布随机数

unifrnd()产生连续型均匀分布随机数。

unifrnd(a,b)，产生区间[a,b]上的均匀分布。
unifrnd(a,b,m,n)，产生m行n列的随机数矩阵。

unidrnd()产生离散型均匀分布随机数。

unidrnd(N)，产生从1到N之间的离散均匀随机整数。
unidrnd(N,m,n)，产生m行n列的随机数矩阵。

9.1.5正态分布随机数

使用函数normrnd()产生正态分布随机数。

normrnd(mu,sigma) $\mu$ $\sigma$ 的正态分布随机数。
normrnd(mu,sigma,m,n)，产生m行n列的随机数矩阵。

9.2概率密度函数

9.2.1常见离散型分布的概率密度函数

使用函数y = binopdf(x,n,p)产生二项分布概率密度函数。其中x=[0:1:n]，得到p向量的第i个元素就是p(n=i-1)的概率。然后用plot(x,p)就能绘制出概率密度函数图。

使用函数y = poisspdf(x,lambda)产生泊松分布概率密度函数。用法与上面二项分布相同。

使用函数y = geopdf(x,p)产生参数为p的几何分布概率密度函数。

使用函数y = unidpdf(x,N)产生离散型均匀分布的概率密度函数。

9.2.2常见连续型分布的概率密度函数

使用函数y = unifpdf(x,a,b)产生[a,b]上均匀分布的概率密度函数。

y = exppdf(x,lambda) $\lambda$ 的指数分布的概率密度函数。

y = normpdf(x,mu,sigma) $\mu$ $\sigma$ 的正态分布的概率密度函数。

9.2.3三大抽样分布的概率密度函数

使用函数y = chi2pdf(x,nu)，产生卡方分布的概率密度函数。

使用函数y = tpdf(x,nu)，产生t分布的概率密度函数。

使用函数Y = fpdf(X,V1,V2)，产生F分布的概率密度函数。

9.3随机变量的数字特征

9.3.1样本平均值和中位数

y = mean(x)，对向量x中的元素求算术平均值。如果x为一个m×n的矩阵，对矩阵的每一列求平均值，返回1×n的向量。y = mean(x,2)对矩阵的每一行求平均值，返回m×1的向量。

y = nanmean(x)，忽略NAN求算术平均值。其他用法与mean()函数相同。

y = geomean(x)，计算几何平均数。

y = harmmean(x)，计算调和平均数。

几何平均数：

y = \sqrt[n]{x_{1} x_{2} . . . x_{n}} = \sqrt[n]{\prod_{i = 1}^{n} x_{i}}

调和平均数：

y = \frac{1}{\frac{1}{n} \sum_{i = 1}^{n} \frac{1}{x_{i}}} = \frac{n}{\sum_{i = 1}^{n} \frac{1}{x_{i}}}

y = median(x)，计算中位数。

y = nanmedian(x)，忽略NAN计算中位数。

9.3.2样本数据的排序

y = sort(x)，对向量x的元素进行从小到大排序。如果x是一个矩阵，默认按列进行排序，y = sort(x,2)按行进行排序。指定descend从大到小排序。

y = range(x)，求向量最大值与最小值之差。如果是矩阵默认按列进行，y = range(x,2)按行进行。

y = minmax(x)，求向量的最小值和最大值。如果是矩阵，只能按照行进行操作。不支持2个参数。

9.3.3样本期望和方差

y = mean(x)，计算样本数据的期望。如果x是矩阵，则按列进行操作。

y = var(x)，计算样本数据的方差。

y = std(x)，计算样本数据的标准差。

注意样本数据的方差为：

s = \frac{1}{n - 1} \sum_{i = 1}^{n} (s_{i} - \bar{s})

9.3.4常见分布的期望和方差

[E,Var] = binostat(n,p)，计算二项分布的期望和方差。

[E,Var] = unifstat(a,b)，计算[a,b]上均匀分布的期望和方差。

[E,Var] = normstat(mu,sigma)，计算正态分布的期望和方差。不过正态分布的期望与方差根据参数显然能看出来，一般不用这个函数求。

[E,Var] = expstat(lambda)，计算指数分布的期望和方差。

[E,Var] = tstat(nu)，计算t分布的期望和方差。

[E,Var] = fstat(V1,V2)，计算F分布的期望和方差。

9.3.5协方差与相关系数

样本协方差：

S_{X Y} = \frac{\sum_{i = 1}^{n} (X_{i} - \bar{X}) (Y_{i} - \bar{Y})}{n - 1}

使用函数S =cov(X,Y)，其中X、Y为相同维度（都是向量）的样本数据，返回S为一个协方差矩阵。

\begin{matrix} S = [\begin{matrix} c o v (X, X) & c o v (X, Y) \\ c o v (Y, X) & c o v (Y, Y) \end{matrix}] \end{matrix}

如果参数只有一个矩阵X，S = cov(X)，则以列为单位求取协方差矩阵，下面的X(i)代表X的第i列。即

\begin{matrix} S = [\begin{matrix} c o v (X (1), X (1)) & c o v (X (1), X (2)) & . . . & c o v (X (1), X (n)) \\ c o v (X (2), X (1)) & c o v (X (2), X (2)) & . . . & c o v (X (2), X (n)) \\ . . . & . . . & . . . & . . . \\ c o v (X (n), X (1)) & c o v (X (n), X (2)) & . . . & c o v (X (n), X (n)) \end{matrix}] \end{matrix}

9.4统计图的绘制

前面介绍过柱状图、饼图、直方图等统计图的绘制，这里做一些其他的补充。

9.4.1正整数频率表

使用函数T = tabulate(X)，X为一个正整数向量，返回值包含3列，第1列为正整数值，第2列为出现次数，第3列为频率。

9.4.2带有正态密度曲线的直方图

使用函数histfit(data,n)，其中data为样本数据构成的向量，n为直方图的组数。

9.4.3正态分布的概率密度曲线

normspec([a,b],mu,sigma) $\mu$ $\sigma$ 的正态分布概率密度曲线，并指出在[a,b]上的概率。