Problem
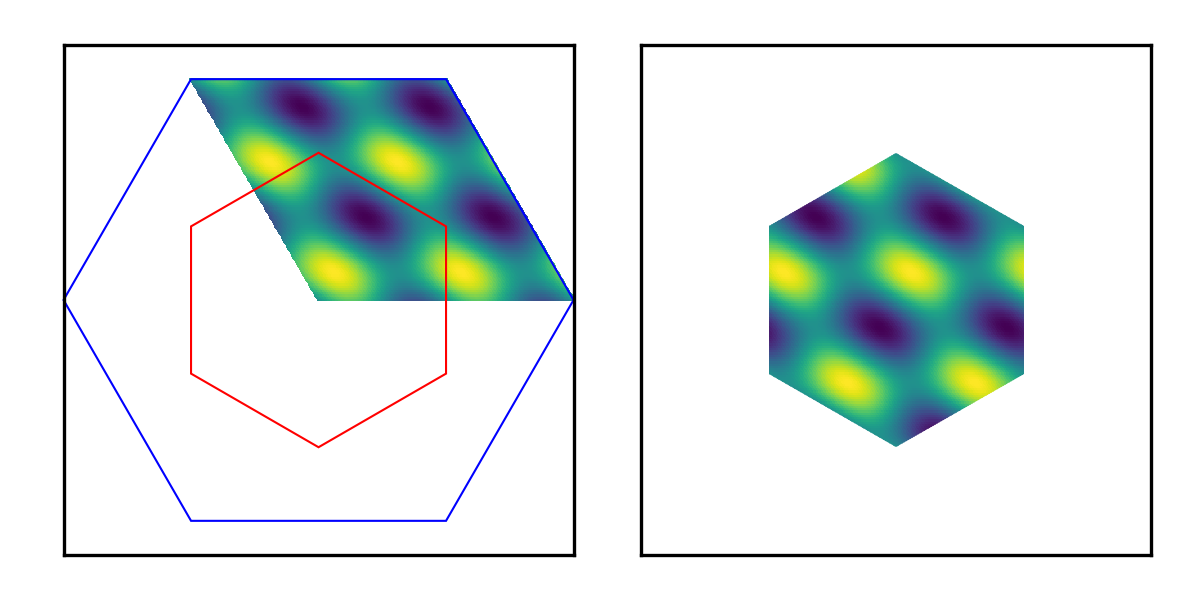
Suppose we have a periodic function $f(x,y)$ defined within a hexagonal unit cell, how can we plot the function on the Wigner-Seitz cell?
Codes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from matplotlib.patches import Polygon
# lattice constant of th 2D honeycomb cell
L = 1.0
# number of grid points in each direction
nx, ny = 100, 100
# The 2D cell basis vector
cell = L * np.array([[1.0, 0.0], [-0.5, np.sqrt(3) / 2.]])
# the fractional coordinates of the grid points
x0, y0 = np.mgrid[0:1:1j*nx, 0:1:1j*ny]
# the Cartesian coordinates of the grid points
x1, y1 = np.tensordot(cell, [x0, y0], axes=(0, 0))
# any periodic functions
w = 2
z = np.sin(w * 2 * np.pi / L * x0) + np.sin(w * 2 * np.pi / L * y0)
fig = plt.figure(
figsize=(4.0, 2.0),
dpi=300
)
axes = [plt.subplot(121), plt.subplot(122)]
############################################################
ax = axes[0]
ax.pcolormesh(x1, y1, z, shading='auto')
cc = L * np.exp(1j * np.pi / 3 * np.arange(7))
hh = Polygon(np.c_[cc.real, cc.imag],
lw=0.5, edgecolor='b',
clip_on=False, facecolor='none')
ax.add_patch(hh)
cc = L * np.sqrt(3) / 3 * np.exp(1j * np.pi * (1./6 + 1./3 * np.arange(7)))
hh = Polygon(np.c_[cc.real, cc.imag],
lw=0.5, edgecolor='r',
clip_on=False, facecolor='none')
ax.add_patch(hh)
############################################################
ax = axes[1]
cc = L * np.sqrt(3) / 3 * np.exp(1j * np.pi * (1./6 + 1./3 * np.arange(7)))
hh = Polygon(np.c_[cc.real, cc.imag],
lw=0.0, edgecolor='k',
clip_on=False, facecolor='none')
ax.add_patch(hh)
for ii in range(-1, 1):
for jj in range(-1, 1):
x2, y2 = np.tensordot(cell, [x0 + ii, y0 + jj], axes=(0, 0))
img = ax.pcolormesh(x2, y2, z, shading='auto')
img.set_clip_path(hh)
for ax in axes:
ax.set_aspect(1.0)
ax.set_xlim(-L, L)
ax.set_ylim(-L, L)
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
plt.savefig('kaka.png')
# plt.show()
The results
Right panel: The same periodic function on the Wigner-Seitz cell.