Ratio of Potential and Kinetic Energy
The dimensionless ratio of the potential energy ($U$) and the kinetic energy $K$, known as $\gamma_s$, can be written as 1
\[\begin{align} \gamma_s &= \frac{U}{K} = \frac{g}{a_0} \, \frac{m^{\ast}}{\epsilon} \, \frac{1}{\sqrt{\pi n_e}} \\[9pt] &= \frac{g}{a_0} \, \frac{m^{\ast}}{\epsilon} \, \frac{\lambda_m}{\sqrt{2\pi\nu/\sqrt{3}}} \\ \end{align}\]where
-
$g=2$ is the valley degeneracy factor,
-
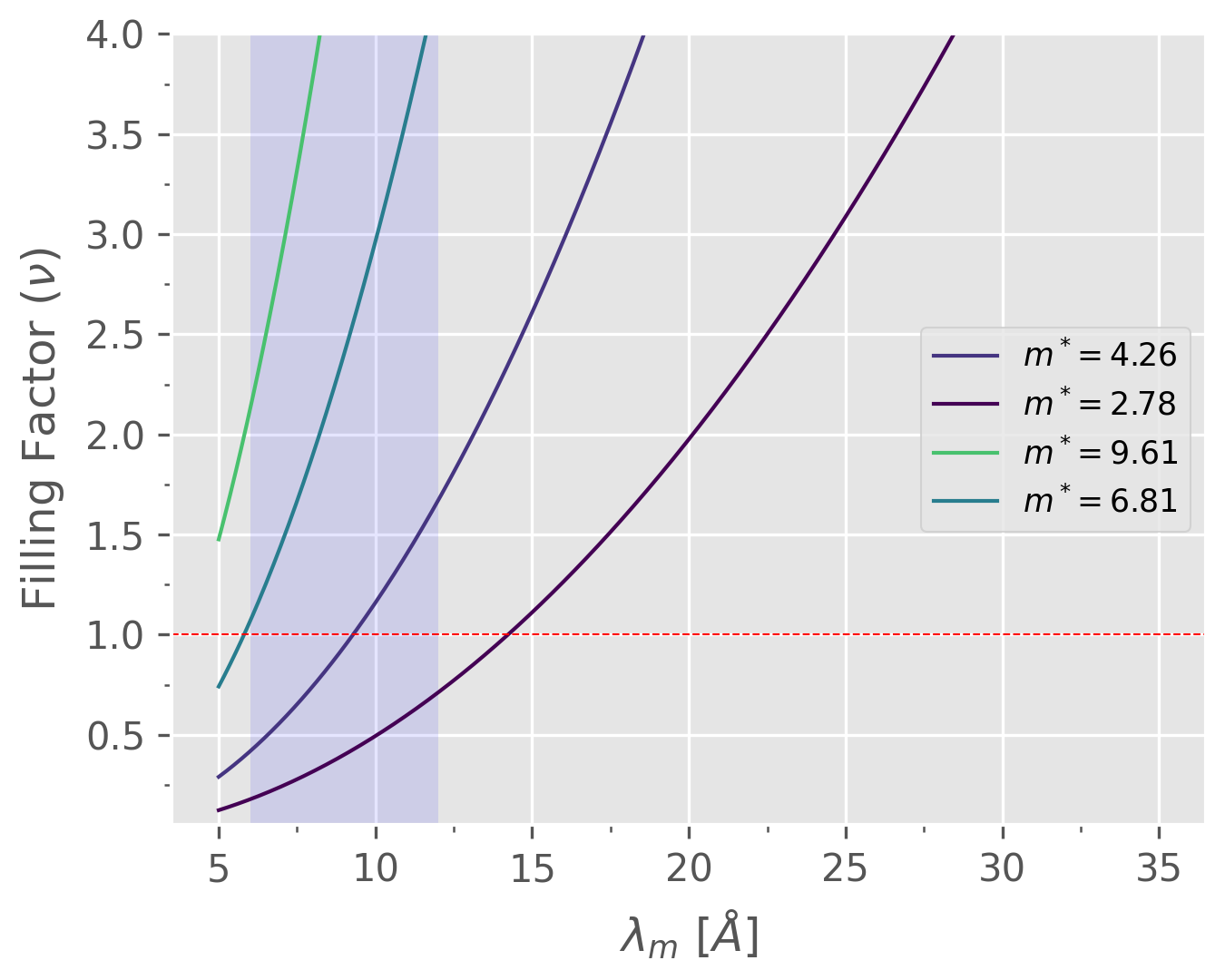
$m^\ast$ is the effect carrier mass in unit of electron mass $m_0$. From DFT calculations of 1ML CoCl2 (by Mr. Aolei Wang), one can get the effective carrier mass at different band extrema.
- VBM($\Gamma – M$): $m^\ast = 4.26$
- VBM($\Gamma – K$): $m^\ast = 2.78$
- CBM($K – \Gamma$): $m^\ast = 9.61$
- CBM($K – M$): $m^\ast = 6.81$
-
$a_0 = \hbar^2 / m_0 e^2 = 0.529\,\mathring{A}$ is the Bohr radius,
-
$\epsilon$ is the effective dielectric constant. By treating the bilayer as two dielectrics in series,
\[\begin{equation} \frac{d_1 + d_2}{\epsilon} = \frac{d_1}{\epsilon_1} + \frac{d_2}{\epsilon_2} \end{equation}\]where $\epsilon_i$ and $d_i$ are the dielectric constants and the thickness of the top and bottom layers, respectively. For CoCl2/HOPG bilayer, we choose
-
$\lambda_m$ is the lattice parameter of the moiré lattice. If two hexagonal sublattices with lattice constants $a_1$ and $a_2$ ($a_2 > a_1$) rotate by an angle $\theta$, then the moiré periodicity is given by 4
\[\begin{equation} \lambda_m \approx \frac{a_2}{\sqrt{\delta^2 + 4\sin^2(\theta / 2)}}, \qquad \delta = 1 - \frac{a_1}{a_2} \end{equation}\]For CoCl2/HOPG
-
$a_{\mathrm{CoCl}_2} = 3.528\,\mathring{A}$ from Ref 5
-
$a_\mathrm{HOPG} = 2.468\,\mathring{A}$ from Ref 6
There is a large lattice mismatch and the moiré periodicity can not be estimated from the above equation. Experimentally, $\lambda_m$ for CoCl2/HOPG falls within $[6, 12]\,\mathring{A}$.
-
-
$\nu$ is the filling factor,
-
$n_e$ is the charge density,
\[\begin{equation} n_e = \frac{\nu}{\sqrt{3}\lambda_m^2/2} \end{equation}\] -
critical value for GWCs is $\gamma_s = 29.5$.
Mott criterion
Mott states and Wigner crystal are both due to the strong Coulomb repulsion between electrons, with the former dominated by intrasite and the latter intersite interaction. Moreover, the Mott states must satisfy the Mott criterion. [1,7]
\[\begin{equation} \sqrt{n_e}\,a_0^\ast \approx 1 \end{equation}\]where
-
$a_0^\ast$ is the effective Bohr radius
\[\begin{equation} a_0^\ast = \frac{\hbar^2\epsilon}{m^\ast m_0\,e^2} = \frac{\epsilon}{m^\ast}\,a_0 \end{equation}\]
$\gamma_s$ as function of charge density
- As can be seen from the above figure, for $\lambda_m$ in the range of $[6, 12]\,\mathring{A}$ and filling factor $\nu = 1$, $\gamma_s$ is far below the critical value of 29.5, which indicates it is not possible to Wigner crystalize in CoCl2/HOPG based on this simple model.
- Clearly, with much larger effective mass, the possibility to Wigner crystalization increases.