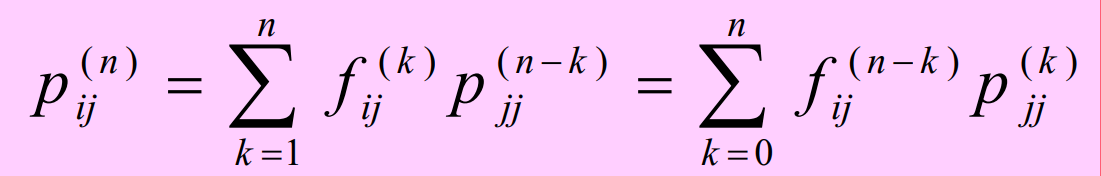Stochastic Process
HW6
如有错误,烦请指正.
1
判断二维对称随机游动的常返性.
状态 常返的充分必要条件是
所以只需要判断这个级数的敛散性即可.
因为
而与一维随机游动同理,从原点(状态 )出发只有转移偶数步才能回到原点,所以
所以
考虑 . 设这 步中,有 步是在 方向移动,有 步是在 方向移动,则
对给定的 ,求这种分法的种类数. 这相当于古典概型中的不尽相异元素的排列,即 个元素属于 个不同的类,各类元素分别有 个,,则把它们排成一列共有
种排法,而 个元素分为 类总共有 种分法,所以
证明
考虑恒等式
左边展开,
右边展开,
比较两边系数就有
特别,
下面对这个结果进行估计. 根据 Stirling 公式,
所以
也就是说状态 是常返的,进而二维对称随机游动是常返的.
特别,这个过程还是零常返的,这是因为 ,
当 时,
当 时,
所以,
即这个过程是零常返的.
2
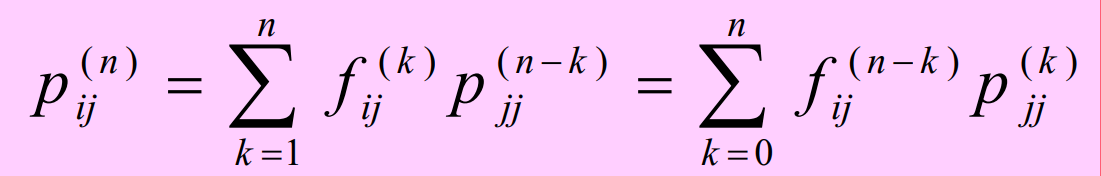
证明:
首先证明
观察到
设事件
这里 .
于是
所以
再证明
注意到
设事件
这里 .
于是
与前面类似,有
3

因为
所以状态 是常返的.
又因为
所以状态 是正常返的.
因为
所以
即状态 是瞬过的(非常返的).
因为
所以状态 是常返的.
又因为
所以状态 是正常返的.
易知
猜想
其中 . 用归纳法证明.
所以
其中
所求极限为
注意到 ,所以这个极限也可以表示为