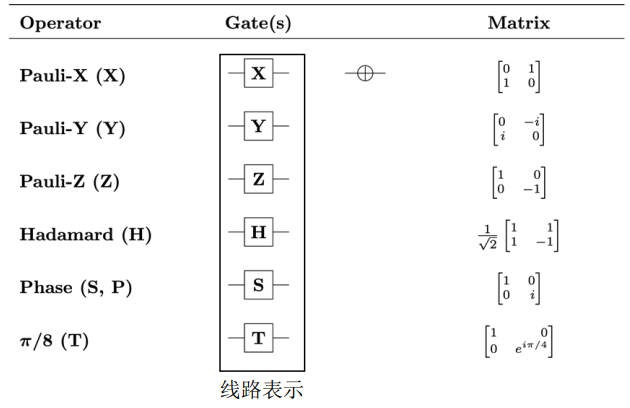
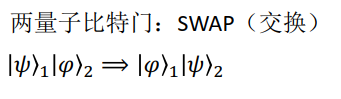量子物理
第一章 光的特性
1.2 几何光学与费马原理
1.2.1. 几何光学的基本定律
1. 光的直线传播定律
2. 光的独立传播定律
3. 光的反射和折射定律
(1) 反射定律
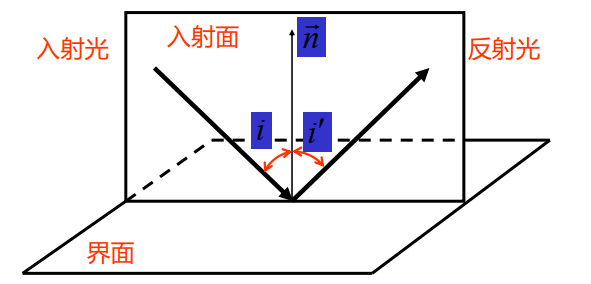
反射光在入射面内;
反射角等于入射角,
(2) 折射定律

折射率的定义:
折射率
大的介质称为光密介质,小的称为光疏介质.
折射光在入射面内;
入射角的正弦与折射角的正弦之比,对于给定介质及光波长,是一个常数,
有斯涅尔(Snell)定律
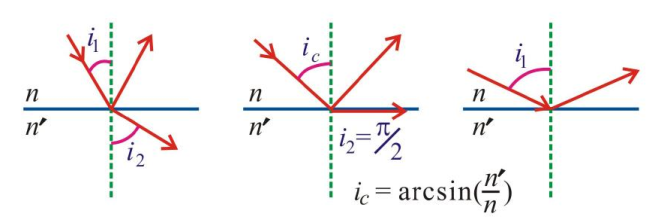
重要例子:全反射原理,当光从光密介质射到光疏介质表面时,可能会出现全反射现象.
1.2.2 费马原理
光程:光在均匀介质中通过的几何路径
光在介质中走过的光程等于以相同的时间在真空中走过的距离,即
费马原理的表述:
空间两点间的实际光线路径是光程为平稳值的路径. 这里,”平稳“指的是当光线以任何方式对该路径有无限小的偏离时,相应光程的一阶改变量为零,即
空间中两点的实际光线路径,与其他相邻的可能路径相比较,其光程(或传播时间)取极值.
因此,费马原理也称为光程极值原理或时间极值原理. 多数情况下,指最小值,故该原理又曾称为最小时间(或光程)原理.
意义:描述光线传播行为的普遍规律.
例子:直线传播定律,
反射定律
折射定律
1.2.3 光学成像
1. 薄透镜近似
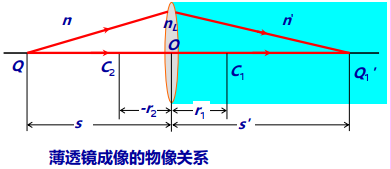
薄透镜成像的物像关系:
其中
2. 薄透镜的焦点与焦平面
空气中的薄透镜:
3. 高斯物像公式
1.3 光是电磁波
单色光波及其描述
单色光波的四个条件:
空间格点的电磁场以同一频率做简谐振荡;
各点的振幅不随着时间变化;
初相位是空间分布,与时间无关;
波列在空间上无限延伸,在时间上无限长.
在均匀介质中,沿
波面(等相面):波场中相位相同的点的集合.
平面单色波:波面是平面的单色波.
沿着任意方向传播:
特别,若沿着
其中,
称为波矢,其方向指向波的传播方向.
简谐波的复数表示式
包含时间变量和空间变量的两部分完全分离开.
称为复振幅. 其模量
平面波的复振幅
球面波的复振幅
1.4 光的干涉
发生条件
必要条件:
频率相同(适用于所有波动);
振动方向一致或有平行的振动分量(仅适用于矢量波);
相位差在观察时间内稳定分布(尤为重要);
充分条件:参与相干的光振幅大致差不多.
杨氏双缝干涉
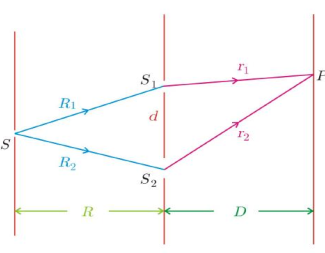
相邻两条明(暗)条纹的间距
其中
薄膜干涉
等厚干涉
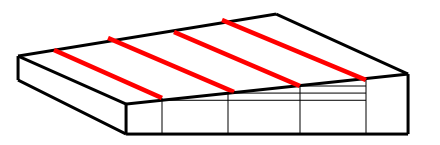
垂直入射,厚度相等的地方,是同一级亮条纹,故称等厚干涉.
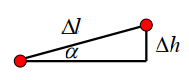
相邻条纹的厚度差
条纹间距
即干涉条纹是一系列等间距的平行直条纹.
牛顿环

高度
,即 . 借助 即得.
亮条纹的位置:
暗条纹的位置:
明环半径:
暗环半径:
图样特点:
干涉图样圆环半径越大,相应的干涉级越高;
间距不等,随着圆环半径增大,条纹变密;
从反射光中观测,牛顿环的中心点是暗点;从透射光中观测,牛顿环的中心点是亮点.

应用:测量透镜的曲率半径.
测出任意两级暗环的半径(或直径),数出它们的级数差
若
增透膜和增反膜
利用薄膜干涉提高光学器件的透光率.
1.5 光的衍射
特点
衍射效应与某种复杂的干涉效应有关系;
限制与扩展;
衍射效应的强弱与障碍物线度
巴比涅原理
互补屏产生的衍射场复振幅之和等于自由传播时场的复振幅,即
两互补屏在后焦面上产生的夫琅禾费衍射强度完全相同(像点除外).
夫琅禾费圆孔衍射
艾里斑
半角宽度(角分辨极限)
其中
半径(线分辨极限)
1.6 光的偏振
分类
线偏振光
圆偏振光
椭圆偏振光
自然光
部分偏振光
偏振度
偏振光的合成
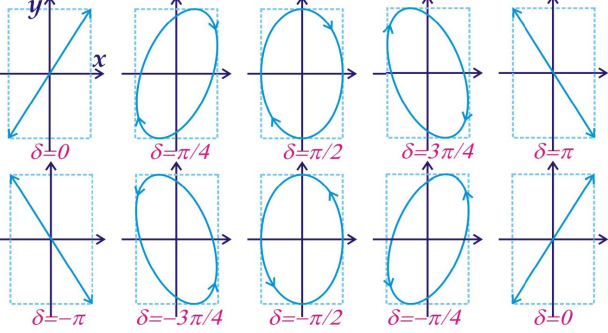
偏振片对不同偏振态的光强响应
线偏振光:马吕斯定律,
光的散射
应用:
自然光经散射,一般将变为部分偏振光,雨后初晴出现的虹和霓也是部分偏振光;
直视太阳,进入眼睛的主要是被大气散射之后透射过来的光;
巡视天空,进入眼睛的是阳光经大气散射之后的光;
蓝天,瑞利散射;
白云,米·德拜散射.
1.7 黑体辐射
Stefan-Boltzmann 定律
辐射的总能量(曲线下的面积)与
其中
Wien 位移定律
曲线的极大值满足
其中
用于测量温度,
Rayleigh-Jeans 定律
电磁学和统计物理严格求解得
普朗克能量子假说
空腔中的驻波是一系列的谐振子,只能取一些分立的能量,
其中
黑体的辐射本领为
1.8 光电效应
光电效应的解释
光子的能量
光电效应方程
光的波粒二象性
光子能量:
光子质量
光子动量
粒子性:一个光子是一个不可分割的主体;
波动性:具有波的特征,
光同时具有粒子性和波动性.
de Broglie 的物质波
所有的波都具有粒子性;
所有的粒子都具有波动性;
不能将物质的运动和波的传播分开.
第二章 波尔原子模型
2.3 波尔氢原子理论
2.3.2 波尔氢原子模型
1. 波尔假设
定态假设:原子的能量状态是分立的,电子只在某些特定的轨道上运动,每个轨道对应一个定态
角动量量子化假设:电子处于上述 定态时,角动量是量子化的,
频率条件:当电子吸收或放出能量时,它会在不同轨道间发生跃迁,跃迁前后的能量差满足
2. 波尔模型
(1) (类)氢原子的大小
则量子化的轨道半径为
相应的轨道速率为
其中精细结构常数
当
轨道半径
波尔速度
(2) (类)氢原子的定态能量——量子化的波尔能级
其中
(3) (类)氢原子的光谱
光谱公式
当
其中里德伯常量
2.3.3 波尔原子模型的问题
经典和量子并存;
预言了发射和吸收光子的频率,但是光谱线的强度、极化、选择定则不能解释;
无法解释更复杂的光谱现象.
第三章 波函数与测量
3.2 波函数的物理意义
3.2.1 定义
其中
波的强度或振幅反映的是粒子在时刻
3.2.2 对波函数的要求
单值
有限
连续
粒子不能湮灭,即总能在空间某处发现该粒子,
3.2.3 波函数的归一化条件
其中
3.2.4 态与态叠加原理

3.3 不确定关系
3.3.1 海森堡不确定性原理(测不准原理)
若两个力学量
3.3.2 物理含义
物质不可能同时具有确定的空间位置和动量;
能级的自然宽度,

束缚粒子的平均最小动能,

3.4 薛定谔方程
必须满足德布罗意关系式
条件:没有粒子的产生和湮灭现象,速度足够小;
薛定谔波动方程描述了一个质量为
自由粒子的薛定谔方程
对于处在势场
对于定态势能场
其解为
3.5 力学量的算符表示
平均值
此外,涨落
算符
本征函数与本征值
Hamilton 量
Hamilton 算符
Hamilton 方程
亦即
这里,
3.6 一维定态问题
列出一维定态薛定谔方程
根据波函数标准条件求出本征值
边界条件
波函数连续
波函数一阶微商连续
(非必须)归一化条件
写出定态波函数即得到本征值
通过归一化确定归一化系数
第四章 氢原子
4.1 氢原子定态函数
单原子电子的波函数
由库仑势
得 Hamilton 算符
从而得到定态薛定谔方程
解得氢原子的波函数
其中
对每一个
对每一个
原子物理中,有时候用不同的字母来标记同一主量子数下不同原子外层的电子轨道. 它们与角动量量子数之间的对应关系为
| 字母 |
4.2 量子数的物理解释
用一组量子数描述原子的状态:
1. 主量子数
主量子数
当
其中
为精细结构常数.
不同的状态可以具有相同的能量,这称为简并. 根据
对每一个
对每一个
对于一个
即一个
2. 轨道角动量量子数
对
又因为
即,
角动量
量子态为
3. 磁量子数
即
轨道角动量矢量在空间的某一特定方向(如
特定方向
4. 角动量的矢量模型
由前,波函数
由于角度函数均可以表示成
例如,对下面的波函数有
由此可以计算各本征值出现的概率:
对
对
从而
从而
从而
角动量的三个分量
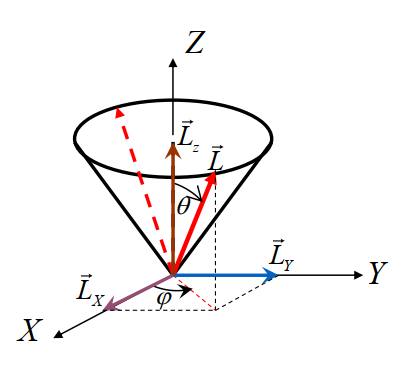
由
得
对于具有相同
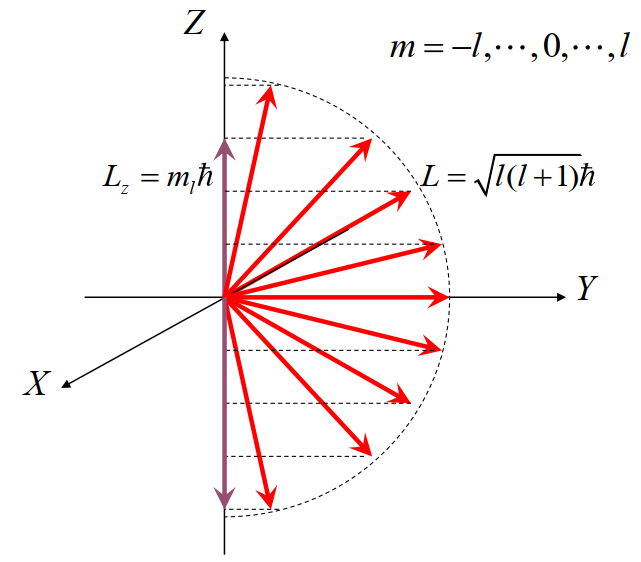
由
4.3 与波尔模型的区别
波尔假设(详见2.3.2):
定态假设;
角动量量子化假设;
频率条件.
区别:
电子没有确定的轨道,而是以概率的形式分布在经典轨道附近(波尔假设:原子的能量状态是分立的,电子只在某些特定的轨道上运动,每个轨道对应一个定态
能级量子化自然出现,且与实验有着更好的符合精度;
总轨道角动量取值为
4.4 跃迁概率和选择定则
1. 原子处在定态时不发射电磁波
薛定谔理论:定态时原子的电荷密度(概率密度)不随时间变化;
电磁理论:一个稳定的电荷分布体系是不会发射电磁波的.
所以,定态时原子是不辐射电磁波的.
2. 原子跃迁和叠加态
则叠加态
是薛定谔方程的解.
原子的跃迁过程中,
观察得混合态(非定态) 时原子的电荷分布将随时间振荡,故原子必定会辐射. 光子与原子发生共振相互作用,使原子感应出同频率的电荷振荡,这种振荡即为混合态的特征,
3. 跃迁率、平均寿命与谱线宽度
跃迁率
平均寿命
能级宽度
具有有限寿命的系统的能量必有一不确定值,所以原子发射的光谱线必有一定宽度,这就是自然宽度.
4. 跃迁的选择定则
选择定则:当初态和末态的量子数满足
时,电偶极矩的振幅不为零,此时的跃迁称为容许跃迁.
不满足选择定则的跃迁称为禁戒跃迁.
第五章 自旋
5.1 电子自旋的发现及性质
1. 轨道磁矩
轨道磁矩
其中
其大小为
原子磁矩的最小单位为玻尔磁子
由此,
磁矩总是和角动量联系在一起的.
2. 塞曼(Zeeman)效应
在磁场中,光谱线发生分裂,原来的一条谱线分裂为多条,且均为偏振光.
基于量子理论的解释:
原子的状态由三个量子数决定;
无外场时,原子的能量对磁量子数简并;
存在外场时,由于原子磁矩和外场的作用,不同磁量子数在磁场中的势能不同,发生能级劈裂.
结论:
证实了空间量子化,原子的磁矩在磁场中智能有几个离散的不连续的取向;
通过对原子束线通过不均匀磁场后的位移的定量计算,可以测量原子磁矩;
氢原子基态同样会发生分裂,测量到的磁矩为一个玻尔磁子,这只能是电子本身磁矩的贡献.
3. 电子自旋假设
内容:
每个电子都具有内禀角动量,即自旋
每个电子均有自旋磁矩
其中
注意:电子轨道运动产生的磁矩和自旋产生的磁矩有本质的不同,前者的
自旋是微观粒子的本性,是一种与空间自由度无关的内禀运动,自旋变量只能取离散的数值. 自旋不是机械运动.
5.2 自旋和轨道相互作用
1. 自旋-轨道耦合能
原子内部由于带电粒子的运动,会产生磁场,即原子的内磁场. 电子处在这内磁场中,其自旋磁矩与磁场发生相互作用,由此引起能级的分裂. 自旋-轨道相互作用是磁相互作用,这种作用较弱,只使原子能级发生细微的改变,从而产生精细结构.
具有自旋磁矩的电子,在内磁场中具有势能,使电子有一附加能量
电子的自旋量子数
2. 总角动量和原子磁矩
总角动量
原子中的电子具有轨道角动量
的大小以及它们的
自旋-轨道相互作用的存在,各自处在对方的磁场中使
定义
其中
多重态结构的原子态的符号表示:
不同的量子数反映了不同运动状态和不同能量状态. 没有外磁场时,具有相同的
例如,
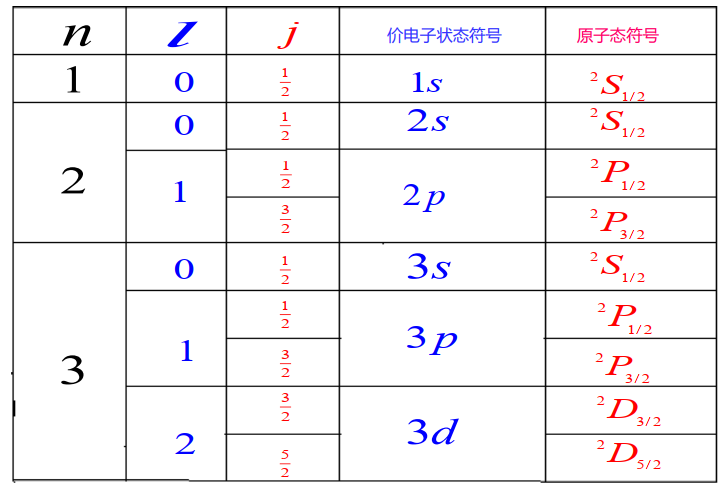
电子自旋量子数
原子磁矩
总磁矩只需要考虑轨道磁矩和自旋磁矩,
称为原子的有效总磁矩. 在讨论弱磁场中的原子时,可用
表示有效磁矩与总角动量之比,其中
有效磁矩
3. 自旋-轨道相互作用(耦合能)对能级的影响
故只要知道了各个量子数(确定了原子的状态),便可以计算出自旋-轨道相互作用能. 其中,
也可以表示成
具有较大
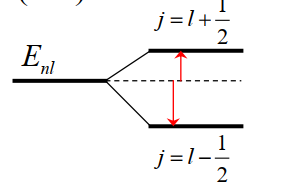
注意
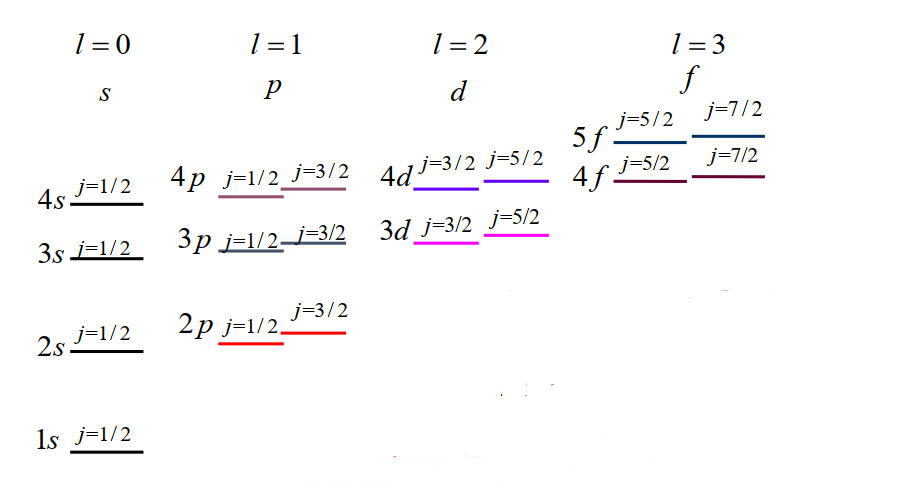
注意到
故量子数越大,能级分裂越小.
5.3 狄拉克记号与量子力学基本假设
量子力学有两种等价的形式表达:
以薛定谔方程为基础的微分方程形式;
海森堡提出的矩阵力学形式.
线性代数回顾
的标量
联系:本征值与本征波函数.
狄拉克记号
狄拉克右矢
例如考虑粒子处在上或下能级,
如果认为粒子处在上下能级的可能性各是一半,那么整体的状态就可以表示为
这是一个纠缠态,准确讲是涉及微观和宏观的一个纠缠态,可见以狄拉克符号标记物理系统量子状态可以更突出物理.
按照归一化要求,
狄拉克右矢的标量积
对每一对狄拉克右矢
狄拉克左矢及狄拉克右矢的内积
狄拉克左矢则表示相应右矢的厄密共轭,即
态矢量
其一般为复数,且满足
结论:右矢类比列向量,左矢类比其转置共轭即行向量,
直积态
对两个独立的量子系统
其矩阵运算形式举例:假定
复合系统的基矢量记为
算符
算符
任何对量子态的改变都对应着某种运算,将其记为算符,即算符作用到右矢表示的量子态上,代表着 Hilbert 空间中的一种变换操作
运算规律
线性性:
单位算符:
算符相等:若算符
算符的和:
结合律和交换律:
注意:算符乘法没有交换律,即
矩阵表示
若将
对易关系和反对易关系
一般情况下,
如果
算符的逆
在有限维 Hilbert 空间中,算符可以用对应的矩阵表示. 如同给定矩阵的逆矩阵不一定存在一样,给定算符的逆算符也不一定存在.
如果某个给定算符
性质:
算符与其逆算符对易,即
伴随算符
在 Hilbert 空间中,算符
那么在其对偶空间(左矢量所在空间)中定义算符
由定义可知:
伴随算符对应于原算符矩阵的转置共轭矩阵.
性质:
证明方法,以第一条为例:对任意量子态
狄拉克标记的伴随
右矢和左矢的外积对应算符,内积对应复数. 例如,
性质:
厄密算符
厄密算符又称为自伴随算符,即满足转置共轭等于自身的算符,是用于表示力学量的算符,
根据量子力学的测量公设,对量子态进行可观测力学量
对于任意量子态,厄密算符的期望值为实数;对于任意量子态,若算符对应的期望值均为实数,则该算符必为厄密算符.
表象
算符运算


上述方程有非零解,要求
解这个关于
得到若干个关于
量子力学公设体系
区别经典力学与量子力学:
经典力学:
粒子的位置和动量在任何时刻可以确定给出;
运动规律由牛顿运动方程给出;
轨道
量子力学:
微观粒子不能同时具有确定的位置和动量;
具有波粒二象性,状态由复变量波函数完全描述;
运动规律由薛定谔方程给出;
对粒子实施某个力学量的测量仅能给出统计分布(统计诠释).
第一公设:波函数公设
内容:
一个微观粒子的状态总可以用一个波函数
波函数模的平方
如果
要点:
状态必由波函数完整描述;
波函数的概率诠释;
波函数的物理约束;
状态叠加原理.
第二公设:算符公设
内容:
任何一个可观测力学量
算符是施加在描述状态的波函数上的操作;
厄密算符的本征值为实数,对应物理量的观测值为实数;
可观测力学量的本征函数集满足正交完备性,构成一个表象.
要点:
力学量用算符表示;
算符是线性的;
本征值为实数;
表象理论.
第三公设:测量公设(期望值、投影和测量坍缩)
内容:
一个微观粒子系统处于波函数
特别当波函数是归一的时,就有
单次测量结果只能对应可观测力学量算符
对于非简并的本征值
对于存在简并的本征值
定义投影算符
满足
对处在
本征值非简并时,即坍缩到
第四公设:微观系统动力学演化(薛定谔方程)
内容:
描述微观粒子物理状态的波函数随时间的演化遵循薛定谔方程
用状态矢量和力学量算符表示为
其中
第五公设:全同性假设
内容:
属于同一类的粒子称为全同粒子,也就是说固有性质(质量、电荷、自旋、同位旋、宇称、奇异数等)相同的粒子称为全同粒子.
全同性原理:在全同粒子组成的体系中,交换两个粒子后微观系统的状态波函数是对称或反对称的;
但波函数的模平方始终是对称的. 对任意观测量进行测量,结果不变,即不出现可观测的改变,这称为不可分辨性;
在时空交叠的区域即波函数出现交叠的部分,全同不可分辨的粒子会体现复振幅的相干叠加,会有相长干涉和相消干涉现象.
5.4 自旋算符与泡利矩阵
引入自旋角动量算符
自旋算符本征值、本征态及自旋表象
类似于轨道角动量,
而实验上测量到的
泡利算符
为了描述方便,引入泡利算符
在
显然,它们是厄密矩阵,相互反对易.
自旋在任意方向投影的波函数
考虑泡利算符
将
其中
5.5 磁场下电子自旋的进动与自旋转动算符
在外磁场中,若电子的轨道运动和自旋运动可以分离,仅考虑自旋磁矩的受力,此时电子的 Hamilton 算符为
其中
电子在磁场中运动满足薛定谔方程
其中
借助泡利算符的性质,有
5.6 Bloch 球与自旋体系动力学
泡利算符
其中
任意自旋量子态
自旋空间中所有量子态构成三维空间中的一个单位球球面,球面上每一个点(对应的矢量
系统在 Hamilton 算符控制下演化对应于操作
其物理意义就是将量子态绕轴
5.7 粒子全同性、波函数对称性及泡利不相容原理
全同性原理
由全同粒子构成的系统,交换两个粒子并不导致可观测的物理效应,但会导致描述系统状态的波函数发生改变.
波函数对称性
设两粒子的波函数为
后系统应恢复原状态,即
泡利不相容原理
原子内没有两个电子具有相同的电子状态,即没有两个电子具有四个全同的量子数.
结论:原子内的多电子波函数满足交换反对称.
引入自旋后,原子波函数需要修正,氢原子的波函数
则确定的轨道
元素周期表中各原子的核外电子填充规则:
电子优先填充能量低的轨道;
对于简并的轨道,电子先尽可能每个轨道单占据;
但占据时电子的自旋方向相同(最大角动量,降低系统总能量);
如果占据后有多余电子,电子再选择双占据,双占据电子自旋方向相反.
第六章 二能级体系与量子比特
6.1 二能级系统及其操控
理论
系统的 Hilbert 空间是二维的,因此可以用一组二维正交完备基
叠加系数也可以用参数
矩阵表示:
Bloch 球表示:
实验:二能级系统在光场驱动下的 Rabi 振荡(光与原子的相互作用)
Rabi 振荡和光场的振幅大小(强度)和频率皆有关:
光场振幅越大,Rabi 频率振荡的频率越大;
光场频率和原子能级间隔对应的频率越接近(即越接近共振),Rabi 振荡的振幅越大.
6.2 纯态、混合态与密度算符
纯态与混合态
光子的等效(赝)自旋空间:偏振,
水平偏振(horizontal):
垂直偏振(vertical):
椭圆偏振光:
密度算符
性质:
厄密性:
正定性;
无论是纯态还是混合态都有
可以幺正对角化,本征值非负,本征值之和为
纯态:
区分纯态和混合态:
纯态
混合态
6.3 量子比特
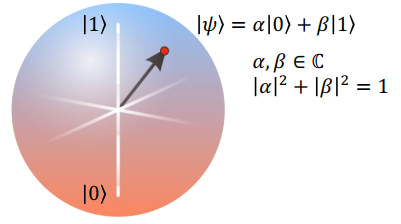
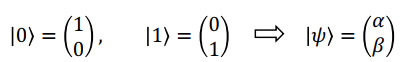
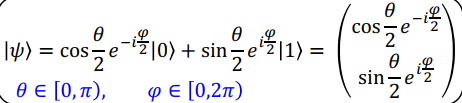
拥有更多的可能状态;
这些状态可用 Bloch 球上的一个矢量表示;
指向南北极的矢量分别表示状态
对应二能级系统或自旋的某一个状态;
需要通过量子测量完成经典信息的提取.
量子比特的操作

物理实现(以光子偏振态为例)

本征值分解:建立晶体坐标系与实验坐标系的对应及其反变换,

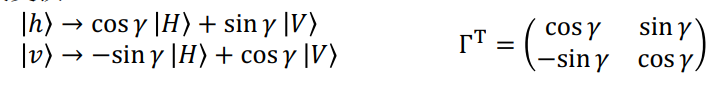
晶体坐标系下的演化:波晶片实现的是晶体两个本征态之间的相位门,即在
任意量子比特的演化:
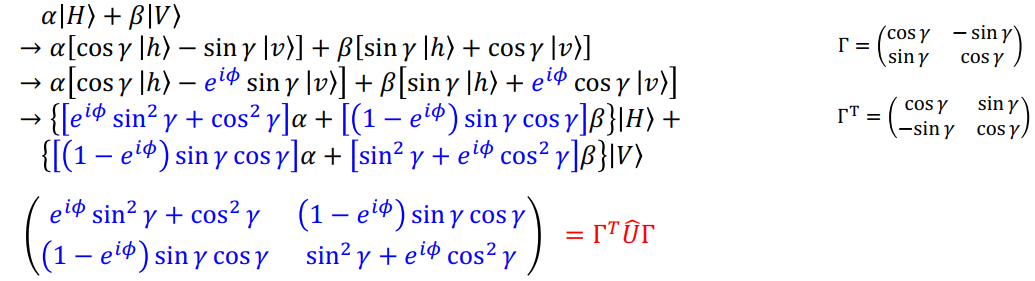
单量子比特的操作对应 Bloch 球上的绕轴旋转
其中决定旋转轴
量子比特的纯态与混合态
任意一个 Qubit 空间(2 能级空间)的密度算符对应于
其中
对于纯态:
对于混态:
对于最大混态,
量子不可克隆定理
内容:不存在这样的克隆机(cloning machine),完成某种幺正操作
证明:
首先假定这样的克隆机存在,即可以进行未知量子态的拷贝. 对于任意两个量子状态
计算左侧两个状态的内积,即
计算右侧两个状态的内积,即
两侧相等意味着
这意味着
物理意义和应用:
是量子物理的一个重要结论,即不可能构造一个能够完全复制任意量子比特而不对原始量子位元产生干扰的系统;
量子力学的线性特征是这个原理的根本原因;
是量子信息学的基础. 量子信息在信道中传输,不可能对第三方复制窃取信息而不对量子信息产生干扰,这个原理是量子密码学的基石.
第七章 量子信息简介
7.1 量子纠缠与 Bell 不等式
量子态叠加原理
量子系统(光子,电子,核,原子等)可能存在如下状态:
其中
量子纠缠
考虑两个电子自旋系统或两量子比特系统,其 Hilbert 空间可以采用非耦合表象
若两个系统各自有确定的量子状态
如果两粒子系统的整体波函数不能写成各自确定状态(纯态)直积的形式,则称该态为纠缠态,否则称为可分态.
严格数学定义:
由多个子系统构成的复合系统,存在量子纠缠当且仅当其密度算符不能写成子系统密度算符直积求和.
考虑包含两个子系统的情形,纠缠态就是不能写成如下形式的态:
能写成上述形式的态称为可分态.
处于纯态的复合系统存在纠缠当且仅当不能写成如下形式
Bell 不等式
7.2 量子通信
量子秘钥分发
BB84方案:
状态的编码集合:光子四种偏振状态

分属两组共轭基.
态内的两个态正交,不同组内的态不正交,
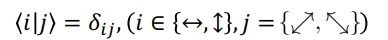
两组基互为共轭是指,每一组基的任一基矢量在另一组基的两个基矢量上的投影相等,

量子隐形传态

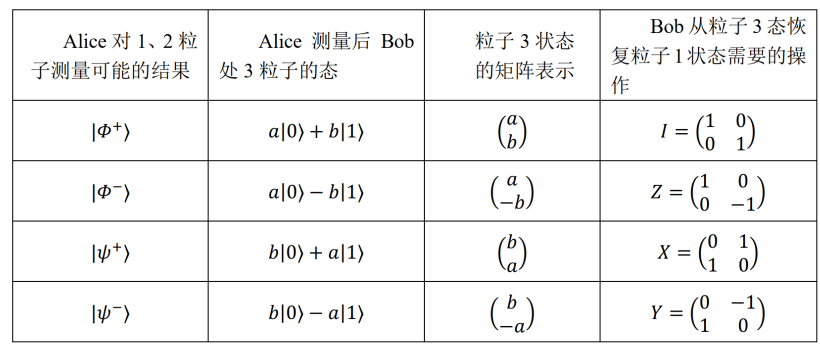
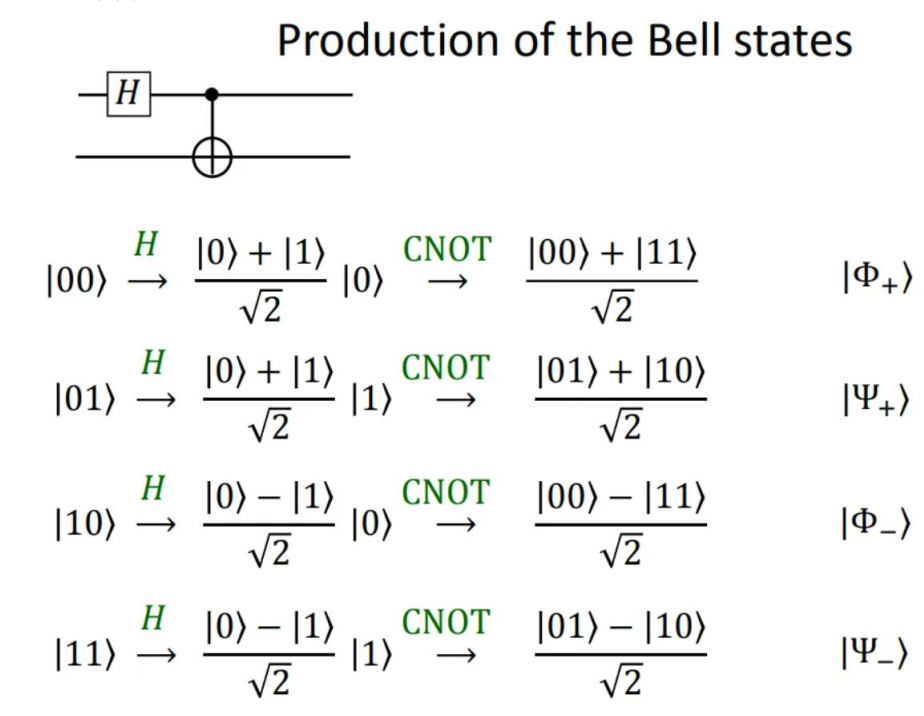
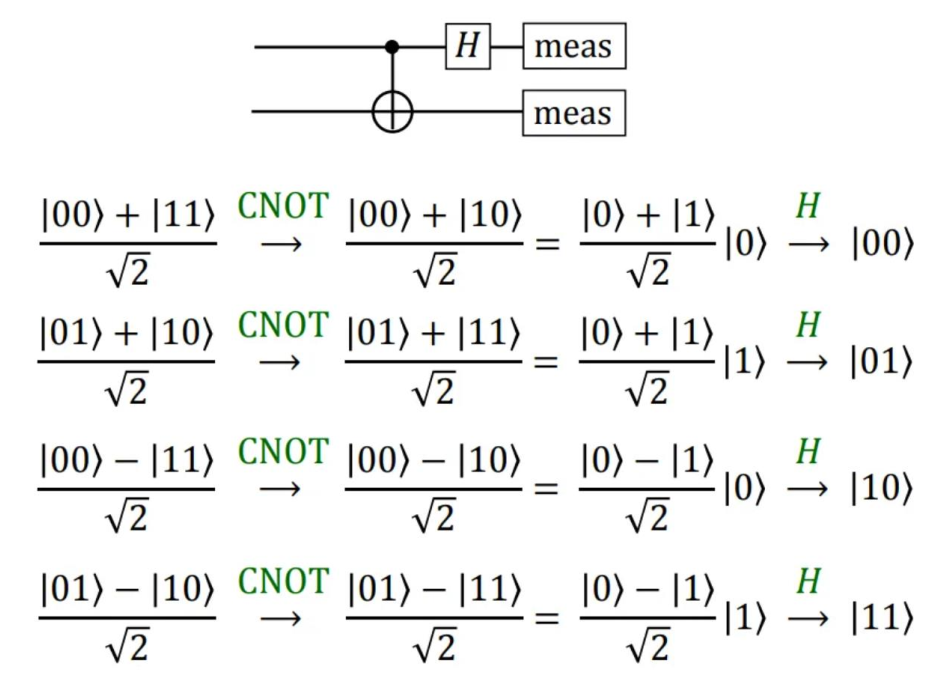
7.3 量子计算