概率论与数理统计
HW1
T1.2

(1)
(2)
是“三次均未击中目标”的对立事件,即
(3)
“第一次击中”为 ,而“第二次、第三次至少有一次击中”(记为)是“第二次、第三次均未击中”的对立事件,即
从而
(4)
“最多击中一次”是“三次均未击中目标”和“仅有一次击中目标”的和事件,即
T1.8

所求事件为 . 由容斥原理(inclusive-exclusive principle),有
T1.12

记 为“甲胜利”.
考虑三局两胜制,则 相当于“连胜两局“与”前两局中甲乙各胜一局且第三局甲胜”的和事件,记为 ,则
考虑五局三胜制,则 相当于"甲连胜三局"、“前三局甲胜两局乙胜一局且第四局甲胜”与“前四局中甲乙各胜两局且第五局甲胜”,记为 ,则
考虑 ,则
从而 在 单调减,在 单调增,又因为 ,在 上有 ,从而 ,即
即在 时,五局三胜制更有利.
T1.13

设 为“甲掷了 次硬币后出现正面”,则 ;
设 为“甲从第 个盒子中抽到白球”,则 当且仅当时取等;
设 为“甲掷了 次硬币后出现正面并胜利”,则
设 为“甲胜利”,则
事实上,有 . 综上,这规则对乙更有利.
T1.17

设下午 已经发出第一辆公交车,则给定时间内的发车时间为下午 、、 和 .
以下午 为基准时间,设甲、乙的到达时间分别为 和 ().
记 为“甲、乙同乘第一辆车”,则
同理,
易知
记 为“甲、乙同乘一辆车”,则
T1.20

考虑掷一六面质地均匀骰子. 设 掷出的倍数,掷出,掷出的倍数,则
有 和 ,但有 .
T1.23

(1)
记 为所求事件,则
(2)
设谣言传播了 次,则:
当 时,
当 时,显然有 .
(3)
(3.1)
记 为所求事件,则
(3.2)
设谣言传播了 次,则
当 时,
当 时,显然有 .
T1.24

(1)
考虑从第一箱中取,则第一次取取到一等品的概率为 ;
考虑从第二箱中取,则第一次取取到一等品的概率为 .
记 第一次取到的零件是一等品,则其概率为
(2)
记 第二次取到的零件是一等品,则 两次取到的零件都是一等品.
考虑从第一箱中取,则两次取到一等品的概率为 ;
考虑从第二箱中取,则两次取到一等品的概率为 .
从而,
所以有
T1.30

Bayes 公式:设 , 是 的一个划分,,则
测出阳性,带菌,不带菌. 则 ,,,.
(1)
(2)
第次测出阳性 两次均测出阳性,则 .
,.
T1.33

记 从甲袋中取个白球和个黑球放入乙袋,从乙袋中取出白球,则 是样本空间 的一个划分.
,,;
,,.
(1)
考察全概率公式.
(2)
考察 Bayes 公式.
首先计算“已知从乙袋中取出的球为白球,从甲袋中取的两球中无白球”的概率,也就是 .
所求概率为其对立事件的概率,则
HW2
摆了
HW3
T2.22

T2.27

固定 ,令 ,则 .
由题意,设 ,则
令 ,则
即 、.
这个结论与 的取值无关,故
又因为
计算得 ,即 . 同时,
易知 服从 上的均匀分布.
T2.37

(3)
设 . 在 分别单调减.
在 上, 有唯一反函数 ,其导函数 连续,则
在 上,同理可得
此时由密度变换公式,
不妨定义 ,这对分布函数没有影响. 此时,
从而, 与 具有相同的分布.
HW4
T2.40

由 ,其概率密度函数为 ,其分布函数为
(1)
在 上严格单调,其反函数 可导,. 故概率密度函数为
(2)
在 上严格单调,其反函数 可导,. 故概率密度函数为
(3)
在 上严格单调,其反函数 可导,. 故概率密度函数为
T2.42

是严格单调连续函数. 又因为 为分布函数,一定为非减函数,从而一定是增函数.
随机变量函数 的分布函数为
又因为 严格增,则 ,则
又因为分布函数的值域为 ,得 .
概率密度函数为 . 从而,随机变量函数 服从区间 上的均匀分布.
T2.44
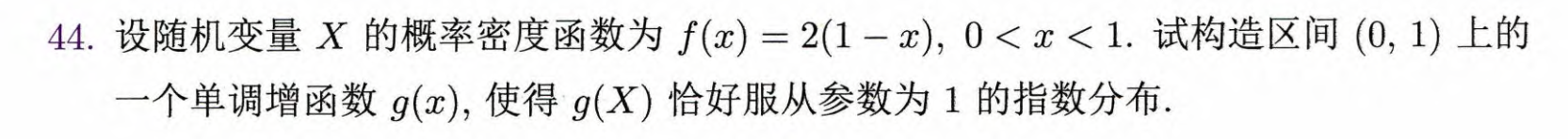
服从参数为 的指数分布,则
其分布函数为
设 存在反函数 ,则 ,则
两边求导得
取 ,得
且
即 为所求的在区间 上的单调增函数.
T2.48

由 得
从而
(1)
在区间 上,随机变量函数 的分布函数为
从而,
的分布函数为
(2)
记 ,,,,则 构成了 的一个划分.
由全概率公式,
T2.49

由 ,其概率密度函数为 ,其分布函数为
(1)
,则随机变量 的分布函数为
其概率密度函数为
(2)
则
所以,分布函数为
(3)
在区间 上分别严格增.
在区间 上,,其有唯一反函数 ,其导函数
连续,则
在区间 上,,其有唯一反函数 ,其导函数 连续,则
当 时,. 由密度变换公式,
当 时,. 由密度变换公式,