概率论与数理统计 公式
这里将重点放在公式本身,一些不太重要的条件会忽略掉.
杂七杂八
函数
借助 函数计算与正态分布有关的矩:
.
含参变量积分的可微性
特别,
此时也可以从另一个角度考虑:
事件及其概率
条件概率
定义:
乘法公式:
全概率公式:
其中 是样本空间 的一个划分.
贝叶斯公式:
特别,
随机变量及其分布
离散型随机变量的分布
两点分布(伯努利分布)
或 离散均匀分布
超几何分布
, 条鱼、 条被标记、捞 条鱼,
二项分布
,
负二项分布
负二项分布(帕斯卡分布)
,
几何分布
取 ,,
几何分布有无记忆性,
泊松分布
定义:,
泊松逼近定理:
,,
实际应用:, 时即可应用;当 时, 情况下仍有较高的精度.
连续型随机变量的分布
均匀分布
,
指数分布
,
指数分布有无记忆性
一个非负连续型随机变量,如果具有无记忆性,那么其分布必为指数分布.
正态分布
,
,
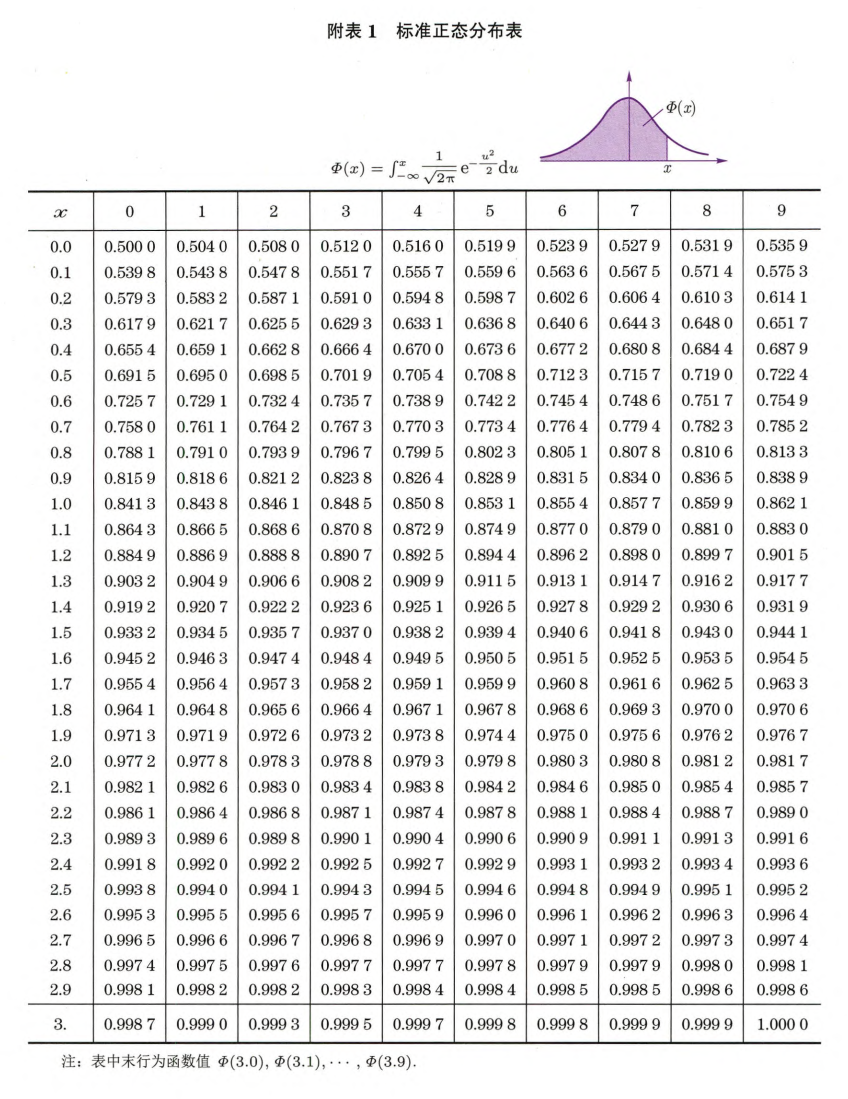
标准化变换:,,
随机变量函数的分布
离散型随机变量函数的分布
略.
连续型随机变量函数的分布
定义:,
密度函数变换公式:
严格单调且反函数可导,
其中 为 的反函数,,.
若 逐段单调,
多维随机变量及其分布
边缘分布
略.
条件分布
定义:
乘法公式:
贝叶斯公式:
随机向量函数的分布
,
,
,
这里 ,反函数记为 .
注意:当随机变量 相互独立时,有 ,计算会方便进行.
独立随机变量的和:
设随机变量 相互独立,分别具有概率密度函数 ,考虑 ,
指数分布随机变量的和( 分布)与差(拉普拉斯分布):
设 和 独立,均服从指数分布 ,,
,,
即 . 特别,.
分布对参数 具有再生性.
,
该分布称为拉普拉斯分布,即独立指数分布的差服从拉普拉斯分布.
正态分布随机变量的和:
设 和 互相独立,分别服从 和 ,则 .
正态分布 对参数 具有再生性.
独立随机变量商的分布:
设 和 相互独立,,,,
其中 .
特别,,,则
该分布称为柯西分布,即独立同正态分布随机变量的商服从柯西分布.
相互独立随机变量变量最大值和最小值的分布:
设 和 相互独立,,,求 和 的分布.
最大值:
推广到 个变量:
若再加上同分布的条件,
最小值:
推广到 个变量:
若再加上同分布的条件,
随机变量的数字特征和极限定理
数学期望
数学期望
定义:
性质:
条件数学期望
定义:
条件期望的平滑公式(全期望公式):
方差
方差和标准差的定义:
方差的性质:
马尔可夫不等式
切比雪夫不等式
若干分布的期望和方差总结
分布
,
或 离散均匀分布
意义不大.
超几何分布
,
二项分布
,
负二项分布
,
特别,对几何分布 ,
负二项分布的期望可以借助几何分布的期望,由期望的线性性得到;直接计算则相对麻烦.
泊松分布
,
均匀分布
,
指数分布
,
正态分布
,
矩
定义:
称为 关于 的 阶矩;
称为 的 阶原点矩,;
称为 的 阶中心矩,.
协方差
定义:
性质:
相关系数
定义:
,等号成立的充要条件是随机变量之间有严格的线性关系.
当 时,我们称 负相关;
当 时,我们称 正相关;
当 时,我们称 线性不相关.
有关正态分布随机变量的结论:
,则 ;
若 相互独立,则 ,反之不必成立. 但若 ,则 相互独立 .
对任何非退化的随机变量 存在方差,如下四个命题相互等价:
与 不相关;
;
;
.
熵
定义:
为离散型随机变量,
为连续型随机变量,
大数定律
依概率收敛:
设 是一随机变量序列, 为随机变量,如果 ,有
那么称随机变量序列 依概率收敛于随机变量 ,记为 或 .
(弱)大数定律:i.i.d. 随机变量序列的前 项部分和的平均 依概率收敛于 公共期望 ,即
伯努利大数定律:
设 为独立的 分布随机变量序列,则
中心极限定理
依分布收敛:
设 为一列实值随机变量, 为随机变量, 和 分别为随机变量 和 的分布函数. 如果对 的所有连续点 有
那么称 弱收敛于 ,也称 依分布收敛于 ,常记为 或 .
林德伯格-莱维中心极限定理:
设 是一列 i.i.d. 随机变量序列,记它们相同的期望和方差分别为 ,则部分和 标准化后的分布函数近似于标准正态分布函数,即
其中 .
棣莫弗-拉普拉斯中心极限定理:
设 是一列 i.i.d. 随机变量序列, 且 ,则 ,有
,因而棣莫弗-拉普拉斯中心极限定理告诉我们可以用正态分布来近似二项分布,即
统计学基本概念
基本概念
设 是从某总体 中抽取的一个简单样本,则常见的统计量包括:
样本均值
它反映了总体均值的信息.
样本方差
它反映总体方差的信息. 称为样本标准差,它反映了总体标准差的信息.
样本矩
称为样本 阶原点矩. 特别地, 即样本均值.
称为样本 阶中心矩.
当样本为简单随机样本时,由大数定律知 及 ,其他矩也依概率收敛到相应的总体矩.
抽样分布
分布
定义:
设样本 为来自标准正态总体的一个简单随机样本,
则 .
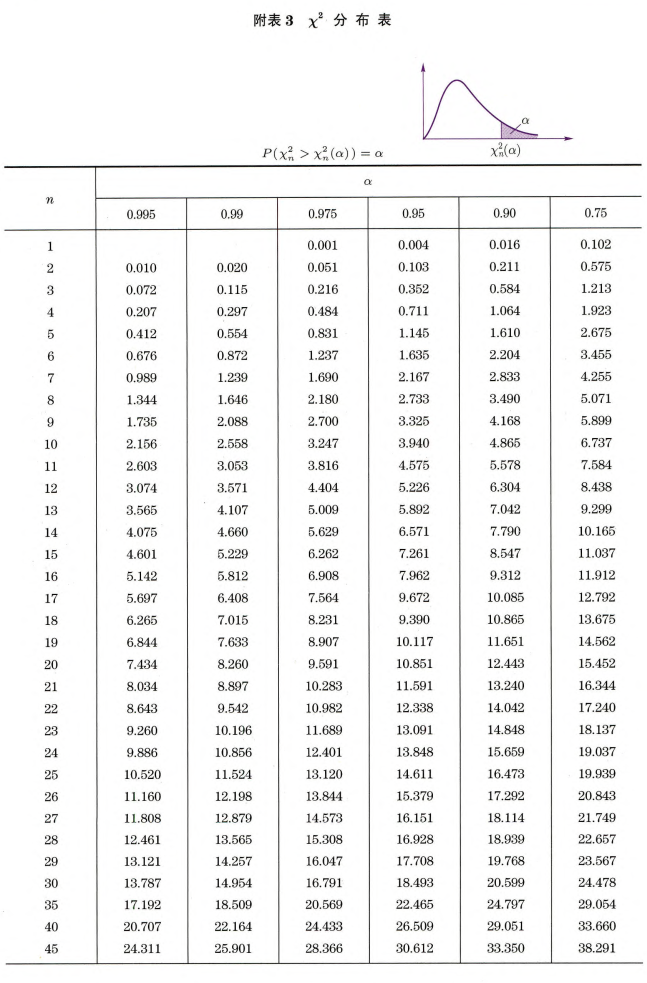
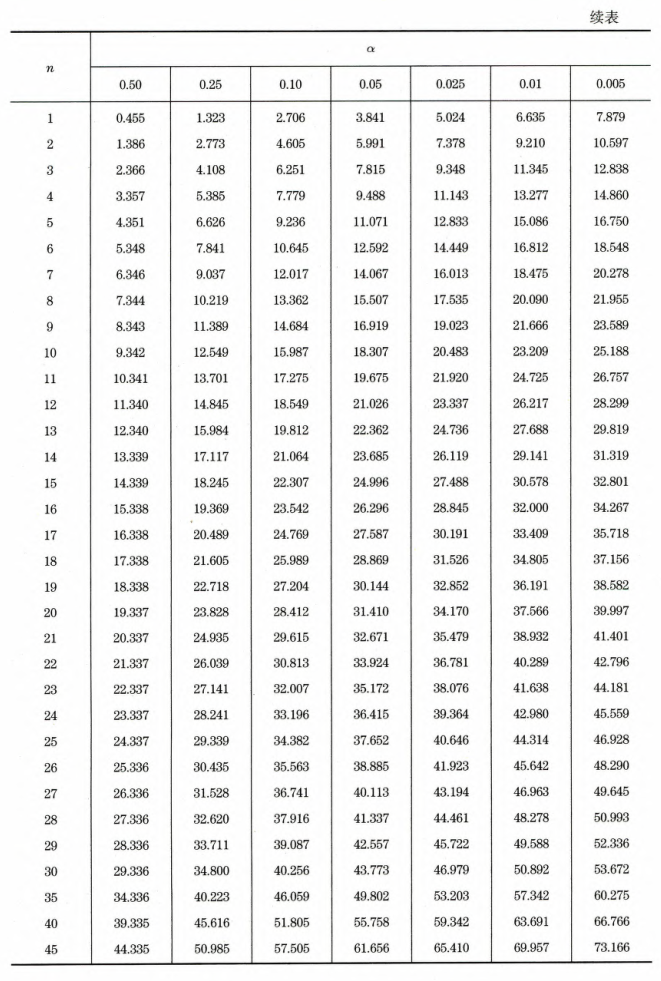
性质:
分布
定义:
设 ,且 相互独立,
则 .
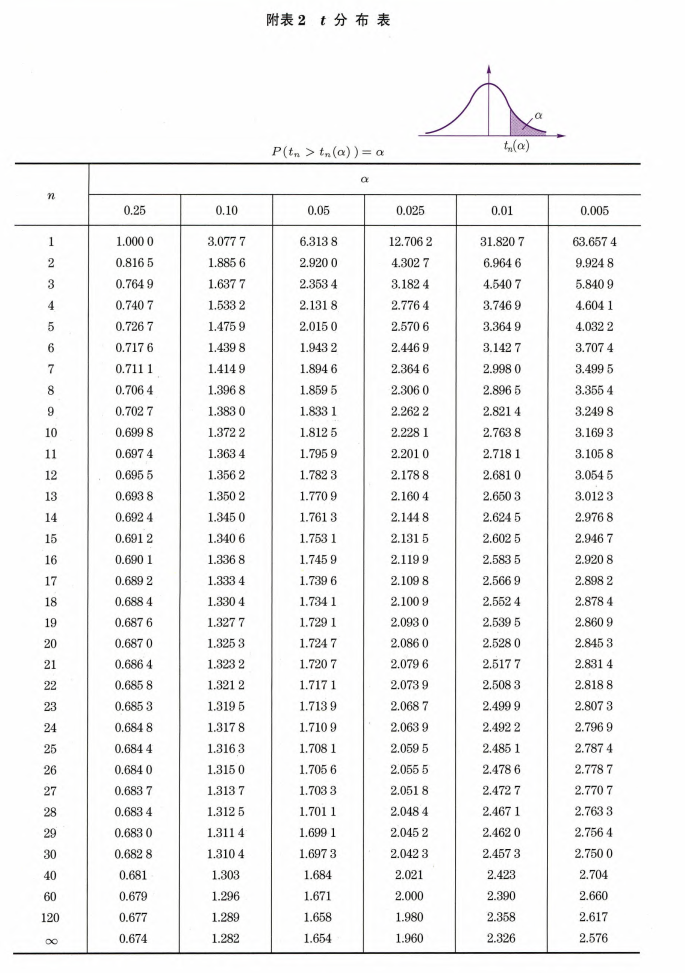
性质:
分布
定义:
设 ,且 相互独立,
则 .
性质:
若 ,则 ;
若 ,则 ;
.
其它
设随机变量 , 是不全为零的常数,则有
设 服从指数分布
则有
参数点估计
矩估计法
结论:
最大似然估计
结论:
优良性准则
点估计的无偏性
定义:
设 是 的一个估计量,称
为估计量 的偏差. 若对任一可能的 ,都有
则称 是 的一个无偏估计量.
结论:
是总体期望 的无偏估计. 特别,样本均值 在某种合理的标准下是最优的.
样本方差 是总体方差 的无偏估计. 矩估计(最大似然估计) 则不是无偏估计,它系统偏小.
样本标准差 不是总体标准差 的无偏估计,它系统偏小. 对正态分布,修正系数
无偏估计不总是存在.
最小方差无偏估计
有效性的定义:
设 都是总体参数 的无偏估计,方差存在,若
且至少存在一个 使上式不等号成立,则称 比 更有效.
点估计量的大样本理论
相合性
设 是参数 的一个点估计,若当样本量 时有
则称 是 的一个(弱)相合估计量.
(依概率收敛的定义见大数定律一节.)
渐进正态性
设 是参数 的一个点估计,设它的方差存在,记
若当样本量 时有
则称估计量 有渐进正态性.
区间估计
枢轴变量法
方法
设感兴趣的参数为 .
(1) 找一个 的良好点估计 ,一般为 的最大似然估计.
(2) 构造一个函数 ,称为枢轴变量,其中 为统计量,使得它的分布 已知,注意枢轴变量仅是 的函数,不能包含其他未知参数.
(3) 枢轴变量必须满足如下条件:,不等式 能改写为等价形式 ,其中 只能与 有关,与 无关.
(4) 取分布 的上 分位数 和上 分位数 ,由分位数定义,有
结论
正态总体均值 :
置信区间为 ,其中误差界限
已知未知未知总体不必为正态 其中前两种情况所用枢轴变量分别为
和
正态总体方差 :
枢轴变量为
置信区间为
两个正态总体均值差 :
两个正态总体方差比 :
枢轴变量
置信区间
大样本方法
比例 的区间估计
枢轴变量
置信区间(得分区间)的近似
一般要求 和 成立.
若要求得分区间的宽度为 ,解得样本量要求为
一般总体均值 的置信区间
枢轴变量
置信区间
置信限
对非正态总体,在样本量较大时候可以使用大样本方法寻求置信限.
假设检验
正态总体参数检验
单个正态总体均值的检验
已知
问题 1:
检验:
当时拒绝原假设否则不能拒绝
问题 2:
检验:
当时拒绝原假设否则不能拒绝
问题 3:
检验:
当时拒绝原假设否则不能拒绝 未知
问题 1:
检验为
当时,拒绝否则不能拒绝
问题 2,
检验为
当时,拒绝否则不能拒绝
问题 3,
检验为
当时,拒绝否则不能拒绝
当样本量 充分大时,由大数定律和中心极限定理,上面三类方差未知的检验中可以把 或 分别用 代替,而且此时的正态分布不必是正态分布.
两个正态总体均值差的检验
成组比较
设 是从正态总体 中抽取的一个简单样本, 是从正态总体 中抽取的一个简单样本,且两组样本相互独立,其中总体均值 未知,两个独立总体有相同的方差 , 可以已知也可以未知.
问题:
设 是给定的常数,考虑
;
;
.
在应用中常见的情况是 未知,.
已知:取检验统计量
三个检验问题的水平 的检验分别为
当时拒绝否则不能拒绝当时拒绝否则不能拒绝当时拒绝否则不能拒绝 未知:取检验统计量
其中
三个检验问题的水平 的检验分别为
当时拒绝否则不能拒绝当时拒绝否则不能拒绝当时拒绝否则不能拒绝
成对比较
构造虚构总体 ,样本 .
考虑如下检验假设问题:
;
;
,
其中 为虚构总体 的均值, 是最常见的.
正态总体方差的检验
单个正态总体方差的检验
考虑如下检验问题:
;
;
,
其中 为给定的常数.
其对应的检验分别为
当时拒绝否则不能拒绝 当时拒绝否则不能拒绝 当或时拒绝否则不能拒绝 两个正态总体方差比的检验
设 分别是从正态总体 和 中抽取的简单样本,且两组样本之间相互独立. 考虑如下检验问题:
;
;
,
其中 为给定的常数,常见的情况是 ,即两个方差相等.
记 和 分别为样本 和 的样本方差,则对应的检验分别为
当时拒绝否则不能拒绝 当时拒绝否则不能拒绝 当或者时拒绝否则不能拒绝 注意:.
比例 的检验
设 是 分布总体 的一个样本,关于 的常见假设有三种:
;
;
.
感觉最多考近似情形:当样本量 比较大(一般大于 ),
:当 时拒绝 ,否则不能拒绝 ;
:当 时拒绝 ,否则不能拒绝 ;
:当 时拒绝 ,否则不能拒绝 .
值
概念:
值得到当前样本下检验统计量的值或更极端值原假设下 取检验的水平为 ,当一个检验法则的 值不超过 时,检验统计量 的值落在了拒绝域内,我们即拒绝原假设;反之,则没有足够的证据拒绝原假设. 这样即得到一个水平 检验法则:
当值时,拒绝原假设 值表示了在当前样本下观察到的显著性水平. 值越接近 ,拒绝原假设的证据就越充分;反之, 值越接近 ,不能拒绝原假设的证据就越充分.
非参数假设检验
拟合优度检验
理论分布完全已知且只取有限个值
检验问题
统计量
检验为
当时,拒绝否则不能拒绝 拟合优度
越大,原假设成立时出现 这样大的差异就越不奇怪.
理论分布类型已知但含有有限个未知参数
检验问题
其中 都已知且两两不同,,且依赖于 个未知的参数 .
统计量
其中,为 的最大似然估计 , 为原假设 下参数 的最大似然估计.
检验为
当时,拒绝否则不能拒绝
当总体 取无穷多个值,但其分布中仅含有有限个未知参数,此时原假设可以表示为
其中 为未知参数,它们在一定区域内变化.
我们可以将总体的取值切为 段,记切分出的区间为
其中 ,则定义离散型随机变量
则当原假设 成立时,随机变量 的分布为
其中 .
这里是将检验假设 的问题转换为检验理论分布对应的假设 的问题.
列联表检验
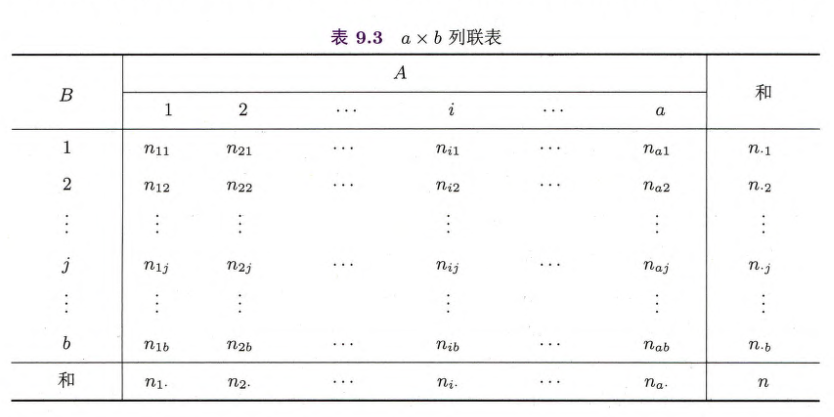
独立性检验
统计量
当 时, 的渐进分布是自由度为 的 分布,即 .
特别,对 列联表,
在原假设为真时依分布收敛于 .
齐一性检验
齐一性检验即检验某一个属性 的各个水平对应的另一个属性 的分布全部相同:
对齐一性检验问题,所构造的检验统计量 的极限分布仍是自由度为 的 分布.




