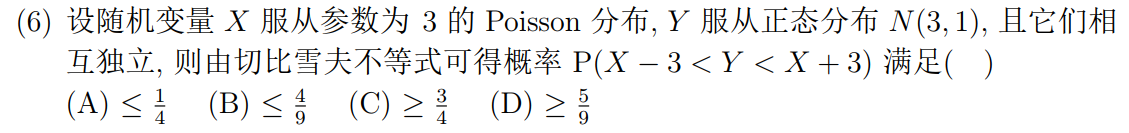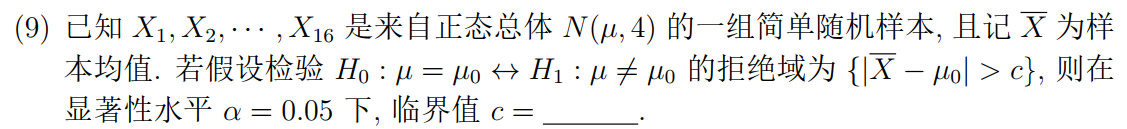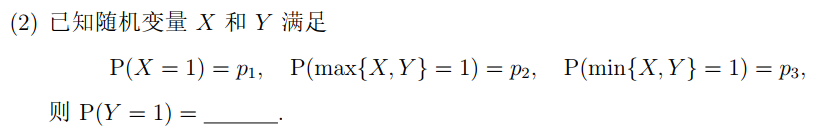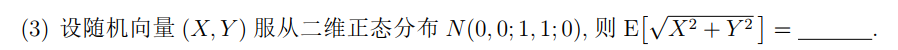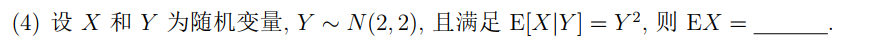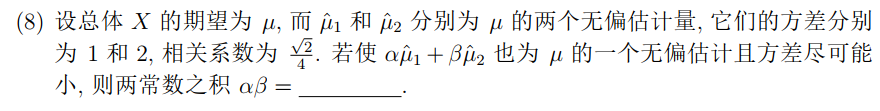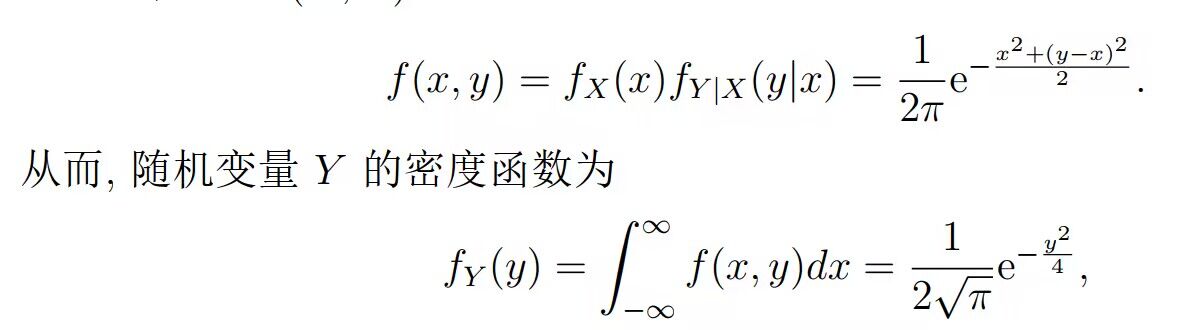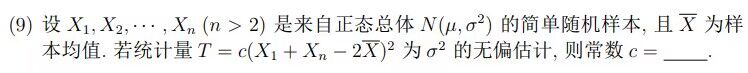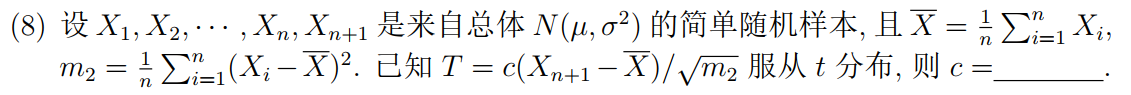几道题
写在前面
一些注意事项.
期望的线性性
不需要对 之间的关联附加任何限制关系,常用;
随机向量函数的期望
也是常用的,其中 为分布函数.
对求 的情形,理论上我们先通过随机向量函数的分布
求出 的分布,然后再通过期望的定义
求出 的期望,但这里的两次积分往往都比较复杂,尤其当分布比较难算的时候这个方法就不适用了. 这里就可以直接利用随机向量函数的期望直接求解.
如果二重积分比较困难,可以考虑积分换序. 例如,积分区域为 ,则
(2022 春 二.(3)).
有关 函数的一些公式:
. 特别地,
方差的计算:设 相互独立, 为 个常数,则
注意:当 相互独立时,!
有关 :
,则 ;
且 独立,则 .
有关 :
有关 :
;
.
抽样分布的其他结论:
题目解答
2022 秋

记 ,,则
所以

A:
B:例如取 ,则
C:若其为分布函数,则 为概率密度函数,但由 A 它不是;
D:验证:设 ,.
从而

一共可能有 个三角形.
记 第个三角形存在,则 .
即为三角形个数,.
上面的方法或许会有争议,其实这里可以直接用期望的可加性
求解.

A:因为 相互独立,所以有 .
容易验证 .
B:
C:
D:
若它们相互独立,记 .
即 是可分离变量的,从而 与 相互独立.

根据熵的定义
和 服从参数为 的指数分布,即
得
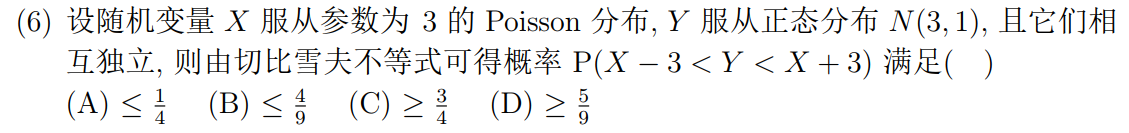
,则 ,.
取 ,则
其中方差的运算用到了 相互独立这一条件. 由切比雪夫不等式,
取 ,解得


由定义,A 正确; 值的定义与检验水平 无关,B 错误; 值与原假设 有关,C 错误;
D 还不确定.
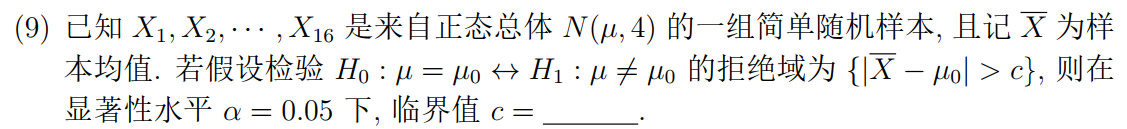
这是单个正态总体均值在方差已知情形下的第三个问题的检验.
当
时拒绝原假设,即临界值为 .

这是理论分布已知但含有有限个( 个,) 未知参数的拟合优度检验问题,取值有 个,则所求自由度为 .


(1)
其中区域 .
(2)
,则其概率密度函数为
分布函数为
同理,
的分布函数为
从而其概率密度函数为
的概率密度函数为
即
的分布函数为
从而其概率密度函数为
的概率密度函数为
即
证毕.
(3)
即 在 的条件下服从 上的均匀分布.
(4)
由
计算得
记 ,得
其中 是被 、、、 围起来的区域,. 计算得
期望
补充:这里应当直接考虑随机向量函数的期望进行计算:
所以,

(1)
(2)
由全概率公式,,
求导得
(3)
不会.

(1)
似然函数
解得
(2)
从而是无偏估计.
(3)
解不等式
得
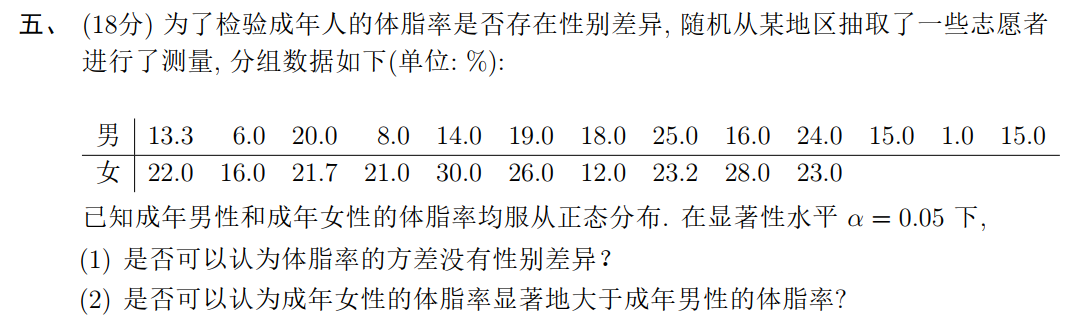
计算:记男性样本 ,女性样本 ,,则 ,则
(1)
这是两个正态总体方差比的检验,检验问题为
检验统计量为
其观测值为 .
临界值分别为 和 .
由于 ,接受 ,即可以认为体脂率的方差没有性别差异.
(2)
这是两个正态总体均值差的成组比较,检验问题为
由于方差未知,取检验统计量
其观测值为
临界值为 .
由于 ,拒绝 ,即可以认为成年女性体脂率显著大于成年男性体脂率.
2022 春

记 第次抛掷结果为正面,抛掷次硬币出现次正面,则
这相当于是抛掷硬币 次后有 次为正面、 次为反面,现从这 个结果中任选一个,求结果是正面的概率,那就是 . 这个结果应当是与抛掷硬币出现正面的概率无关的.
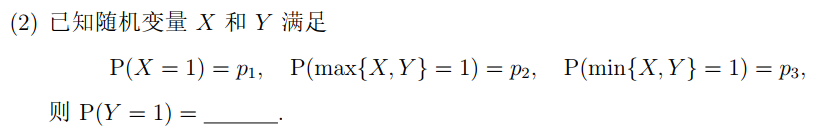
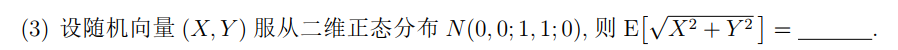
,则
期望为
利用随机向量函数的期望直接求解:
注:这里用到了
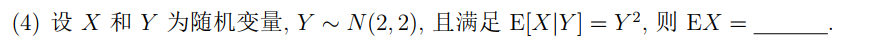
由全期望公式(平滑公式)得
又因为 ,得

设 ,事件 直线与边相交,则
而 服从 上的均匀分布,即
所以由全概率公式,

易知 ,从而
从而

A: 不服从 ;
B:,从而 ;另一方面,
但这两个随机变量不互相独立,所以它们的和不服从 ;
C:一眼错.
D:,记
则
且因为 和 相互独立,
和
也相互独立,从而根据 分布对自由度 的再生性,它们的和服从自由度为 的 分布.
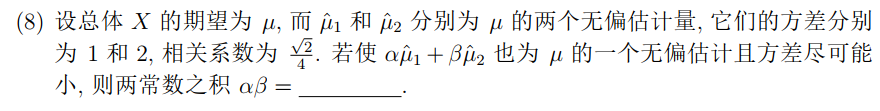
当且仅当 时等式成立. 此时 .

由于 ,有 ,A、B 正确,这从直观上也是容易看出的;
显然两者不等,C 错误;
D 正确.

显著性水平越小,原假设被保护得越好,从而更不容易被拒绝,所以 A 正确.

(1)
(2)
(3)
这里在一开始用到了积分换序的技巧.
(4)
综上,

(1)
,从而 .
区域 .
(2)
.
当 时, 的分布函数为
的概率密度函数为
当 时, 的分布函数为
的概率密度函数为
综上, 的概率密度函数为
(3)
判别式 ,即求 .

(1)
用 代替 、 代替 ,得
(2)
似然函数
因为 ,所以 ,因而 的最大似然估计 .
对数似然函数
(3)
的分布函数为
的分布函数为
期望为
修正值为
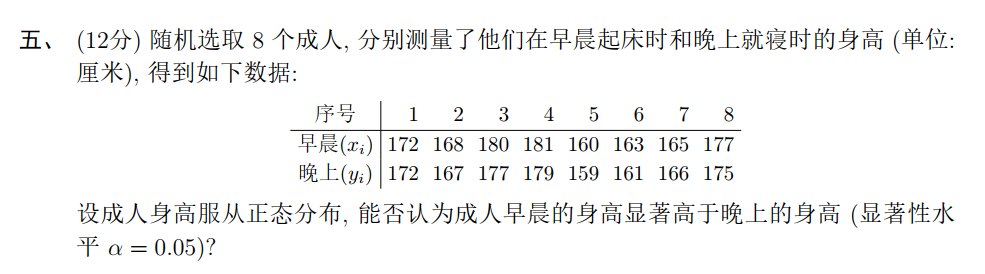
两个正态总体均值差的成对比较.
构造虚拟总体 .
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 早上 | 172 | 168 | 180 | 181 | 160 | 163 | 165 | 177 |
| 晚上 | 172 | 167 | 177 | 179 | 159 | 161 | 166 | 175 |
| 差 | 0 | 1 | 3 | 2 | 1 | 2 | -1 | 2 |
样本量 .
检验问题:.
检验统计量
则该检验问题的一个水平 的检验为:当 时拒绝 ,否则不能拒绝 .
的观测值为 ,临界值为 ,因为 ,所以拒绝 ,即可以认为成人早晨的身高显著高于晚上的身高.
其他
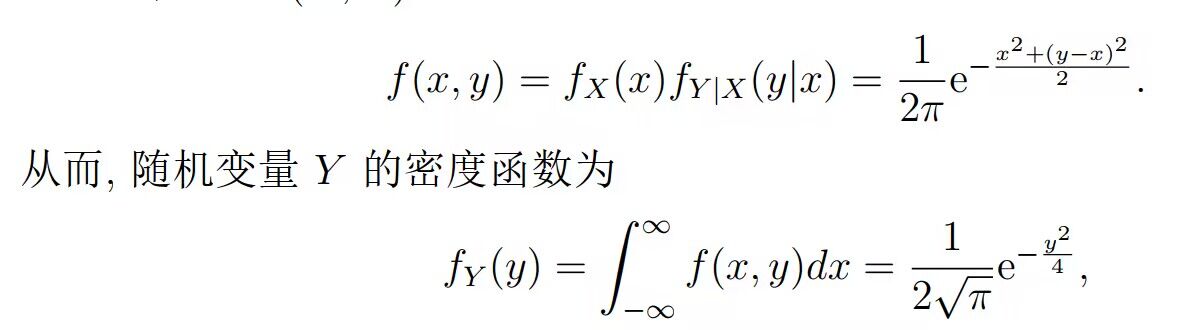

记 随机抽取台均为一等品,取划分 售出一台一等品,售出一台二等品,则
由贝叶斯公式,
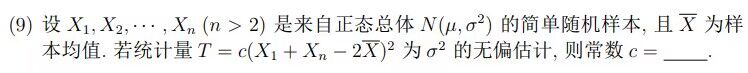
令
则
从而,
,,从而 ;
,则
;
因为
所以
其中 ,故 ;,所以有
同理,也有
综上,有

从形式上看,随机变量
可能服从 分布,下面分别验证关于 和 的分布.
因为 ,有 ,,从而
这里用到了:
独立同分布的随机正态变量的线性组合服从正态分布,
及样本均值
原式
又因为
这是因为
且这里 和 是相互独立的,
这是因为样本均值 和样本方差 是相互独立的.
容易知道 和 也是相互独立的,从而得到 服从自由度为 的 分布,即
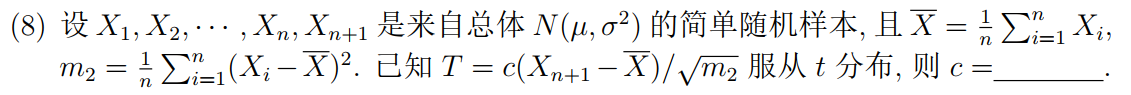
由 ,得
又由 ,得
所以
另一方面,
而
故