数理逻辑基础
HW1
题目1

(1)
| | | | |
|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
该式为永假公式(矛盾式).
(2)
| | | | | | |
|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
该式为永真公式(重言式).
(3)
| | | | | |
|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
该式为可满足公式.
题目2

| | | | | | | | | |
|---|
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
从而公式 和 适合德·摩根律
题目3
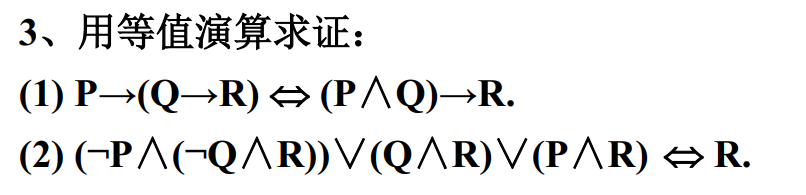
(1)
(2)
在上的分配律的交换律 由 ,,
的结合律、式在上的分配律排中律幺律 HW2
题目1

(1)
蕴涵等值式蕴涵等值式的结合律德摩根定律德摩根定律 (2)
蕴涵等值式德摩根定律在上的分配律双重否定律德摩根定律德摩根定律 (3)
等价等值式蕴涵等值式在上的分配律在上的分配律矛盾律幺律的交换律双重否定律德摩根定律 题目2

(1)
中结果德摩根定律 (2)
中结果 (3)
双重否定律德摩根定律 式双重否定律 从而,
中结果式、 题目3

(1)
蕴涵等值式蕴涵等值式双重否定式德摩根定律的结合律吸收律的交换律 即原公式的析取范式是 . 同时它也是合取范式.
(2)
德摩根定律、双重否定式的交换律 即原公式的合取范式是 ,同时它也是析取范式.
(3)
蕴涵等值式德摩根定律、的结合律德摩根定律在上的分配律幺律、排中律在上的分配律在上的分配律、的交换律与结合律排中律、吸收律幺律、的幂等律 即原公式的析取范式是 或 ,
合取范式是 .
HW3
题目1

(1)
| | | | |
|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
主析取范式为
主合取范式为
(2)
| | | | |
|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
主析取范式为
主合取范式为 .
(3)
| | | | | |
|---|
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
主析取范式为 ,主合取范式为
题目2

主析取范式为
主合取范式为
题目3

主合取范式为
主析取范式为
HW4
题目1

(1)
幺律排中律分配律 幺律排中律分配律幺律排中律分配律分配律 替换定理、的幂等律 (2)
蕴涵等值式分配律矛盾律幺律幺律排中律分配律的幂等律 题目2

蕴涵等值式分配律、交换律的幂等律吸收律吸收律幺律排中律分配律吸收律幺律、排中律分配律 蕴涵等值式 题目3

所求公式 ,其中 ,,.
蕴涵等值式 蕴涵等值式双重否定律、交换律 从而
替换定理分配律、交换律矛盾律幺律分配律矛盾律、的幂等律零律幺律幺律排中律分配律
| | | | | | | | | |
|---|
| 0 | 0 | 0 | 0 | 0 | 1 | | | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | | | | |
| 2 | 0 | 1 | 0 | 1 | 1 | | | | |
| 3 | 0 | 1 | 1 | 1 | 0 | | 0 | | 0 |
| 4 | 1 | 0 | 0 | 1 | 1 | 0 | | | 0 |
| 5 | 1 | 0 | 1 | 1 | 0 | | | | |
| 6 | 1 | 1 | 0 | 1 | 1 | 0 | | | 0 |
| 7 | 1 | 1 | 1 | 1 | 0 | | 0 | | 0 |
派遣方案:
A、B 不去,C 去;
A、C 不去,B 去;
B 不去,A、C 去.
HW5
题目1

记
:早饭吃面包;
:早饭吃蛋糕;
:早饭喝牛奶;
:早饭喝咖啡.
前提: ,,,,
结论:.
推理:
(前提引入)
(前提引入)
(1, 2 拒取式)
(前提引入)
(3, 4 析取三段论)
(前提引入)
(5, 6 假言推理)
(5, 7 合取引入)
题目2

根据 CP 规则,只需要从前提 推理出 即可.
推理:
(前提引入)
(附加前提引入)
(1, 2 析取三段论)
(前提引入)
(3, 4 假言推理)
(前提引入)
(5, 6 假言推理)
从而有 .
题目3

记
:国际米兰夺冠
:AC 米兰获亚军
:尤文图斯获亚军
:拉齐奥获亚军
前提: ,,,.
结论:.
推理:
(前提引入)
(前提引入)
(1, 2 假言推理)
(前提引入)
(2, 4 拒取式)
(3, 5 析取三段论)
(前提引入)
(6, 7 拒取式)
(结论的否定,附加前提引入)
(合取引入)
10 为一个矛盾式,故根据归谬法,原结论成立,论述有效.
HW6
题目1

题目2

(1)
,证明 .
(假定)
(换位律)
(1, 2 MP)
(2)
,证明 .
由演绎定理,只需要证明 .
(否定前件律)
(假定)
(1, 2 MP)
(L1)
(新假定)
(4, 5 MP)
(3, 6 MP)
(3)
,证明 .
(假定)
(假定)
(1, 2 MP)
(1, 3 MP)
(4)
,证明 .
由演绎定理,只需要证明 .
又由反证律,只需要证明 且 即可.
一方面,
(假定)
(换位律)
(1, 2 MP)
(反证律-新假定)
(3, 4 MP)
另一方面,
(演绎定理-新假定)
(换位律)
(1, 2 MP)
(反证律-新假定)
故根据反证律,有 ,再根据演绎定理有 .
题目3

归谬律: 且 .
反证律: 且 .
已知 是从 的证明,即
...
// 从 的证明
(新假定)
(, MP)
将引入的 替换为 ,再根据双重否定律,改写如下:
...
// 从 的证明
(新假定)
(双重否定律)
(, MP)
(, MP)
从而,我们得到 是从 的证明.
同理可证, 是从 的证明.
根据归谬律,知 是从 的证明,即
...
(双重否定律)
(, MP)
(双重否定律)
(, MP)
即 是从 的证明.
HW7
题目1
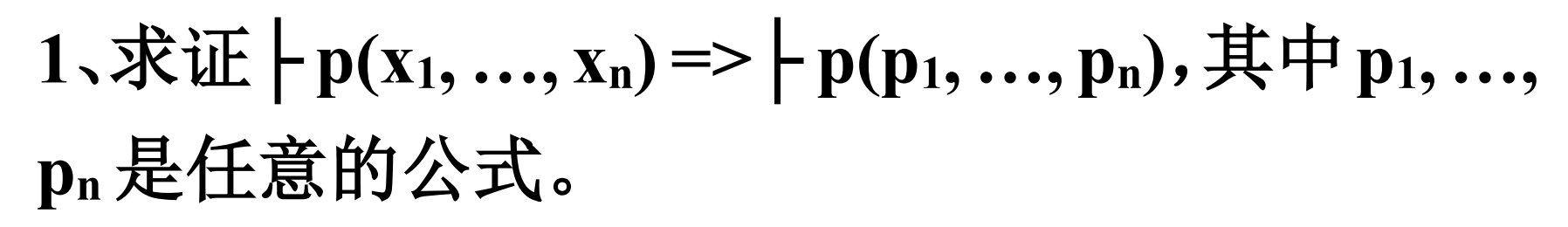
证明:
由语法推论的定义,因为 ,即 是 的公理,故 . 从而,对任意公式集 ,都有 .
又由命题演算 的可靠性,. 特别,取 ,则 .
根据语义推论的定义,此时有 ,即 永真. 取 ,则 .
对任意公式集 ,因为永真公式都是 的语义推论,有 .
由命题演算 的完备性,有 . 特别,取 ,则 .
根据语法推论的定义, 是 的定理,即 .
题目2

证明:
由命题演算 的完备性,有 .
综上,一定有 的有限子集 使得 .
由命题演算 的可靠性,有 .