经典一维随机游走
点击下载pdf
一、背景
>>1827 年,苏格兰植物学家罗伯特·布朗发现水中的花粉及其它悬浮的微小颗粒不停地作不规则的
曲线运动,称为布朗运动。人们长期都不知道其中的原理。50 年后,J·德耳索提出这些微小颗粒是受 到周围分子的不平衡的碰撞而导致的运动。后来得到爱因斯坦的研究的证明。布朗运动也就成为分子 运动论和统计力学发展的基础。爱因斯坦在研究布朗运动的原理过程中,根据分子热运动的原理,利用一维随机走动模型,得到了在一定时间内微粒在某一方向上位移的统计平均值[1]。
>>随机走动模型被用作物理布朗运动和扩散的简化模型,以一维固定步长随机游走为例,通常粒子
的每次位移都与之前的位移无关,这实际上是一个特殊的马尔可夫链过程。在课堂上我们通过组合数 的办法求出了一维随机走动模型的显示解,在这里我尝试用马尔科夫链模型的方式来分析这个过程。
二、分析
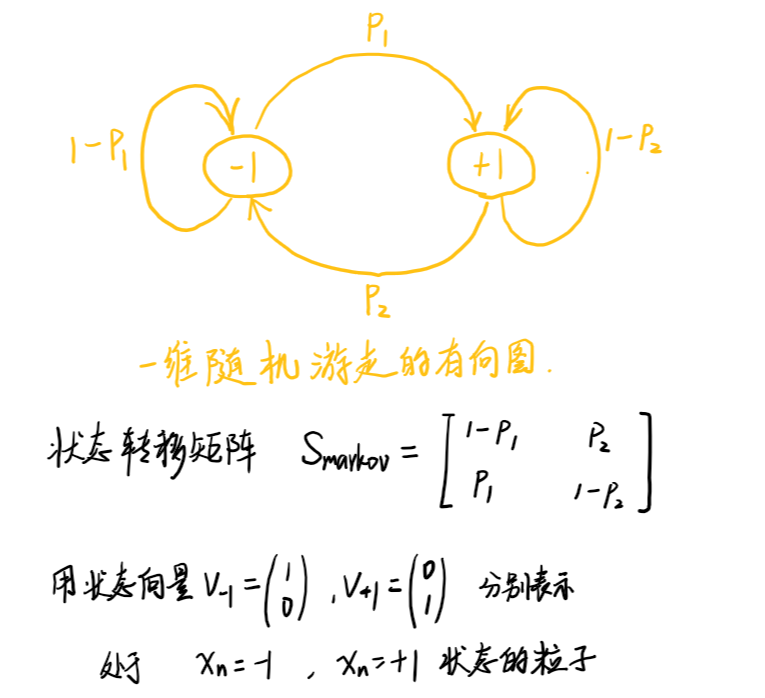
>>最简单的,我们可以考虑一个一维的,步长固定的离散时间随机行走模型。当粒子从原点出发
时,它有1-p 的概率往左运动,有p 的概率往右运动,每次运动的步长为 1。下一时刻也是如此。
>>对于一个总共 N 步的过程,粒子从x=0 位置出发,粒子处于可能有m=2N+1 个状态,分别为
S1、S2、…S2N+1分别对应x=-N,-N+1,…N。
>>在 n 时刻,粒子的位置可以表示为Tn= x0+x1+…xn,其中xi (i=1,2,…,n)为对应每一次移动的随机变
量,P(xi=1)=p, P(xi=-1)=1-p, x0 是粒子的处于初始位置,故x0=1。
>> 令 pij 为粒子从Sj 移动到Si 的概率,可以得到转移矩阵P=(pij)m×m,
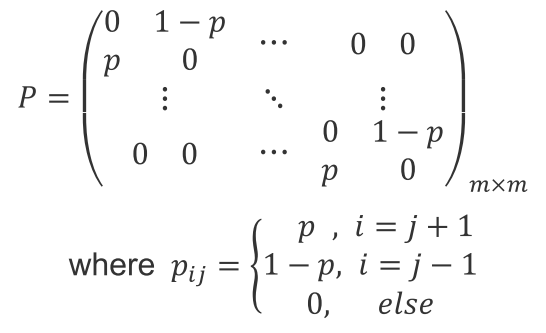
>>转移矩阵描述了粒子的运动方式和边界条件,比如在pk,(k+1)=0,pk-1,k=1,k<N 时,就描述了一个
位于原点右侧的反射边界。
考虑粒子从原点出发,p=0.5,因此T0=(0…0 1 0…0)T, T1=(0…0 1/2 0 1/2 0…0)T,递推公式Tn+1=
PTn,最终可以得到Tn = PnT0。
>>TN 是一个m维的列向量,含义即为N步之后粒子处于各个位置的概率分布。
>>以上是利用马尔可夫链模型的方法对随机游走模型进行分析,通过对转移矩阵的n 次方进行计算,可以得到任意n 时刻的概率分布。
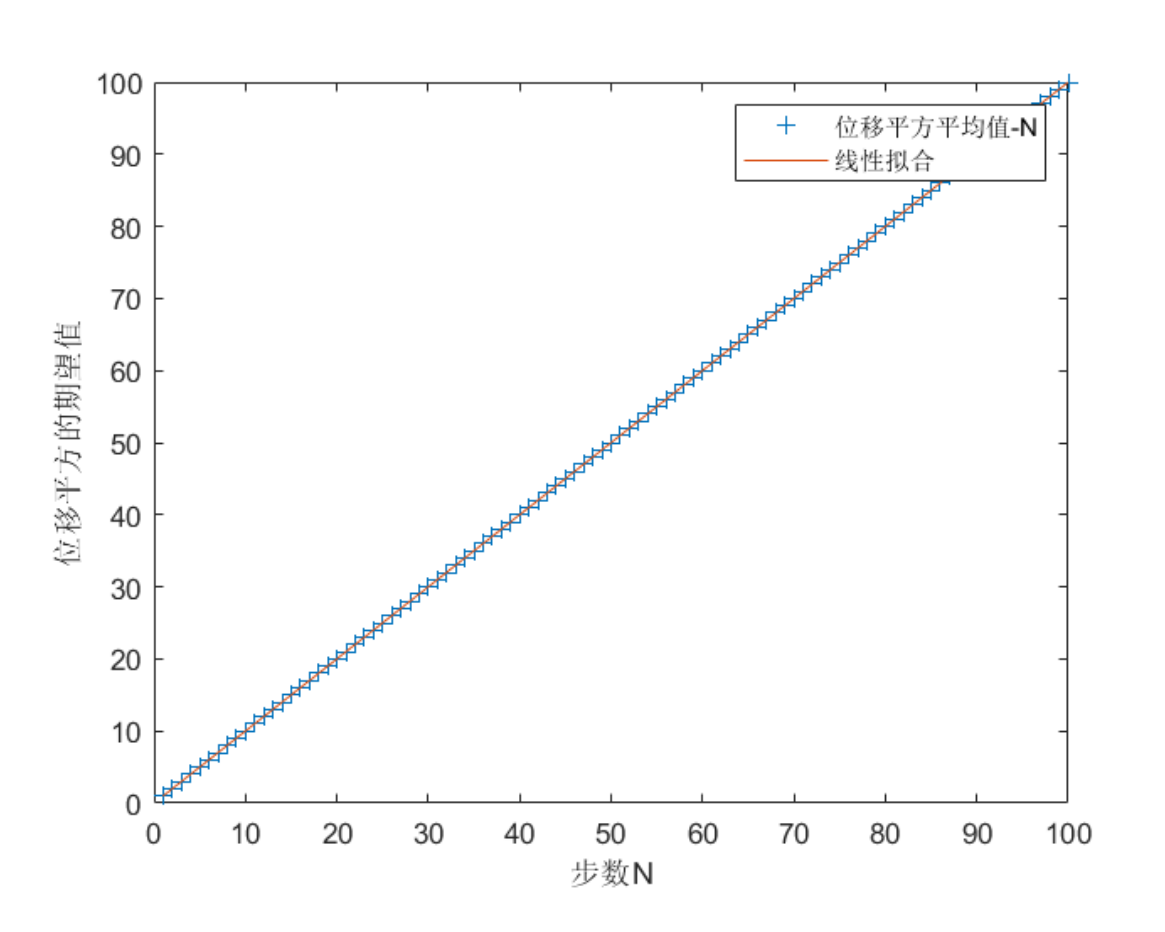
>>下面是按照以上计算得到的“位移平方的期望值”随步数N的变化,可以得到√(x2)∝ √N,与课堂中得到
的结果相同。
三、总结
>>用马尔可夫链模型的方法分析了一维随机游走模型,并进行了验证性的计算,得到√x2 ∝ √N与课堂中
相同的结果。其中,得到的转移矩阵P 对于各种情况都可以比较方便的构造以满足特定的运动方式和边界条件,因此这种分析方法更容易向更复杂的情况推广。
参考文献
[1]百度百科-布朗运动
[2]知乎-马尔科夫链与随机游走问题