Deutsch Jozsa算法
Latest editation: 2022年3月6日 20点34分
Deutsch-Jozsa算法是最经典的量子算法之一,解决的是判断函数类型的问题,证明量子计算在解决某些问题时具有指数加速的能力。 1992 年由David Deutsch 和 Richard Jozsa提出了第一个量子算法Deutsch-Jozsa 量子算法, 简称D-J 算法,这是第一个展示了量子计算和经典计算在解决具体问题时所具有明显差异性的算法。

Question
已知函数 f: {0,1}⊗n(⊗n) → {0,1}一定是下列两种形式的一种
(1)constant: ∀x, f(x)=0 or ∀x, f(x)=1
(2)balanced: f(x)=0 for half of {0,1}⊗n and f(x)=1 for the other half
问如何用最少的查询次数确定f属于二者中的哪一种?
Deutsch-Jozsa算法
Input: black box oracle Uf |x⟩ |y⟩=|x⟩ |y ⊕ f(x)⟩
Output: f is constant or balanced
Steps:
1. |0⟩⊗n|1⟩上作用Hadamard门 H⊗(n+1)变为态 |+⟩⊗n |-⟩
2. 作用oracle Uf
3. 在工作位作用 H⊗n后进行测量
4. 如果结果为 |0⟩⊗n的概率为1,则 f is constant; 概率为0则 f is balanced
where |+⟩=(|0⟩+|1⟩)/√2 |+⟩=(|0⟩-|1⟩)/√2
DJ算法的量子线路
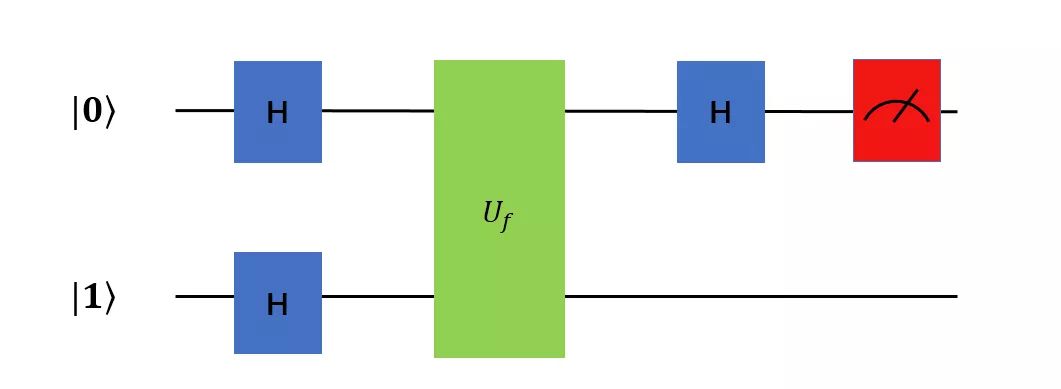
Proof
初态:φ0=|0⟩⊗n|1⟩
作用Hadamard算子后得到φ1

(可通过抛硬币n次直观理解)
作用oracle Uf后得到φ2

忽略低位的辅助比特 (|0⟩-|1⟩)/√2
怎么计算 H⊗n|x⟩ ? 我们从这里出发:


于是我们知道:

如果是多个比特呢?比如从两个比特开始:

如果是n位的话,就是

我们x表示x1,x2,...xn我们z表示z1,z2,...zn,设定格式x⋅z表示x1⋅z1+x2⋅z2...xn⋅zn,那么就有:

所以

最后对工作位Qubit进行测量,我们关注|z⟩=|0⟩⊗n的概率 P0
也就是系数的平方:

若 f(X) is constant, 我们将得到 P0=1;
若 f(X) is balanced, 我们将得到 P0=0。
在整个过程中,oracle我们只查询了一次。
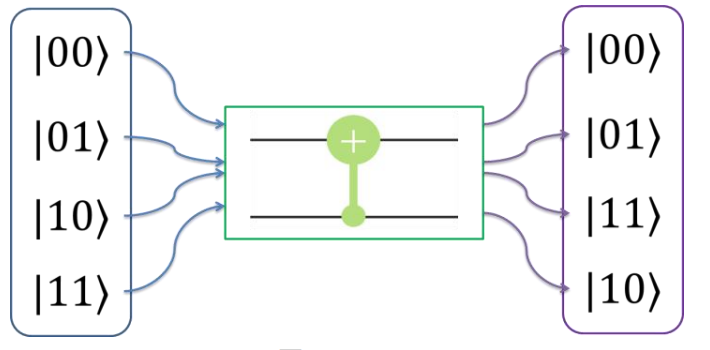
CNOT门作为oracle的验证
以高位控制的CNOT门为例,如图所示的输出结果可以看到,f(0)=0,f(1)=1,CNOT门作为oracle其中的function f(x) is balanced
>基于本源量子云的全振幅量子虚拟机,绘制量子线路,预测测量的结果应该为,P(1)=1,P(0)=0

测量结果为:
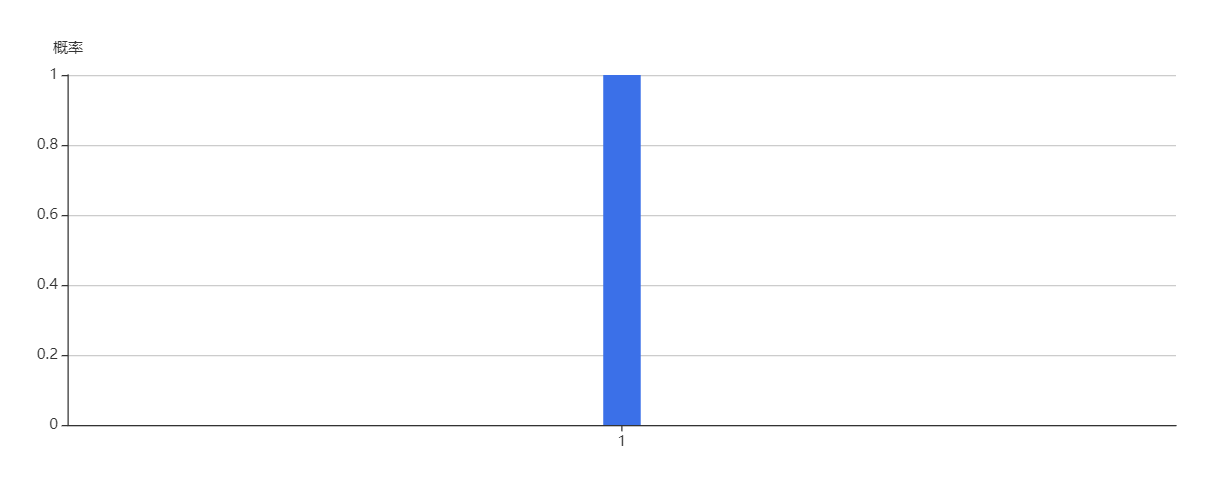
f is balanced
Questions left
DJ算法为我们展示了量子算法相较于经典算法的优势和可能性,这种相干的思想,类似于双缝干涉实验最开始为人们带来的启发性。如何将这样的思想进行推广?是否通过oracle的精心设计,可以达到一些令人惊喜的效果?
References
[1]【科普】量子计算通识-8-Deutsch-Jozsa算法解析 - 简书 (jianshu.com) [2]【科普】量子计算通识-7-Deutsch算法解析 - 简书 (jianshu.com) [3]金刚石量子计算体系简述6:Deutsch-Jozsa算法 - 知乎 (zhihu.com) [4]Deutsch-Jozsa 算法 简述 - 知乎 (zhihu.com) [5]《量子计算与编程入门》郭国平,陈昭昀,郭光灿著,科学出版社