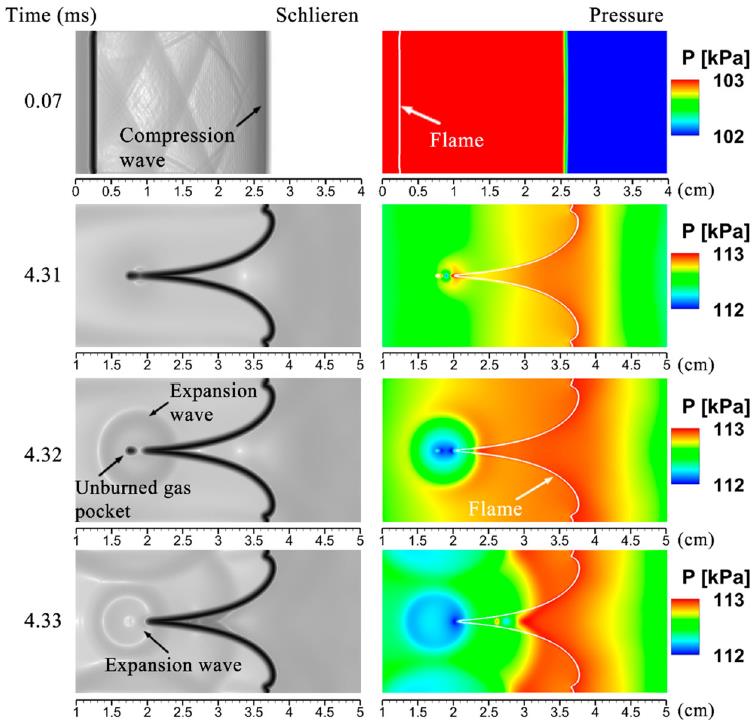
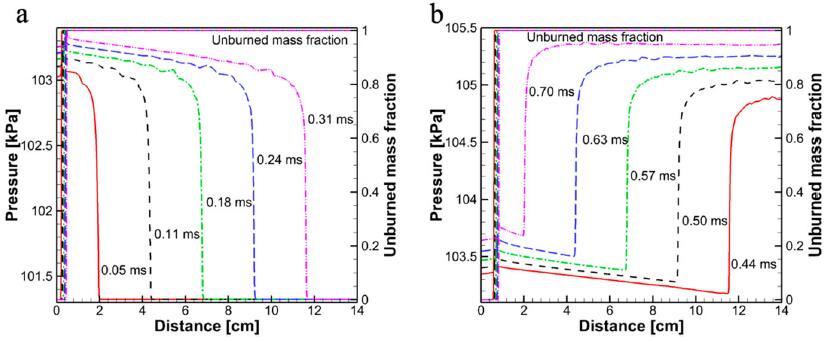
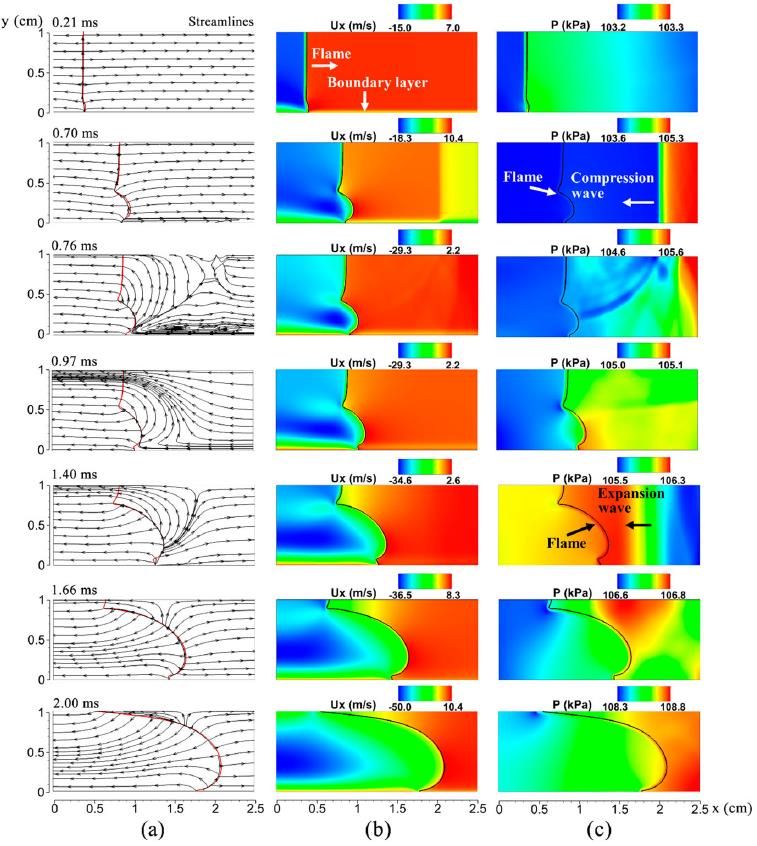
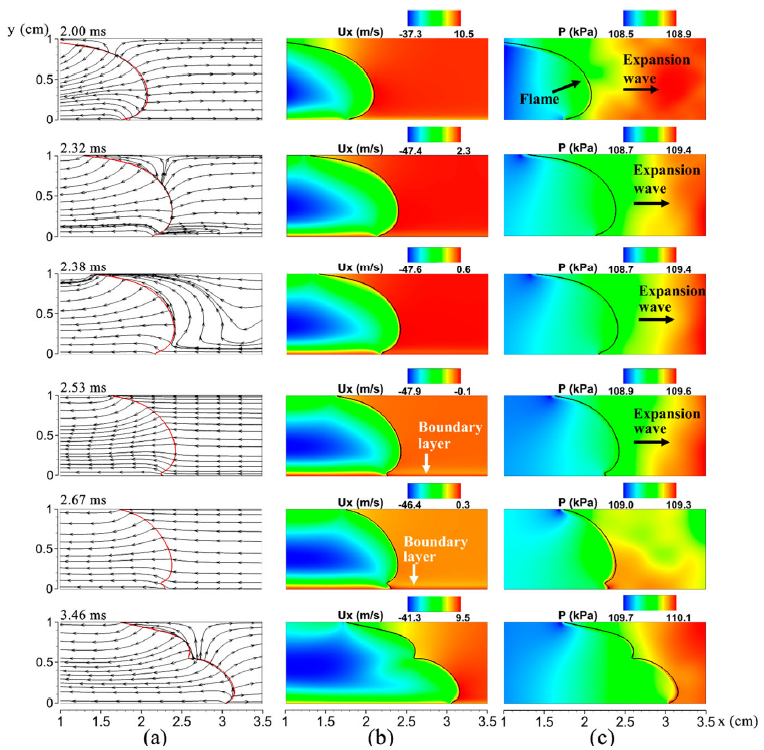
Numerical study of the stability of premixed flames propagating in half-open tubes
Ting Shen, Huahua Xiao*
简介:
通过运用高精度算法结合动态自适应网格技术求解二维全可压的反应性Navier-Stokes方程,以研究半开口管道内预混火焰的传播动力学。利用简化的化学-扩散模型(CDM)描述当量比的氢-空气混合物中的化学反应和扩散过程。通过固定管道长宽比a = 7,改变管道长度以研究管道尺寸对火焰传播动力学和火焰变形的影响机制。数值结果表明,在本文考虑的所有尺寸的管道内,经开口端点火后,火焰都能演化成郁金香火焰(TF)。管道尺寸的变化引起TF的进一步演变和膨胀波放的形成产生差异。在较大尺寸的管道(管道高度d > 0.5 cm)中,TF进一步发展为一系列更不稳定的变形郁金香火焰(DTFs)。相比之下,在较小尺寸的管道中(d < 0.5 cm)中,TF的形状一直保持到燃烧结束。此外,在大尺寸管道内火焰传播的整个过程中,火焰和压力几乎都发生了明显的振荡,而在小尺寸管道中,TF形成后的火焰和压力的振荡行为可以忽略不计。研究发现,对于相同长宽比的半开口管道,TF的形成机制因管道尺寸变化而不同。通过进一步分析火焰、边界层和压力波之间的相互作用,总结了半开口管道内TF形成的两种机制:(1) 在较大管道 (d ≥ 0.5 cm)中主要由于边界层作用,(2) 在最小管道(d = 0.25 cm)中,主要由于压缩波驱动的火焰面的Rayleigh-Taylor不稳定性。半开管内DTF的形成与TF尖端崩塌过程中产生的膨胀波密切相关,膨胀波在火焰前沿前的壁面边界层中引起反向流动,从而引发DTF。
Abstract:
This paper studies premixed flame dynamics in half-open tubes by solving the twodimensional, fully compressible, reactive Navier-Stokes equations on a dynamically adapting mesh using a high-order algorithm. A simplified chemical-diffusive model was used to describe the chemical reaction and diffusive transports in a stoichiometric hydrogen-air mixture. The influence of the length scale was examined by considering four tube heights at a fixed aspect ratio a = 7. The numerical simulations show that the flame evolves into a tulip flame (TF) in all the tubes shortly after being ignited at the open end. Variation in tube size leads to differences in the evolution of TF and generation of expansion waves. In a sufficiently large tube (d > 0.5 cm), the TF further develops into a series of more unstable distorted tulip flames (DTFs). By contrast, in a small tube (d < 0.5 cm), the TF shape remains until the end of the combustion. In addition, both the flame and pressure oscillate significantly almost in the entire process of flame propagation in the large tubes, while the oscillating behaviour in flame or pressure is negligible in the small tube after TF forms. It was found that the TF formation mechanism is length-scale dependent even for the same type of geometry and condition. A detailed examination of the interactions between flame, boundary layer, and pressure waves showed two mechanisms of TF formation: (1) boundary layer effect for the larger tubes (d ≥ 0.5 cm), and (2) Rayleigh-Taylor instability driven by compression waves for the smallest tube (d = 0.25 cm). The DTF formation in the half-open tubes is closely related to the expansion waves generated by the collapse of the TF cusp. The expansion waves cause a reverse flow in the boundary layer ahead of the flame front and consequently initiate the DTF.
Figures: