补充材料-数值求根算法

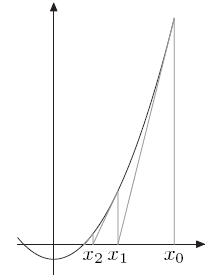
首先，选择一个接近函数$f(x)$零点的$x_{0}$，计算相应的$f(x_0)$和切线斜率$f'(x_0)$（这里$f'$表示函数$f$的导数）。然后我们计算穿过点$(x_{0},f(x_{0}))$并且斜率为$f'(x_0)$的直线和$x$轴的交点的$x$坐标，也就是求如下方程的解：

$0=(x-x_{0})\cdot f'(x_{0})+f(x_{0})$

我们将新求得的点的$x$坐标命名为$x_1$，通常$x_1$会比$x_{0}$更接近方程$f(x)=0$的解。因此我们现在可以利用$x_1$开始下一轮迭代。迭代公式可化简为如下所示：

$x_{{n+1}}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}$

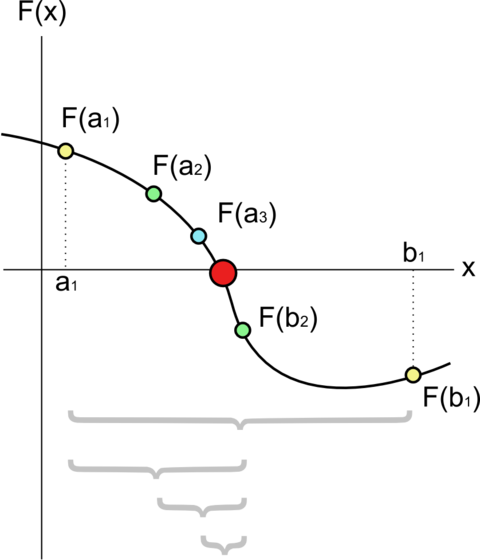
若要求已知连续函数$f(x)=0$的根($x$的解)，则:

1. 先找出一个区间$[a, b]$，使得$f(a)$与$f(b)$异号。根据介值定理，这个区间内一定包含着方程式的根
2. 求该区间的中点$m={\frac {a+b}{2}}$，并找出$f(m)$的值
3. 若$f(m)$与$f(a)$正负号相同则取$[m, b]$为新的区间, 否则取$[a, m]$
4. 重复第2和第3步至理想精确度为止