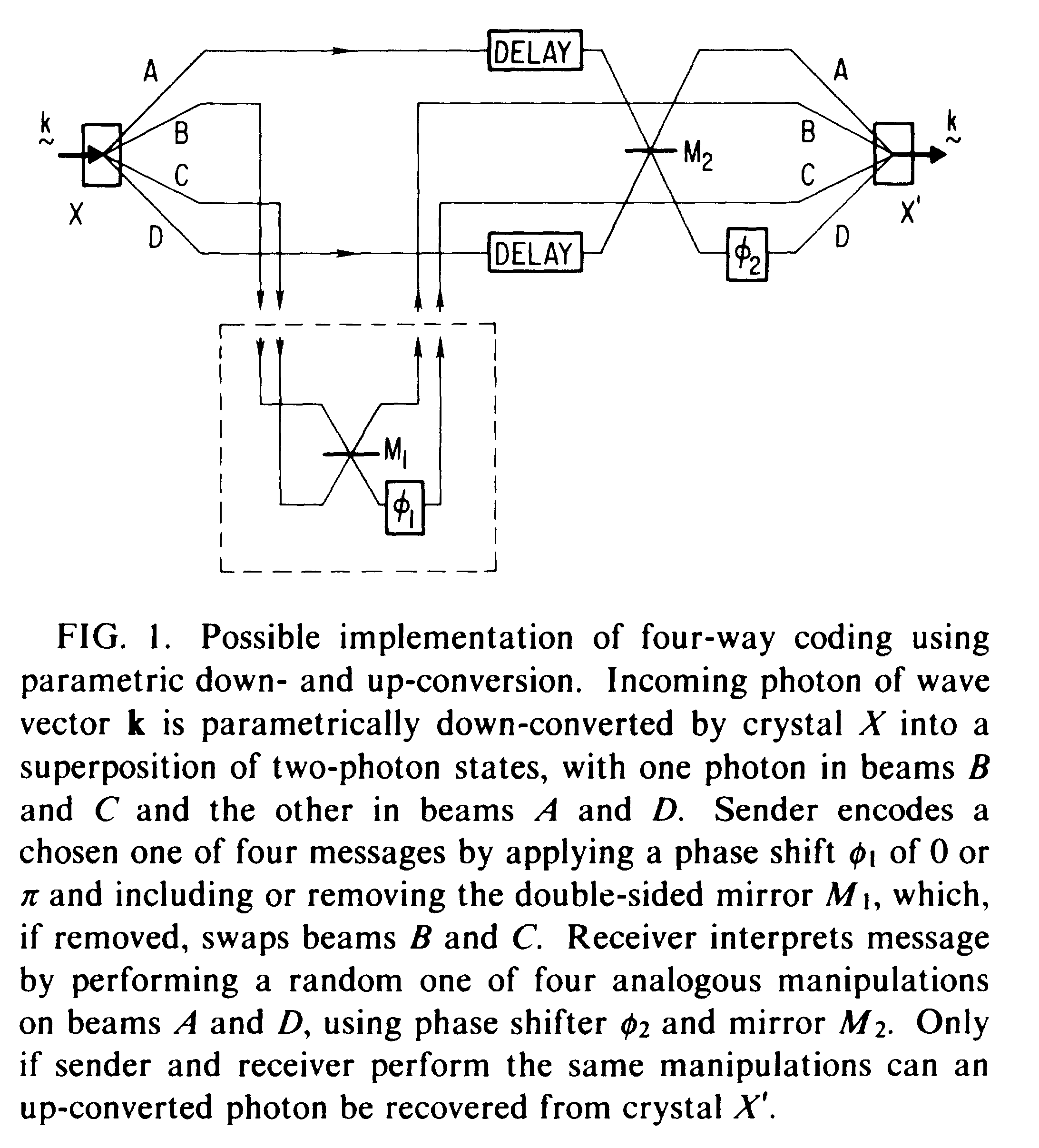
1.7.1. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states[18]
As is well known, operations on one particle of an Einstein-Podolsky-Rosen (EPR) pair cannot influence the marginal statistics of measurements on the other particle. We characterize the set of states accessible from an initial EPR state by one-particle operations and show that in a sense they allow two bits to be encoded reliably in one spin particle: One party, “Alice,” prepares an EPR pair and sends one of the particles to another party, “Bob,” who applies one of four unitary operators to the particle, and then returns it to Alice. By measuring the two particles jointly, Alice can now reliably learn which operator Bob used.
We show that such interactions can be used to prepare all and only those states of the joint system (two particles and ancilla) that yield unperturbed marginal statistics for all measurements on the other particle, with which the ancilla did not interact.
We now demonstrate the equivalence between states accessible through one-particle operators and states with random marginal statistics for the untreated particle. A general expression for a pure state of the tripartite system comprising the two EPR particles and the ancilla is
The symmetry of Eqs. (1) and (2) with respect to the coefficients of and implies that unitary operations on one particle of an EPR pair, without ancilla, cannot influence the marginal statistics of either particle, not even the one the operator has acted upon.
It is noteworthy that the manifold defined by Eqs. (1) and (2), i.e., the set of states preparable by one-particle unitary operators on an initial EPR state, is a proper subset, but not a subspace, of all two-particle pure states. It includes states such as
The orthonormality of Eq. (3) means that manipulations of one particle of a separated EPR pair, while they cannot be used to communicate directly with the untreated particle, can be used to encode four reliably distinguishable messages in the two-particle system. To perform this feat, Alice, the intended receiver of the message, first prepares a pure EPR state and lends one particle of the pair to Bob, the intended sender. Bob then operates on the particle via one of four unitary operators so as to put the two-particle system into a chosen one of the four states of Eq. (3) and then returns the treated particle to Alice. Now possessing both particles, Alice can in principle measure them jointly in the orthonormal basis of Eq. (3), and so reliably learn which operator Bob applied.
From one viewpoint, this is surprising, because Bob has communicated a two-bit message by unitarily operating on a single spin particle. Thinking too classically, one might be tempted to say that his manipulations have therefore placed the treated particle into four reliably distinguishable states, contradicting a basic principle of quantum mechanics that such a particle can have only two reliably distinguishable states. But the scheme also depends on the untreated particle. It therefore might be better to say, as Schumacher suggests, that one of the two bits is sent forward in time through the treated particle, while the other bit is sent backward in time to the EPR source, then forward in time through the untreated particle, until finally it is combined with the bit in the treated particle to reconstitute the two-bit message. Because the bit “sent backward in time” cannot be used to transmit a meaningful message without the help of the other particle, no opportunity for time travel or superluminal communication is created, just as none is created in the classic EPR experiment in which simultaneous measurements are used to establish non-message-bearing correlations over a spacelike interval.
The EPR scheme has the advantage of allowing some of
the particle transmissions to take place before the message has been decided upon, perhaps at cheaper “off-peak” rates.