1.5.4. Observation of Three-Photon Greenberger-Horne-Zeilinger Entanglement [15]
We present the experimental observation of polarization entanglement for three spatially separated photons. Such states of more than two entangled particles, known as Greenberger-Horne-Zeilinger (GHZ) states, play a crucial role in fundamental tests of quantum mechanics versus local realism and in many quantum information and quantum computation schemes. Our experimental arrangement is such that we start with two pairs of entangled photons and register the photons in a way that any information as to which pair each photon belongs to is erased. After detecting a trigger photon, the registered events at the detectors for the remaining three photons exhibit the desired GHZ correlations.
The main idea is to transform two pairs of polarization entangled photons into three entangled photons and a fourth independent photon. In our experiment the GHZ entanglement is observed only under the condition that both the trigger photon and the three entangled photons are actually detected. Thus, detection plays the double role of both projecting into the GHZ state and performing a specific measurement on the state.
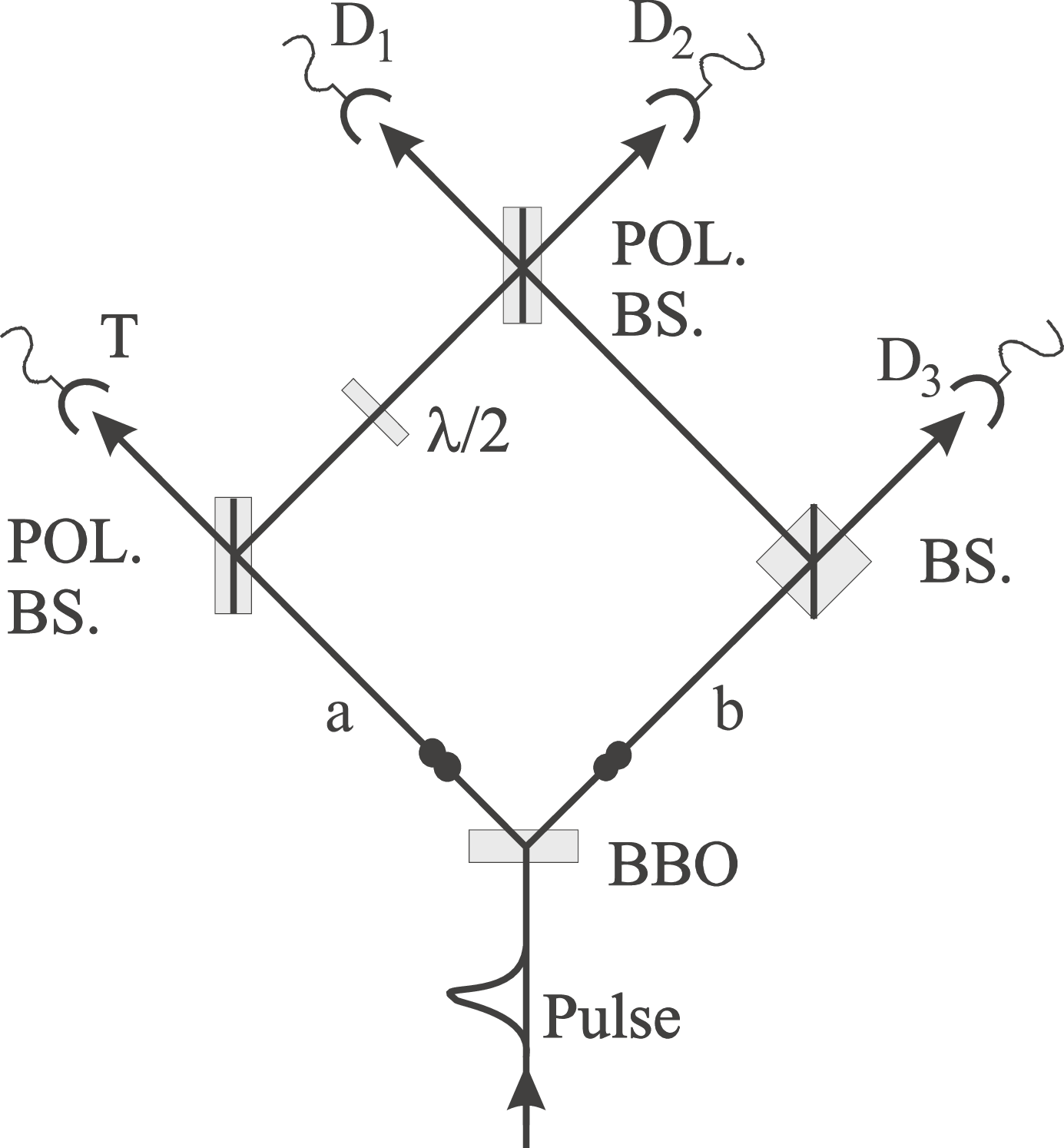
FIG. 1. Schematic drawing of the experimental setup for the demonstration of the Greenberger-Horne-Zeilinger entanglement for spatially separated photons. Conditioned on the registration of one photon at the trigger detector T, the three photons registered at and exhibit the desired GHZ correlations.
The pair creation is such that the following polarization entangled state is obtained: The setup is such that arm a continues towards a polarizing beam splitter, where V photons are reflected and H photons are transmitted towards detector T (behind an interference filter 4.6 nm at 788 nm). Arm b continues towards a 50y50 polarization-independent beam splitter. From each beam splitter, one output is directed to a final polarizing beam splitter. In between the two polarizing beam splitters, vertical polarization is rotated to polarization using a plate. The remaining three output arms continue through interference filters ( 3.6 nm) and single-mode fibers towards the single-photon detectors and .
Consider two down-conversions producing the product state Initially, we assume that the components and created in one down-conversion might be distinguishable from the components and created in the other one. The evolution of the individual components of state (5) through the apparatus towards the detectors and is given by Inserting these expressions into state (1) and restricting ourselves to those terms where only one photon is found in each output we obtain, after normalization, If now the experiment is performed such that the photon states from the two down-conversions are indistinguishable, we finally obtain the desired state To experimentally demonstrate that GHZ entanglement has been obtained by the method described above,we first verified that, conditioned on a photon detection by the trigger T, both the and the components can be observed, but no others. Existence of the two terms as just demonstrated is a necessary but not yet sufficient condition for demonstrating GHZ entanglement. In fact, there could, in principle, be just a statistical mixture of those two states. Therefore, one has to prove that the two terms coherently superpose. This we did by a measurement of linear polarization of photon 1 along , bisecting the H and V directions.
For an additional confirmation of state (2) we performed measurements conditioned on the detection of
the photon at under polarization(i.e., V polarization). For the GHZ state this implies that the remaining two photons should be in the state which cannot give rise to any correlation between these two photons in the detection basis.
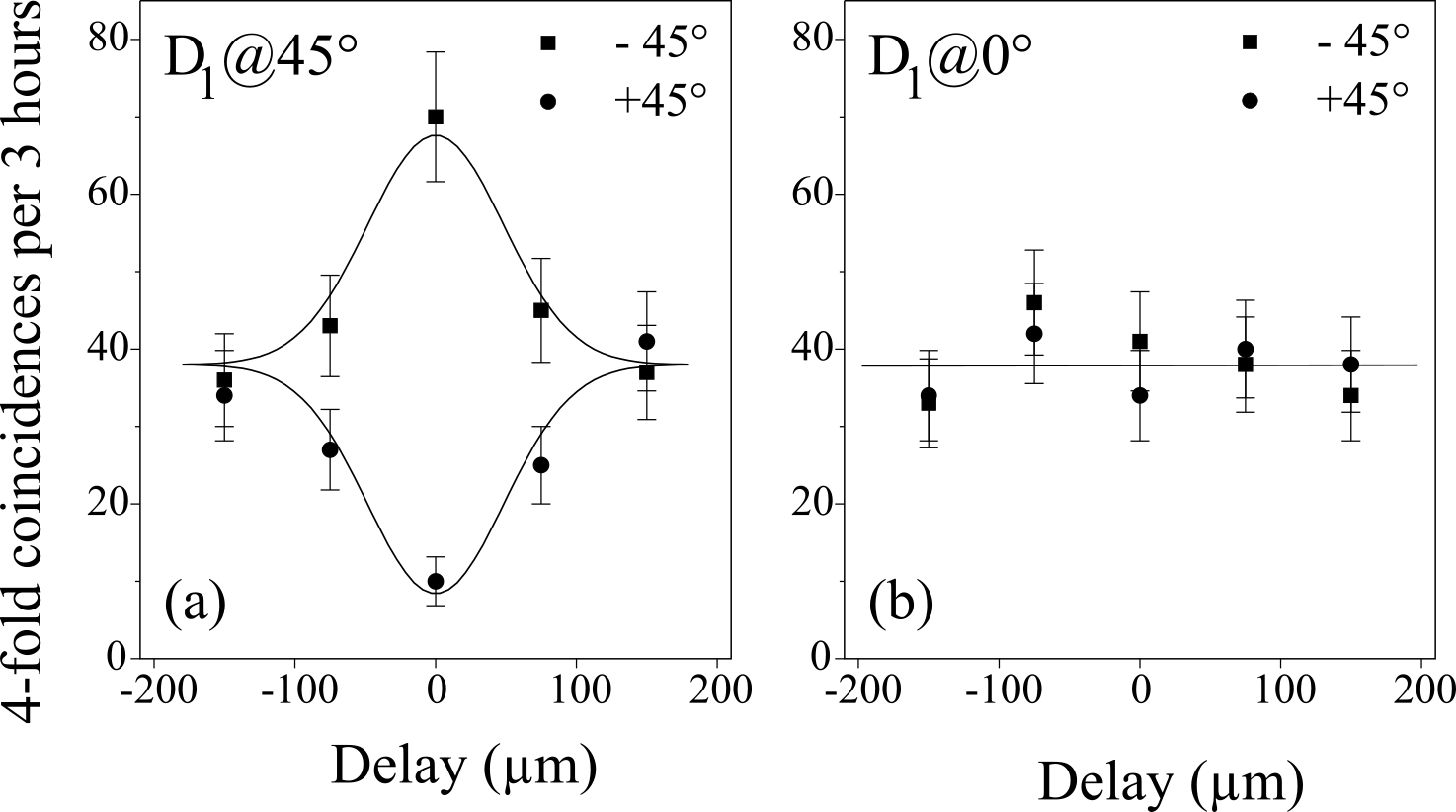
FIG. 2. Experimental confirmation of GHZ entanglement. Graph (a) shows the results obtained for polarization analysis of the photon at , conditioned on the trigger, and the detection of one photon at polarized at and one photon at detector polarized at . The two curves show the fourfold coincidences for a polarizer oriented at and , respectively, in front of detector as a function of the spatial delay in path a. The difference between the two curves at zero delay confirms the GHZ entanglement. By comparison [graph ( b)] no such intensity difference is predicted if the polarizer in front of detector is set at . Error bars are given by the square root of the coincidence counts.