1.5.1. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric downconversion[12]

In the view of quantum engineering, the single photons should be efficiently prepared in a pure state with a single degree of freedom. However, usually the uncontrolled entanglement in the frequency and/or time can significantly degrade the entanglement in the polarization.

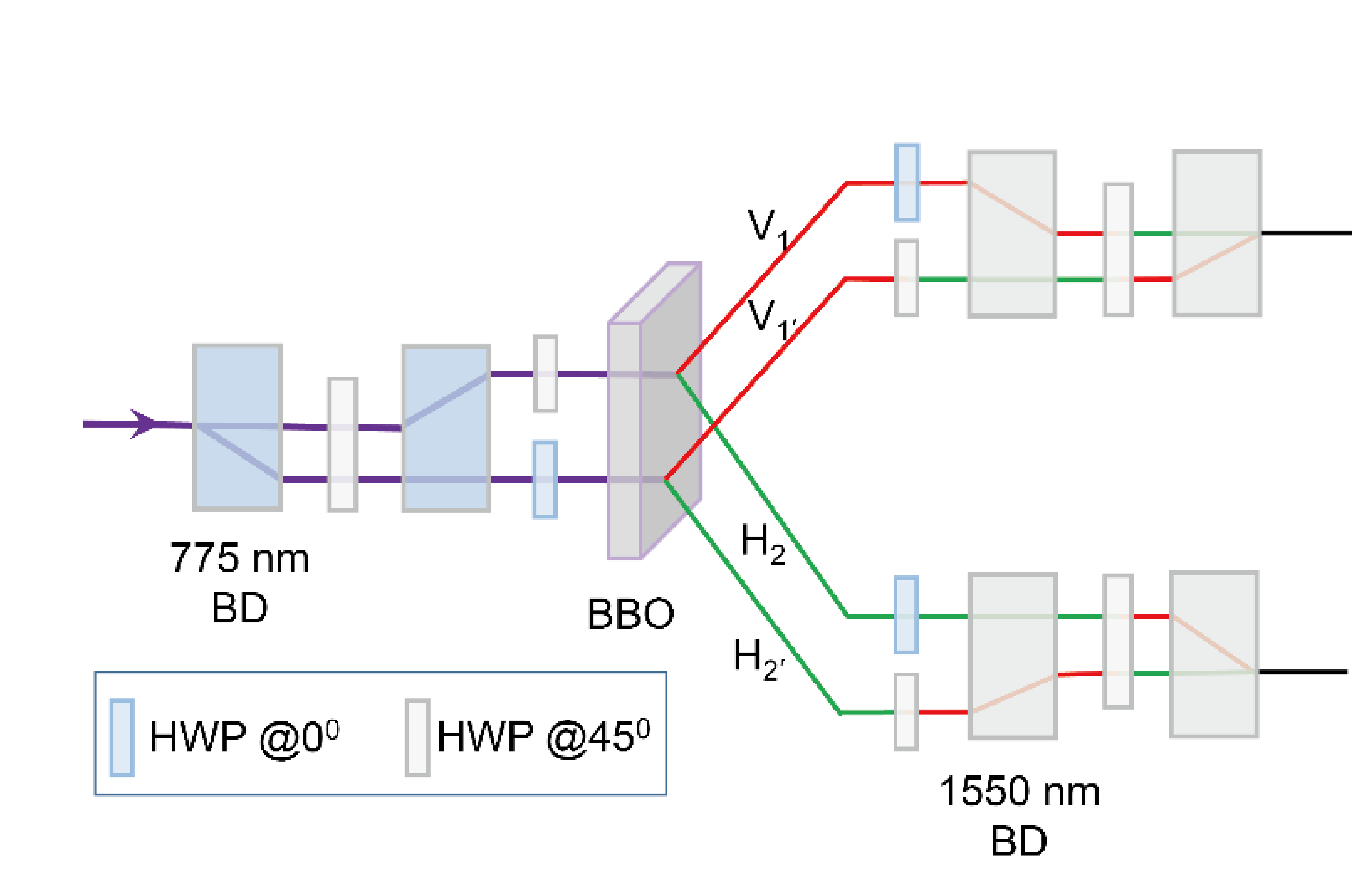
Further, beam-like SPDC was developed with the photon pairs in the form of two separate Gaussian-like beams, which had higher brightness and efficiency coupling into a single spatial mode than those from the non-collinear SPDC where the collection was at intersections of the two down-converted photon rings.

Generally, due to conservation of momentum in SPDC, a lower momentum uncertainty of pump beam can lead to a higher collection efficiency. However, a larger pump beam waist could result in a lower pump energy density. Thus, there is a trade-off between the collection efficiency and brightness.

Thus, by combining our SPDC sources with multiplexing with fast and low-loss switches and suitable optical memories, it is possible to significantly enhance the overall efficiency, opening a new path to large-scale linear optical quantum computing.

The key idea of scattershot boson sampling is to use $k ( k \gg n )$heralded single-photon sources connecting to different input modes of the interferometer, which can achieve an exponential $\left(\matrix{k\\n}\right)$ times increase in the n-photon count rate to compete against the intrinsic probabilistic loss $\sim\varepsilon^n$ .

generate $(|H_1\rangle|V_2\rangle+|V_1\rangle|H_2\rangle)/\sqrt{2}$

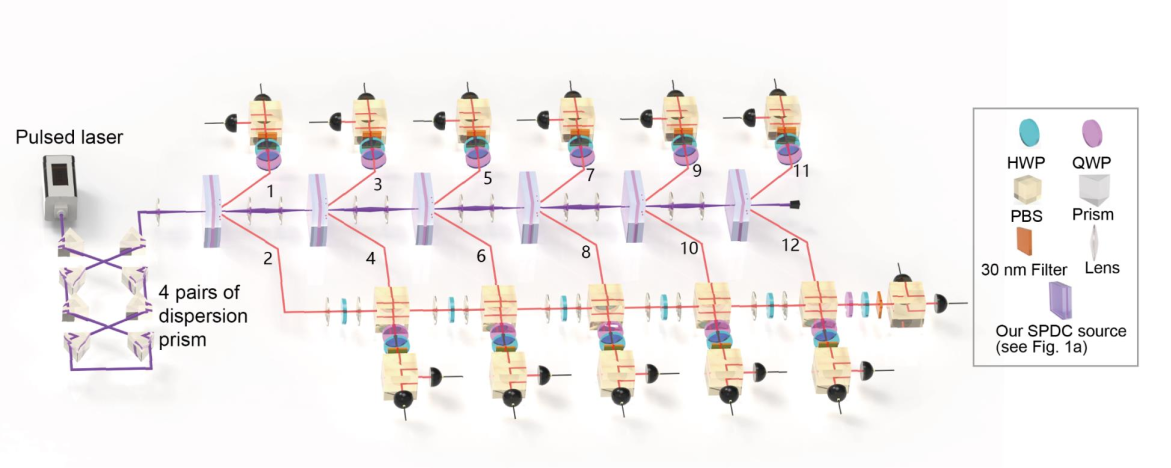
By successively passing the laser through six BBO crystals, we first prepare six pairs of entangled photons. One photon from each pair is combined with the other five photons on a linear optical array of five polarization beam splitters (PBSs) that transmit $H$ and reflect $V$ polarization. Under this arrangement, post-selecting 12-photon coincidences implies that the output photons are either all $H$ or $V$ polarized—two cases are quantum mechanically indistinguishable—thus projecting them into a 12-photon Greenberger-Horne-Zeilinger (GHZ) state in the form of $( |H\rangle^{\otimes 12} | V\rangle^{\otimes 12} ) / \sqrt{2}​$.