RG与临界现象

普适类(Universality classes)

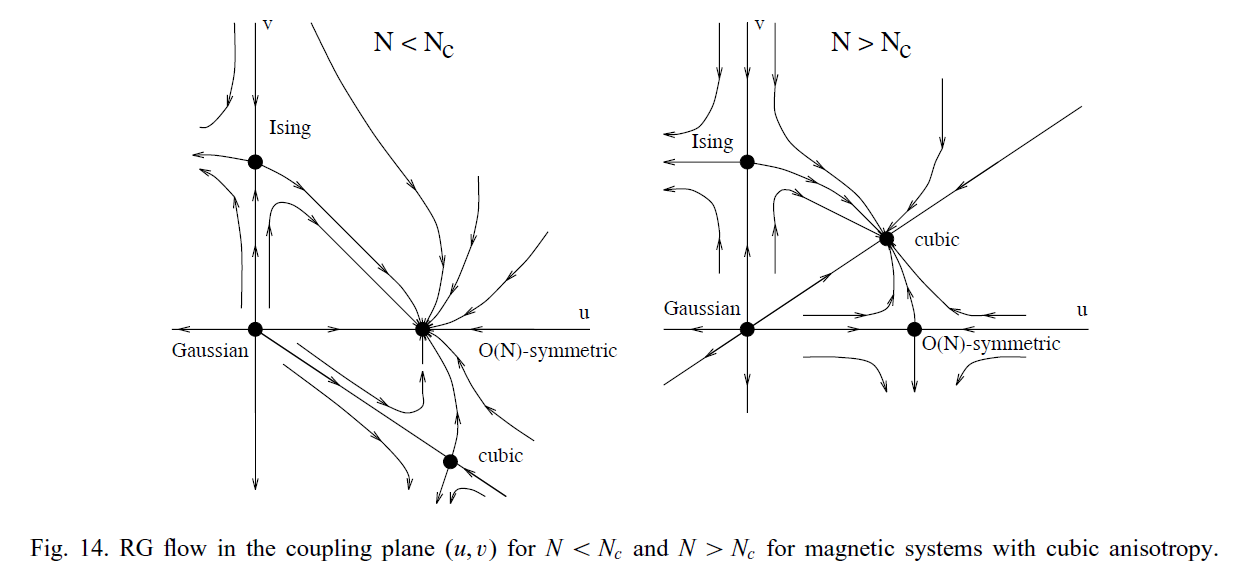
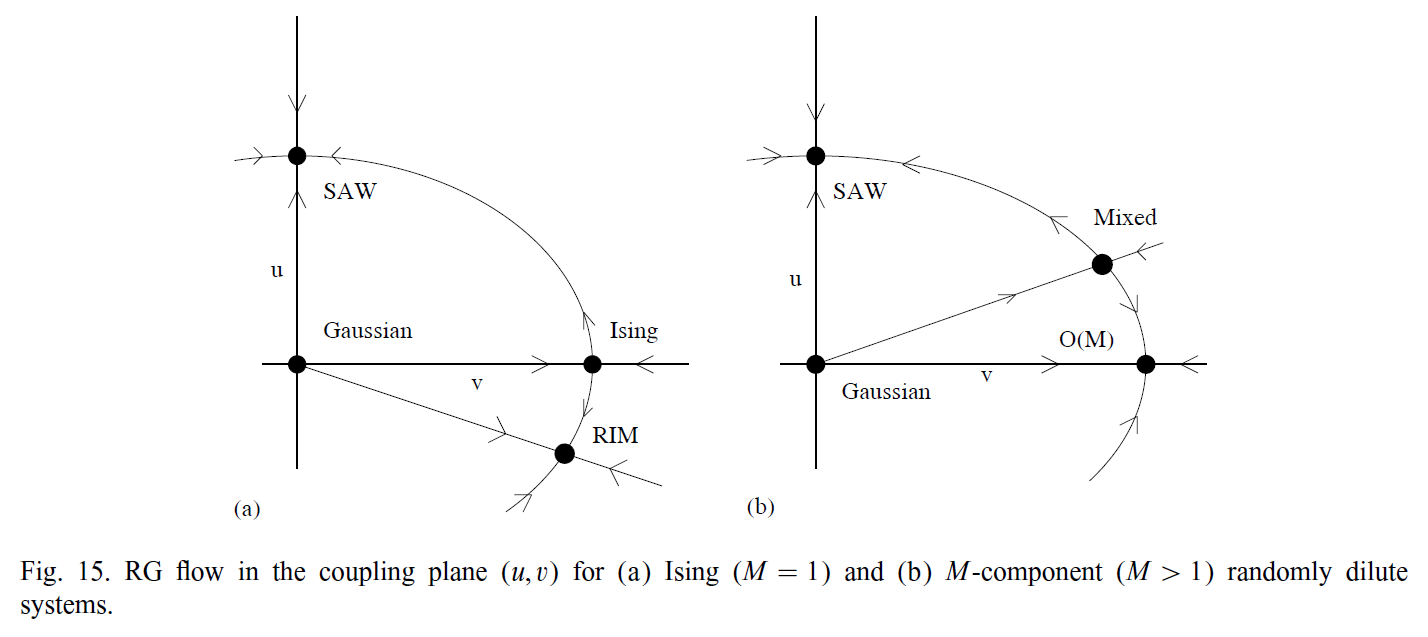
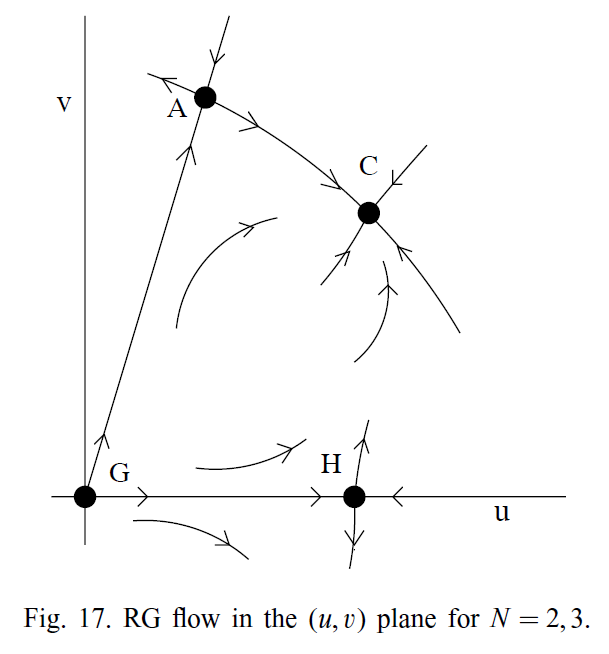
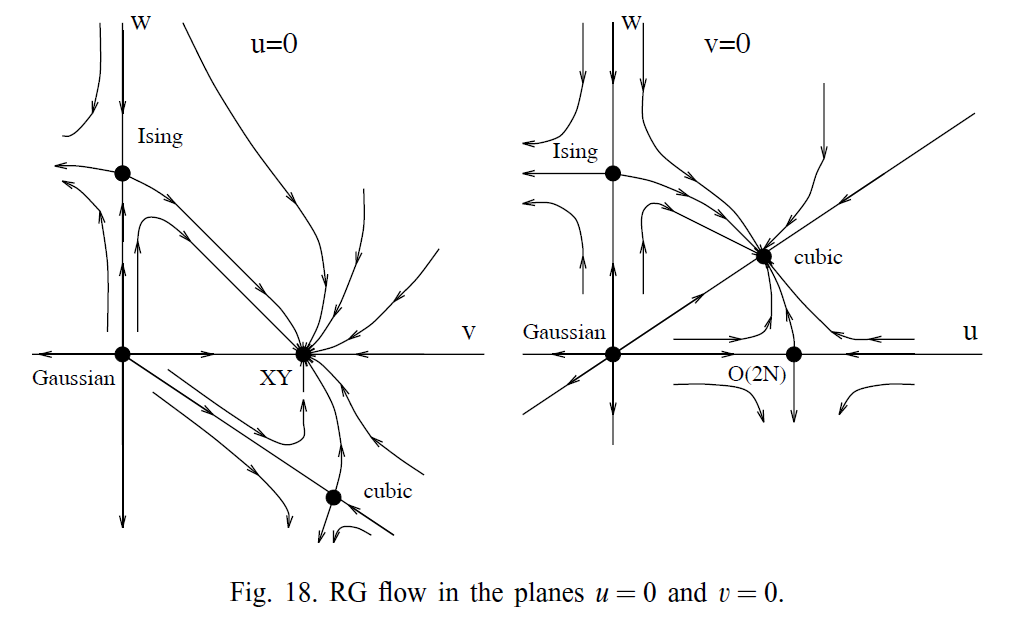
普适类	典型Hamiltonian	relevant models	special properties	critical exponents	equation of state	amplitude ratios	two-point correlation function \(G(x)=\langle\vec{\phi}_{x}\cdot\vec{\phi}_{0}\rangle-\langle\vec{\phi}_{0}\rangle^{2}\)	true correlation length(inverse mass gap) \(\xi_{\mathrm{gap}}=-\limsup _{|x| \rightarrow \infty} \frac{|x|}{\log G(x)}\)	second-moment correlation length \(\xi=\left[\frac{1}{2 d} \frac{\sum_{x}|x|^{2} G(x)}{\sum_{x} G(x)}\right]^{1/2}\)	physical systems
Gaussian class		(1) (2)					high T: Ornstein-Zernike behavior \(G(q)\approx \frac{\chi}{1+q^{2}\xi^{2}}\) low T:			(1) (2)
3D Ising class	\(H=-J\sum_{\langle ij\rangle}s_{i}s_{j}-H\sum_{i}s_{i}, s_{i}=\pm 1\)	(1)Klauder model(bcc); (2)double-Gaussian model(bcc); (3)\(\phi^{4}\)-\(\phi^{6}\) model; (4)improved Blume-Capel model					\textbf{high T}: \(\tilde{G}(q)\approx\frac{\chi}{g^{+}(y)}\), \(y=q^{2}\xi^{2}\) For \(y\to 0\), \(g^{+}(y)=1+y+\sum_{n=2} c_{n}^{+} y^{n}\); For \(y\to \infty\), Fisher-Langer law-\(g^{+}(y)^{-1} \approx \frac{A_{1}^{+}}{y^{1-\eta / 2}}\left(1+\frac{A_{2}^{+}}{y^{(1-\alpha) /(2\nu)}}+\frac{A_{3}^{+}}{y^{1 /(2\nu)}}\right)\) \(G(x) \approx \frac{Z_{\text {gap }}}{2\left(\xi_{\text {gap }}\right)^{d-2}}\left(\frac{2 \pi|x|}{\xi_{\text {gap }}}\right)^{-(d-1) / 2} \mathrm{e}^{-|x| / \xi_{\text {gap }}}\) \textbf{low T}: 同high T			(1)Liquid-vapor transitions (2)Binary mixtures (3)Coulombic systems (4)Micellar systems (5)Uniaxial magnetic systems
2D Ising class	\(H=-J\sum_{\langle ij\rangle}s_{i}s_{j}-H\sum_{i}s_{i}, s_{i}=\pm 1\)						同上			(1)Liquid-vapor transitions (2)Binary mixtures (3)Coulombic systems (4)Micellar systems (5)Uniaxial magnetic systems
3D XY class	(2-component, U(1) symmetry)	(1)liquid \({}^{4}\)He(superfluid transition) (2)BEC		\(\gamma=1.31, \nu=0.67, \eta=0.038\)			形式同上, 数值不同			(1)superfluid transition of \(^{4}\)He(\(\lambda\)-line) (2)
2D XY class	(2-component, O(2) symmetry)	solid-to-solid(SOS) models	BKT critical behavior				\(T=T_{c}\): \(G(r)_{\text{crit}}\sim \frac{(\ln r)^{(2\theta)}}{r^{\eta}}\left[1+O\left(\frac{\ln \ln r}{\ln r}\right)\right]\)		\(\xi\sim \exp\left[\frac{b}{t^{\sigma}}\right]\), \(t\equiv\frac{T-T_{c}}{T_{c}}\), \(\sigma=1/2\)	KT transition: (1)thin films of superfluid helium; (2)easy-plane magnetic materials;
3D Heisenberg class	(2-component, O(3) symmetry)						high T: low T:			(1)Curie transition in isotropic ferromagnets (2)antiferromagnets at the Neel transition point
3D O(\(N\)) class	(\(N\)-component, O(\(N\)) symmetry)	\(N=4\), O(4) - QCD \(N=5\), O(5) - O(3)\(\oplus\)U(1)=O(3)\(\oplus\)O(2), high-\(T_{c}\) superconductors large-N					high T: low T:			(1)isotropic magnets (2)
2D O(\(N\)) class	(\(N\)-component, O(\(N\)) symmetry)	\(N<2\), power-law behavior \(N=2\), BKT transition \(N\leq 3\), no finite-T phase transition					high T: low T:			(1)isotropic magnets (2)

Landau-Ginzburg-Wilson model

模型	Hamiltonian	fixed points	phase diagrams	physical systems
origin LGW Hamiltonian	\(\mathscr{H}=\int \mathrm{d}^{d} x\left[\frac{1}{2} \left(\partial_{\mu} \phi\right)^{2}+\frac{1}{2} r \phi_{i}^{2}+\frac{1}{4 !} \phi^{4}\right]\)	(1)Gaussian; (2)Wilson-Fisher.
cubic anisotropy	\(\mathscr{H}=\int \mathrm{d}^{d} x\left[\frac{1}{2} \left(\partial_{\mu} \phi\right)^{2}+\frac{1}{2} r \phi_{i}^{2}+\frac{1}{4 !} \phi^{4}\right]\)	(1)Gaussian; (2)Ising; (3)O(\(N\))-symmetric; (4)cubic.
random model	\(\mathscr{H}=\int \mathrm{d}^{d} x\left\{\frac{1}{2}\left(\partial_{\mu} \phi(x)\right)^{2}+\frac{1}{2} r \phi(x)^{2}+\frac{1}{2} \psi(x) \phi(x)^{2}+\frac{1}{4 !} g_{0}\left[\phi(x)^{2}\right]^{2}\right\}\) \(\mathscr{H}_{M N}=\int \mathrm{d}^{d} x\left\{\sum_{i, a} \frac{1}{2}\left[\left(\partial_{\mu} \phi_{a, i}\right)^{2}+r \phi_{a, i}^{2}\right]+\sum_{i j, a b} \frac{1}{4 !}\left(u_{0}+v_{0} \delta_{i j}\right) \phi_{a, i}^{2} \phi_{b, j}^{2}\right\}\)	(i)Ising(\(M=1\)) Gaussian, SAW, Ising, RIM; (ii)\(M\)-component(\(M>1\)) Gaussian, SAW, O(\(M\)), Mixed.
frustrated spin systems	\(\mathscr{H}_{\mathrm{STA}}=-J \sum_{\langle v w\rangle_{x y}} \vec{s}(v) \cdot \vec{s}(w)-J^{\prime} \sum_{\langle v w\rangle_{z}} \vec{s}(v) \cdot \vec{s}(w)\)
tetragoal model with 3 couplings	\(\mathscr{H}=\int \mathrm{d}^{d} x\left\{\sum_{i, a} \frac{1}{2}\left[\left(\partial_{\mu} \phi_{a, i}\right)^{2}+r \phi_{a, i}^{2}\right]+\sum_{i j, a b} \frac{1}{4 !}\left(u_{0}+v_{0} \delta_{i j}+w_{0} \delta_{i j} \delta_{a b}\right) \phi_{a, i}^{2} \phi_{b, j}^{2}\right\}\)	(i)\(u=0\) Gaussian, Ising, XY, cubic; (ii)\(v=0\) Gaussian, Ising, O(\(2N\)), cubic; (iii)\(w=0\) Gaussian, O(\(2N\)), XY, tetragonal.
O(\(n_{1}\))\(\oplus\)O(\(n_{2}\)) with \(n_{1}+n_{2}=N\)	\(\mathscr{H}=\int d^{3} x\left[\frac{1}{2}\left(\partial_{\mu} \phi_{1}\right)^{2}+\frac{1}{2}\left(\partial_{\mu} \phi_{2}\right)^{2}+\frac{1}{2} r_{1} \phi_{1}^{2}+\frac{1}{2} r_{2} \phi_{2}^{2}+u_{1}\left(\phi_{1}^{2}\right)^{2}+u_{2}\left(\phi_{2}^{2}\right)^{2}+w \phi_{1}^{2} \phi_{2}^{2}\right]\)	(1)Gaussian; (2)Wilson-Fisher.

USTC| BBS