On multirate rearrangeable Clos networks

参考文献：Du, D. Z., Gao, B., Hwang, F. K., & Kim, J. H. (1998). On multirate rearrangeable Clos networks. SIAM Journal on Computing, 28(2), 463-470.

问题描述

本文研究Clos network的rearrangeability性质的相关问题，转化为图论语言描述如下：

记号

• 考虑带权二部图$G=(V,E)$, 设$G$的两部分别为$A$、$B$（其中$|A|=|B|=r$）。

• 对任意的$e\in E$, 它的权为$w(e)\in [0,1]$.

• $\delta(v)$为顶点$v$的邻居集，$n$为使得$$\sum\limits_{e\in \delta(v)}w(e)\leq n, \forall v\in V$$成立的最小正整数。

• $\mathcal{D}_r^n$为满足

  $$\sum\limits_{e\in \delta(v)}w(e)\leq n, \forall v\in V$$的所有二部图$G=(V,E), V=A\cup B$（$|A|=|B|=r$）构成的集合。

问题

Problem. 求最小的正整数$c$使得$\forall G \in \mathcal{D}_r^n,$ 存在$G$的$c$-边染色使得$\forall v\in V$, $G$中与$v$关联的相同颜色的边的权和不超过$1$.

结果

记所需要的最少颜色数为$M(n,r)$, Chung和Ross在1991年猜想$M(n,r)\leq 2n-1$. 本文证明了

Theorem 8. $M(n, r) ≤ \lceil \frac{17n-5}{16}\rceil$

若我们将$G$中边的权重限制在区间$[b,B]\subseteq [0,1]$中，则对应的所需要的最少颜色数记为$M_{(B,b)}(n,r).$本文还给出了下列结果：

Lemma 1. $M_{(B,0)}(n,r)\leq \frac{n-B}{1-B}.$

Corollary 1. $M_{(1/2,0)}(n,r)\leq 2n-1.$

将权重$> \frac{1}{2}$的边用$n$种颜色染，权重$\leq \frac{1}{2}$的边用$2n-1$种颜色染便能推得：

Theorem 1. $M(n,r)\leq 3n-1.$

证明提要

Lemma 1的证明

证明步骤为：

• 将与$G$中顶点$v$关联的边按照权重从大到小每$m$个分为一组，设一共分成了$q(v)=\lceil \frac{d(v)}{m}\rceil$组。
• 将$v$复制$q(v)$次，得到$v_1,\dots,v_{q(v)},$ 令$v_i$与第$i$组中的边关联，得到的图记为$G^{’}.$
• 用Konig定理给$G^{’}$一个$m$-边染色，导出$G$的一个边染色。
• 令$G$的这个边染色满足bipartite weighted edge coloring problem的条件从而得到$m$的下界。

Proof. 任取$G$中的顶点$v$, 将与$v$关联的边根据权重从大到小的顺序分成$q(v)=\lceil \frac{d(v)}{m}\rceil$组，将这些组分别记为$g_1(v),…,g_{q(v)}(v),$（即权重最大的$m$条边分在第一组，次大的$m$条边分在第二组……）

注意：$g_{q(v)}(v)$中的边数可能少于$m$.

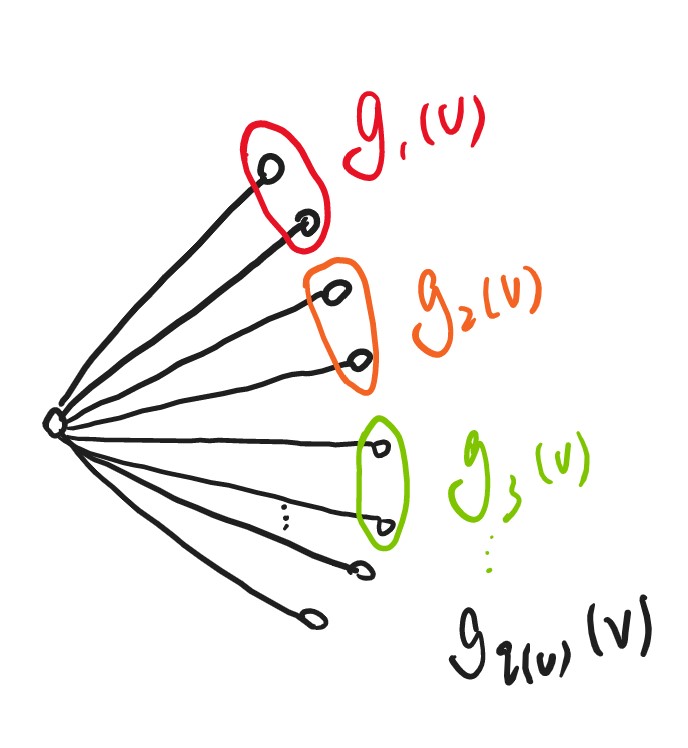
将顶点$v$复制$q(v)$次，得到$v_1,\dots,v_{q(v)},$ 令$v_i$与$g_i(v)$中的边关联，得到的图记为$G^{’},$ 则$G^{’}$的最大度$\leq m.$ 由Konig Theorem知$G^{’}$有一个$m$-边染色，从而可以得到$G$的一个边染色（不一定Proper）。

下面我们考虑当$G$的这个边染色满足"$\forall v\in V$, $G$中与$v$关联的相同颜色的边的权和不超过$1$“时，$m$应当满足的条件。

令$W(v,c)$为与顶点$v$关联的颜色为$c$的边的权重构成的集合，设$W(v,c)$中的元素为$w_1(v, c) ≥ w_2(v, c) ≥ ··· ≥ w_{q(v)}(v, c).$

记$w(v,c)=\sum\limits_{i=1}^{q(v)}w_i(v,c),$ 我们接下来计算$w(v,c)$的与$m$有关的上界，并令其$\leq 1,$ 便可得到$m$的界。

易知

$$w_1(v, c) ≤ B, w_{i+1}(v, c) ≤ w_i(v, c^{’})\text{ for }i =1,…q(v)−1\text{ and any }c^{’}= c.$$

从而对任意的$c^{’} \neq c,$ 有

$$w(v,c)-B\leq w(v,c^{’}).$$

将这些不等式加起来，并加上$w(v, c) −B = w(v, c) −B,$ 便可得到

$$w(v,c)\leq \frac{n}{m}+\frac{m-1}{m}B.$$

令$\frac{n}{m}+\frac{m-1}{m}B \leq 1$便得

$$m\geq \frac{n-B}{1-B}.$$

Theorem 8的证明

在证明之前，我们需要两个重要引理

Lemma 3. Suppose that all weights$ > \frac{1}{f},$ $f$ an integer, are colored by a set $C$ of $c ≥ 2n$ colors. Then at most $\lceil(c − 2)/f − c +2n\rceil$ additional colors are needed which, together with $C,$ color all weights $≤ \frac{1}{f}.$

Lemma 4. Let $G$ be any bipartite graph and suppose $k ≥ 1.$ Then $G$ is the union of $k$ edge-disjoint spanning subgraphs $G_1,…,G_k$ such that $$\lfloor\frac{d_G(v)}{k}\rfloor ≤ d_{G_i}(v) ≤ \lceil\frac{d_G(v)}{k}\rceil\text{ for each }v ∈ G.$$

Theorem 8的证明思路是：

• 首先对每个顶点$i,$ 把与之关联的边的权重划分为Large($w\geq \frac{1}{2}$)、Medium($\frac{1}{2}\geq w> \frac{1}{3}$)和Small($w\leq \frac{1}{3}$)三类，并令$L, M$和$S$分别为这三类边导出的二部子图。
• 对$L$和$M,$ 估算最大度后用Konig Theorem进行染色（并对$M$中的一些边调整颜色）
• 对$S$用Lemma 3进行染色。

Proof of Theorem 8.

设与顶点$i$关联的$L, M$和$S$中的边的条数分别为$l_i, m_i$和$s_i.$ 易知

$$\frac{l_i}{2}+\frac{m_i}{3}\leq n$$

即

$$m_i \leq 3n-\frac{3l_i}{2}.$$

由Lemma 4, $M = M_1∪M_2∪M_3,$ 其中$d_{M_j}(i)\leq \lceil n-l_i/2\rceil.$ 令$L^{’}=L\cup M_1\cup M_2,$ 则$L^{’}$的最大度为

$$\max\limits_i \{l_i+2\lceil n-l_i/2\rceil\}\leq 2n+1.$$

从而可以用$2n+1$种颜色给$L^{’}$染色。

$M_3$的最大度为

$$\max\limits_i \{\lceil n-l_i/2\rceil\}\leq n.$$

从而可以用$\lceil \frac{n}{2}\rceil$种颜色给$M_3$染色。

现在一共用了至多$2n+1+\lceil \frac{n}{2}\rceil\leq \frac{5n+3}{2}$种颜色。

由Lemma 3($f=3$)知还需要$\lceil \frac{(5n-1)/2}{3}-\frac{5n+3}{2}+2n\rceil=\lceil \frac{n-5}{3} \rceil$种颜色。从而总共需要的颜色数至多为$\frac{17n+3}{6}$（此处原文中计算有误。）