Improved bounds on nonclocking 3-stage Clos networks

问题描述

这是一篇考虑Clos network的rearrangeability和nonblocking性质的文章，问题用图论语言描述如下：

记号

• 考虑带权二部图$G=(V,E)$, 设$G$的两部分别为$A$、$B$（其中$|A|=|B|=r$）。

• 对任意的$e\in E$, 它的权为$w(e)\in [0,1]$.

• $\delta(v)$为顶点$v$的邻居集，$n$为使得$$\sum\limits_{e\in \delta(v)}w(e)\leq n, \forall v\in V$$成立的最小正整数。

• $\mathcal{D}_r^n$为满足

  $$\sum\limits_{e\in \delta(v)}w(e)\leq n, \forall v\in V$$的所有二部图$G=(V,E), V=A\cup B$（$|A|=|B|=r$）构成的集合。

问题

Problem. 求最小的正整数$c$使得$\forall G \in \mathcal{D}_r^n,$ 存在$G$的$c$-边染色使得$\forall v\in V$, $G$中与$v$关联的相同颜色的边的权和不超过$1$.

主要结果

记所需要的最少颜色数为$M(n,r)$, Chung和Ross在1991年猜想$M(n,r)\leq 2n-1$. 本文给出的主要结果是

Theorem 1. $M(n, r) ≤ 2.557n + o(n) $

证明方法

首先我们有一个简单的结果

Lemma 2.(Du et al. ) Consider $G = (V, E) ∈ \mathcal{D}_r^n$ with bipartition $V = A∪B$ and assume that we have used at least $\frac{2n}{1-\alpha}$ colors to color all edges except some edges $e$ with $w(e) ≤ α.$ Then we can greedily color these remaining edges without using any additional color.

In particular, if $M_{(α,1]}(n, r) \leq \lceil2n/(1 - α)\rceil$ , then $M(n, r) ≤ \lceil2n/(1 - α)\rceil$ .

即只要我们能用$\frac{2n}{1-\alpha}$种颜色染好所有权大于$\alpha$的边，则权$\leq \alpha$的边可以被贪婪地染好。

Proof. If $e = (u, v) ∈ E$ with $w(e) ≤ α$ cannot be colored then the total weight of edges of a given color $i$ incident to either $u$ or $v$ is greater than $1 − α$. Summing over all $\frac{2n}{1-\alpha}$colors, we get a contradiction with sum of conditions $\sum\limits_{e\in \delta(v)}w(e)\leq n, \forall v\in V$ for $u$ and $v.$

概要

根据Lemma 2，我们只需关注所有边的权都$\in [\alpha,1]$的图$G$，并且用至少$\lceil2n/(1 - α)\rceil$种颜色去染它。

具体证明过程如下：

令$G\in \mathcal{D}_r^n$（即$G$中所有边的权都$\in [\alpha,1]$）

• 1、运用Balanced decompositions将$G$的边集$E$划分成一些子集$F_1, . . . , F_p$的并使得$G[F_i]$满足一些好的最大度条件，
• 2、运用Konig Theorem把每个$F_i$分解成一些匹配（Matchings）的并，并记每个匹配中的边的最大权为该匹配的size.
• 3、考虑由这些匹配作为items的Associated bin packing problem, 求解得到这些匹配的最优染色方案，进而得到$G$的染色方案。

Balanced decompositions of bipartite graphs

这里主要证明了

Theorem 4. Consider a bipartite graph $G = (V, E)$ and let $γ_1, . . . , γ_l ∈ (0, 1)$ such that $\sum\limits_{i=1}^{l}\gamma_i=1$. Then there exists a partition $E_1, . . . , E_l$ of $E$ such that for all $v ∈ V$ and all $i = 1, . . . , l$,

$$γ_i deg_E(v) - e_i(v) < deg_{E_i}(v) < γ_i deg_E(v) + e_i(v).$$

Here $e_i(v) < 3$, and$\sum\limits_{i=1}^{l} e_i(v) ≤ 2(l - 1).$

证明的思路是首先我们可以用整数流的方法证明$l=2$的情况：

Lemma 3 (Hoffman). Consider a bipartite graph $G = (V, E)$ and let $0 ≤ µ_1, µ_2$ with $µ_1 + µ_2 = 1.$ Then, there exists a partition of $E$ into $E_1$ and $E_2$ such that: $µ_i deg_E(v) ≤ deg_{E_i}(v) ≤ µ_i deg_E(v).$ for $i = 1, 2$ and all $v ∈ V .$

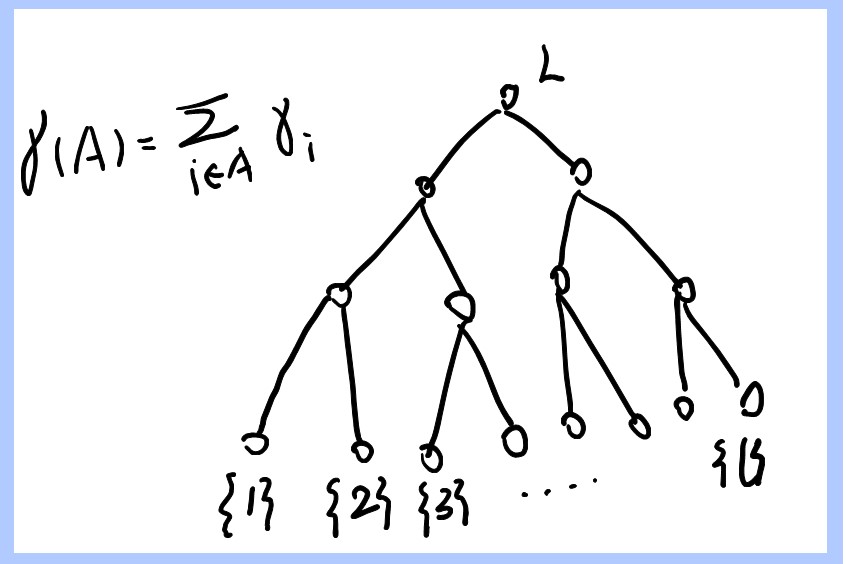
接着再利用类似二分法的方法，考虑root的标号为$L={1,2,\dots,l}$的二叉树$T$。在该二叉树中，每个顶点有两个子顶点，子顶点的标号为父顶点标号$F$的两个子集$S_1$, $S_2$，并且$\sum\limits_{i\in S_1}\gamma_i$与$\sum\limits_{i\in S_2}\gamma_i$尽可能接近。

令标号为$L$的顶点对应的边集为$E$, 在$T$的每一层中运用Lemma 3（$\mu_1,\mu_2$分别为子顶点的标号集合里$\gamma_i$的和）将父顶点对应的边集划分成两个子集的并，并将这两个子集对应到两个子顶点。

如$T$的第二层中的两个子顶点对应的边集分别为Lemma 3中的$E_1$和$E_2$.

这样便得到了我们想要的划分。

Partitioning the graph

有了Theorem 4后我们便可以将$E$划分成$F_1,\dots,F_q$使得每个$G[F_i]$的最大度得到控制，从而可以对每个$F_i$使用Konig Theorem.

首先取$α_0 = 1 > α_1 > α_2 >. . . > α_p = α ≥ 0$, 令

$$D_i = \{e ∈ E : w(e) ∈ (α_i, α_{i-1}]\},i=1,\dots,p.$$

再对每个$D_i$运用Theorem 4将$D_i$分解成$D_i^1\cup \dots\cup D_i^i$, 其中$γ^i_1=\frac{1}{\alpha_1}α_i, γ^i_2= (\frac{1}{\alpha_2}-\frac{1}{\alpha_1})α_i, . . . , γ^i_i = (\frac{1}{\alpha_i}-\frac{1}{\alpha_{i-1}})α_i$.

最后令$F_k = D_k^k ∪D^k_{k+1} ∪ · · · ∪ D_p^k$, 如图

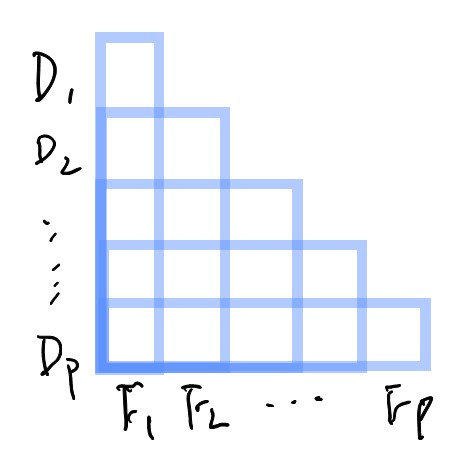
经过计算便可得到

The associated bin packing problem

我们运用Konig Theorem将$F_k$分解成匹配的并，并令每个匹配的size为其中边的最大权。现在我们将这些匹配装到一些容量为$1$的bin中, 每一种装法给出图$G$的一种染色（即每个bin代表一种颜色），从而我们只需计算需要的最少的bin的数目。

我们知道size$> 1-\alpha$的匹配只能独占一个bin, 所以我们令$\alpha_1=1-\alpha.$ 从而我们便可将问题转化为下面的Bin packing problem

在构造Bin packing problem时我们丢弃了至多$\frac{3}{2}p(p+1)$个匹配，我们给每个这样的匹配一个单独的bin.

那么这样一个Bin packing problem有一个平凡的下界

$$\frac{n}{1-\alpha}+\sum\limits_{k=2}^{p}\alpha_{k-1}(\frac{1}{\alpha_k}-\frac{1}{\alpha_{k-1}})n.$$

经过计算我们得到由本文的方法得到的$M_{[α,1]}(n, r)$的上界最好只能是

$$\min\limits_{\alpha\in (0,1]}\max(\frac{2n}{1-\alpha},\frac{n}{1-\alpha}+n\log(\frac{1-\alpha}{\alpha}))=Mn.$$

其中$2.5569 ≤ M ≤ 2.5570.$

最后本文运用了类似积分的方法证明了这个界是可以达到的，即所需要的颜色$\leq M · n + O(p^2) + O (n/p).$