曲线拟合——cftool

在大物实验中常常遇到这么一类实验，需要根据实验数据进行数据拟合，从中得到相应的物理规律，使用计算机辅助计算作图可以使我们的工作更加方便准确，这里介绍使用matlab工具箱cftool进行曲线拟合的方法和一些实际使用中个人的小技巧。

一、cftool简介

cftool是matlab用于数据拟合的工具箱，功能强大，使用简便。

二、cftool的使用

(一) 数据的导入

1、手动输入

可以直接从命令行用一维向量形式输入数据进行导入

2、从excel文件导入

matlab也可以通过excel文件导入数据

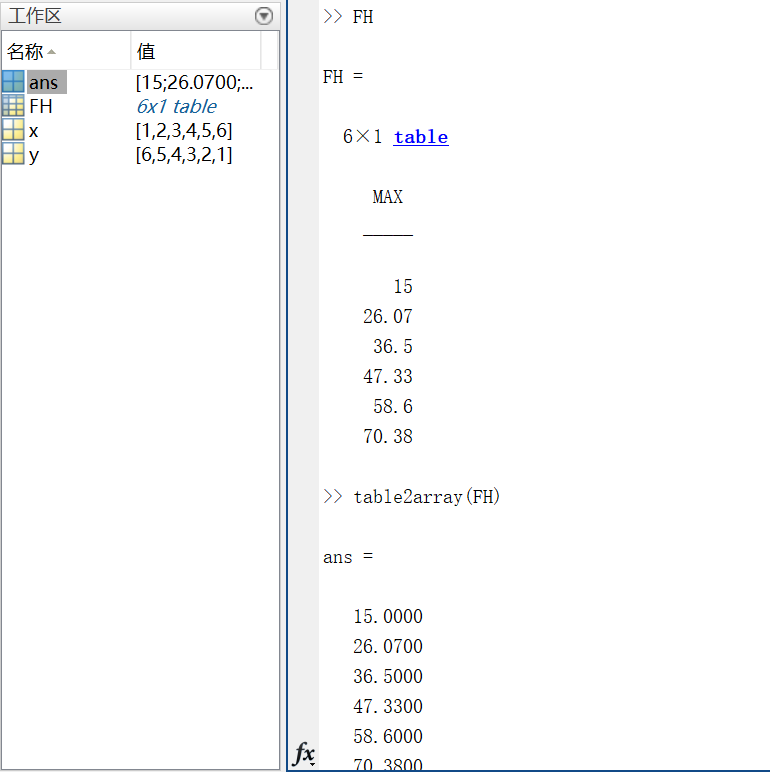
导入后会得到一个以文件名命名的table表格类型变量，需要使用table2array转化为矩阵变量，注意不能导入非数值变量（导入的非数值变量会自动变成NaN），而且导入两列会生成N*2的表格。

(二) 拟合方式的选择

在命令行直接输入cftool可以调出cftool工具箱界面

各拟合方式如下：

1、Custom Equation（常用来画需要求方程的曲线）

用户自定义的函数类型

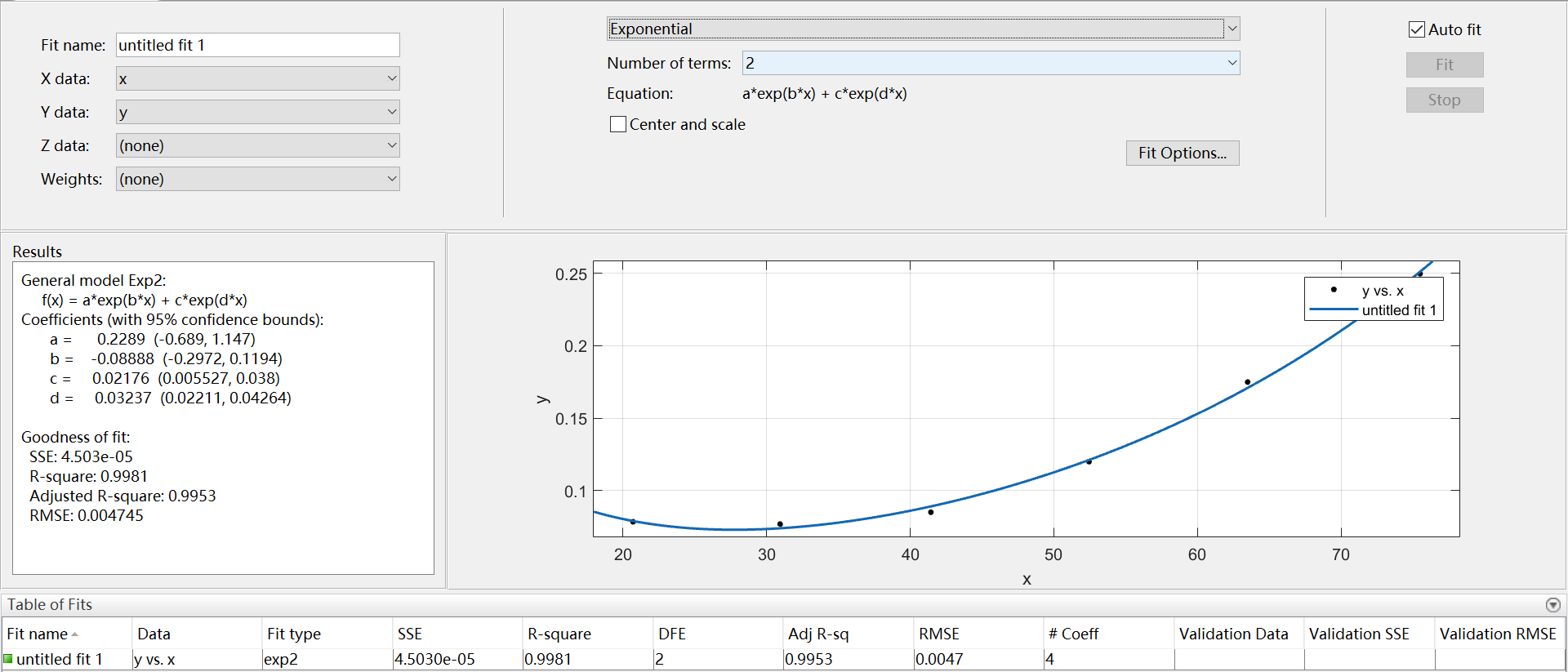
2、Exponential

指数逼近，有2种类型： $ae^{bx}$ 、 $ae^{bx}+ce^{dx}$

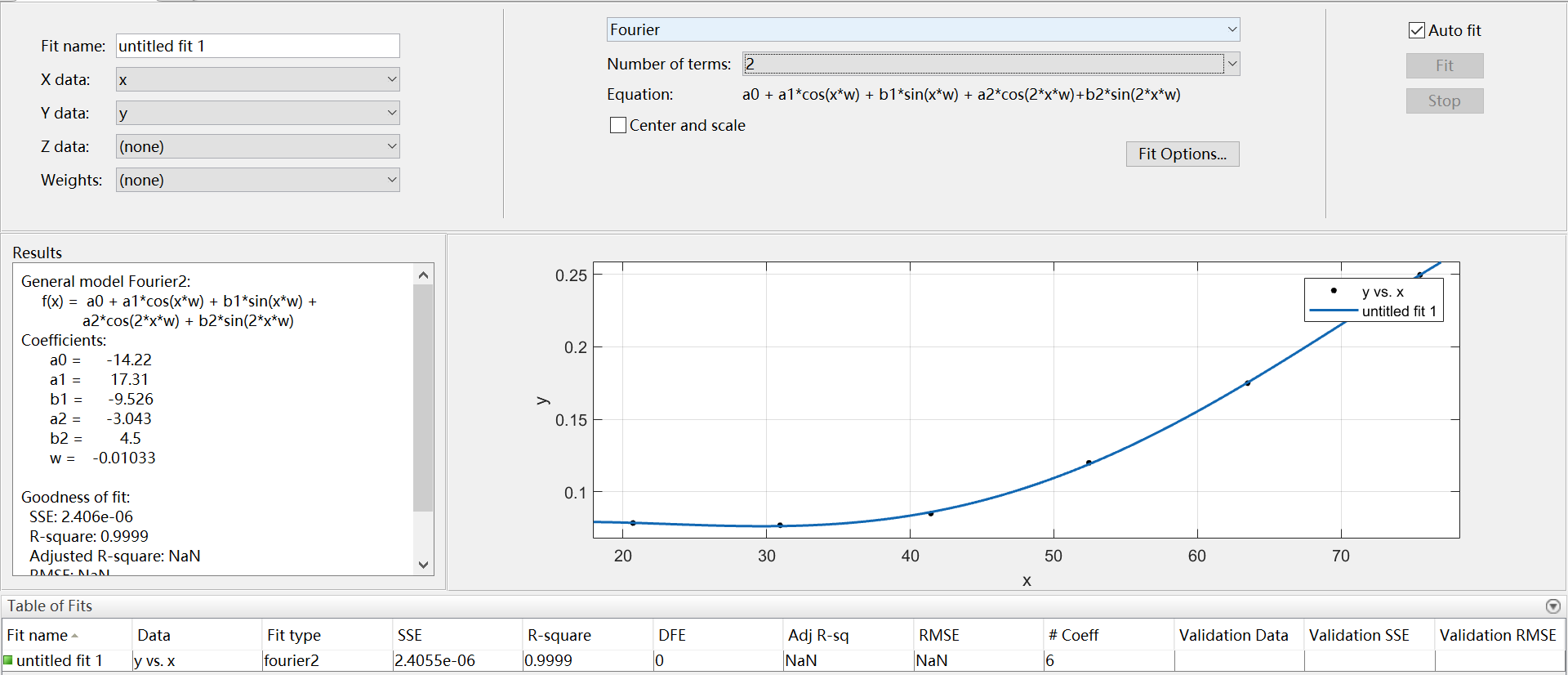
3、Fourier

傅立叶逼近，有7种类型，基础型是 $a_0 + a_1cos(wx) + b_1sin(wx)$

4、Gaussian

高斯逼近，有8种类型，基础型是 $a_1e^{-(\frac{x-b1}{c1})^2}$

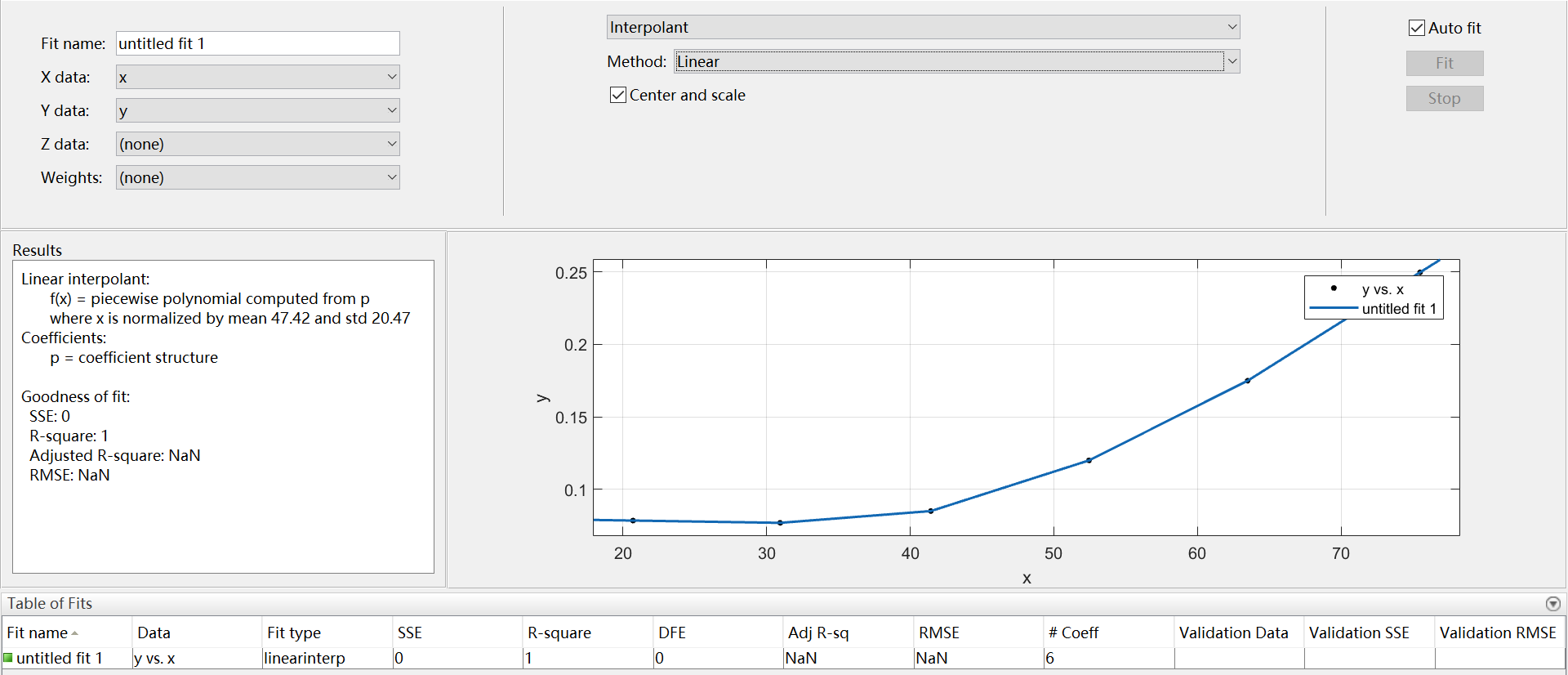
5、Interpolant（常用来线性插值画折线图）

插值逼近，有4种类型，linear、nearest neighbor、cubic spline、shape-preserving (线性、最近邻、三次样条、保形)

折线图(linear)

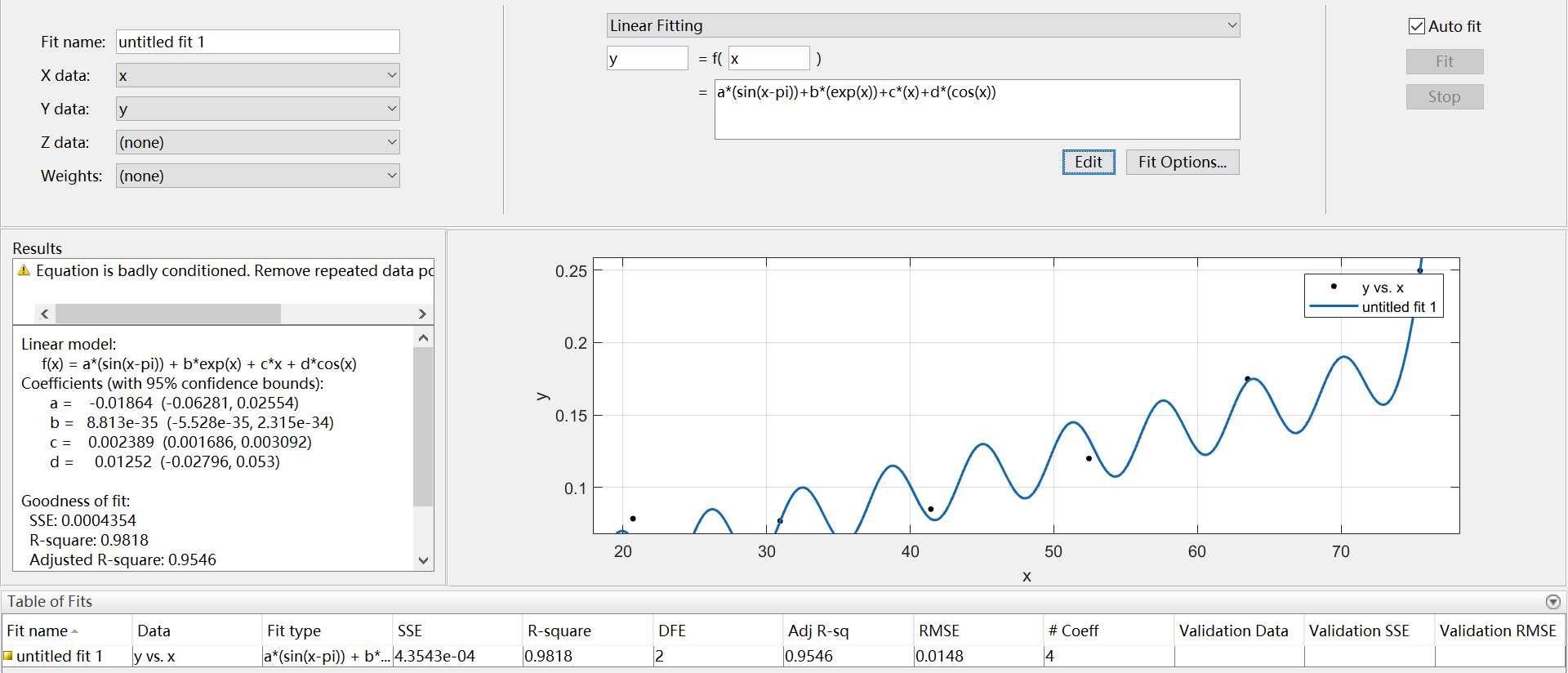
6、Linear Fitting

线性拟合，可以自定义一组基础型，用这些基础型的线性组合进行逼近

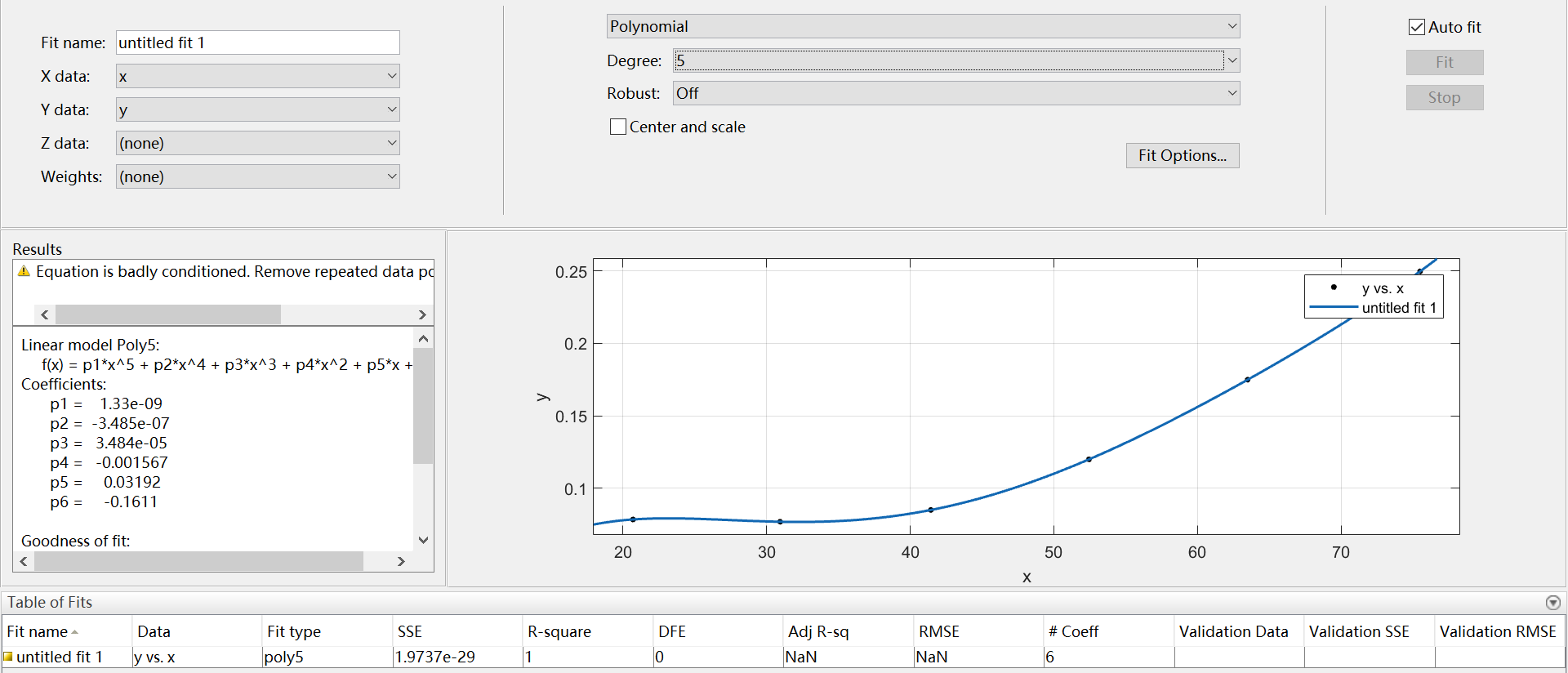
7、Polynomial

多形式逼近，有9种类型，linear ~、quadratic ~、cubic ~、4-9th degree ~

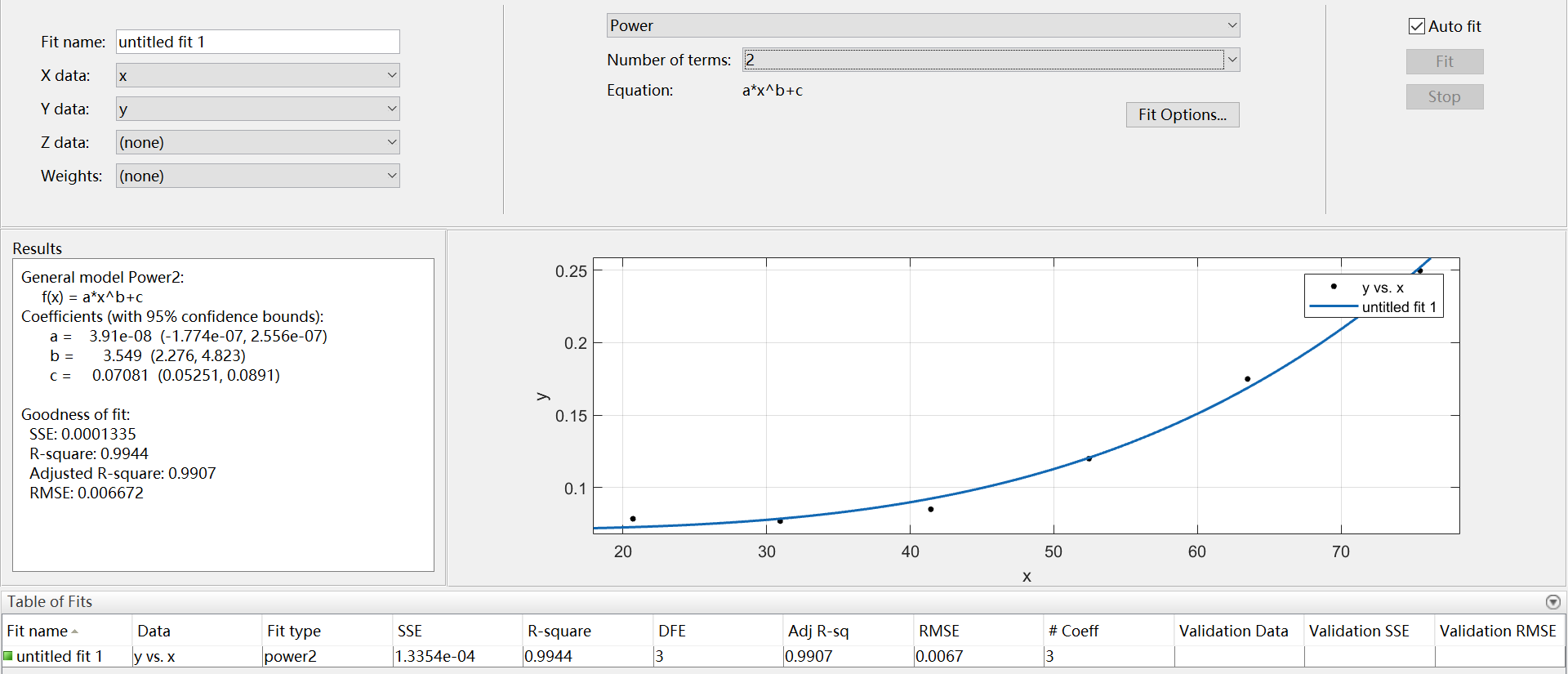
8、Power

幂逼近，有2种类型， $ax^b$ 、 $ax^b + c$

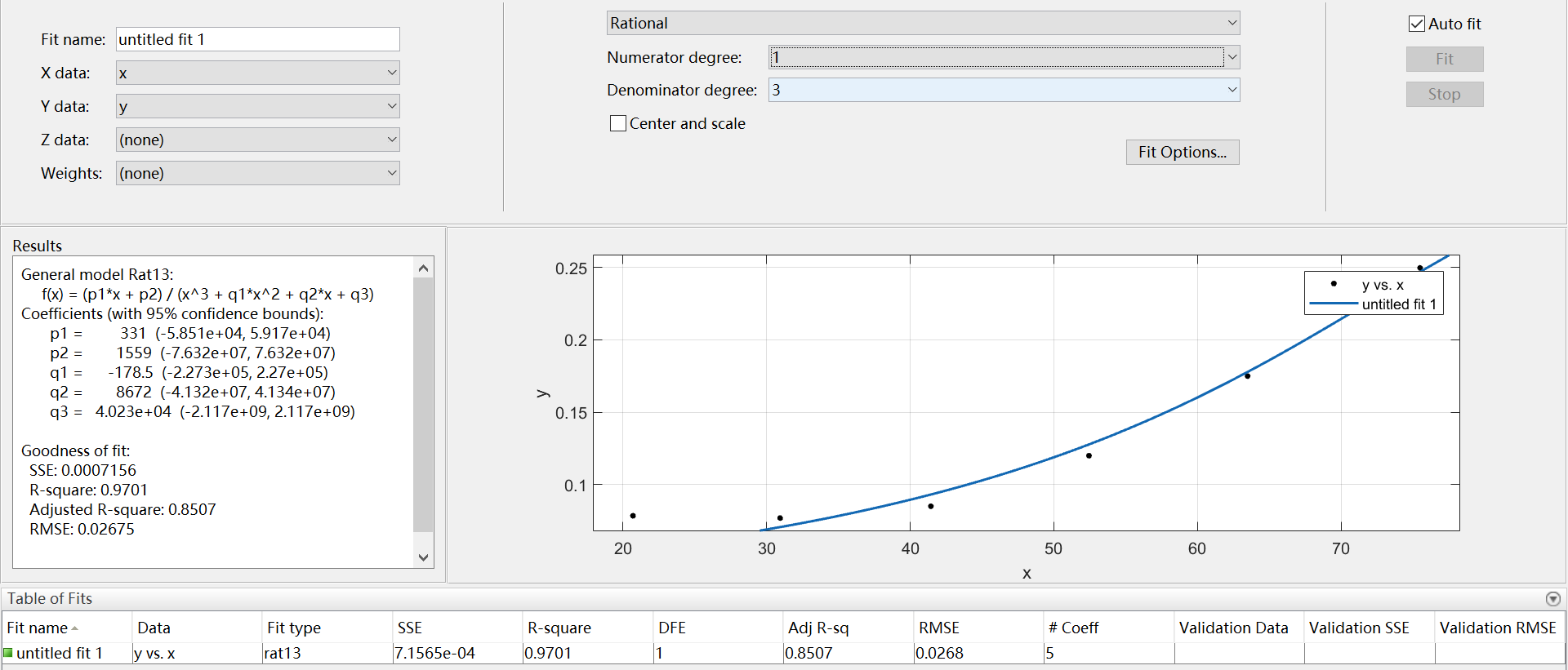
9、Rational

有理数逼近，分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~；此外，分子还包括constant型

10、Smoothing Spline（常用来画不需要求方程的曲线）

平滑逼近，用光滑曲线拟合数据

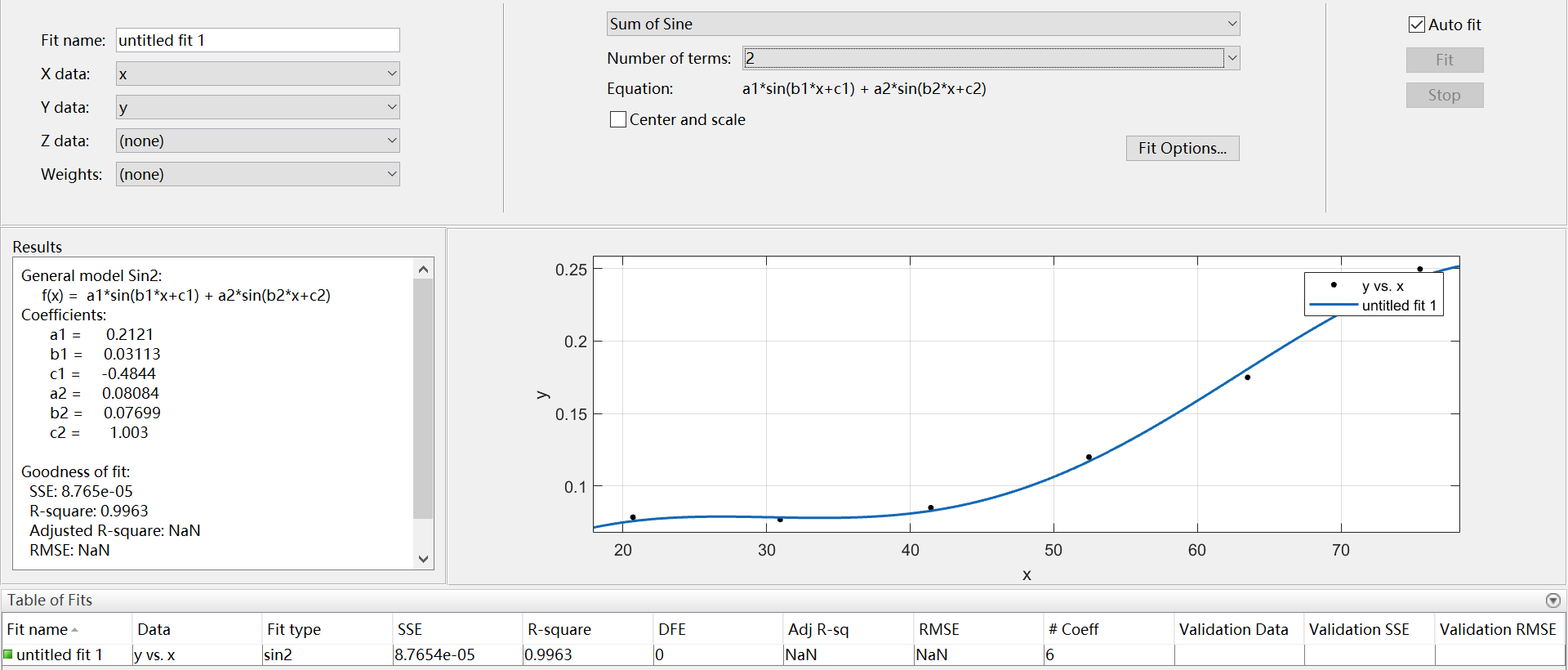
11、Sum of Sin Functions

正弦曲线逼近，有8种类型，基础型是 $a_1sin(b_1x + c_1)$

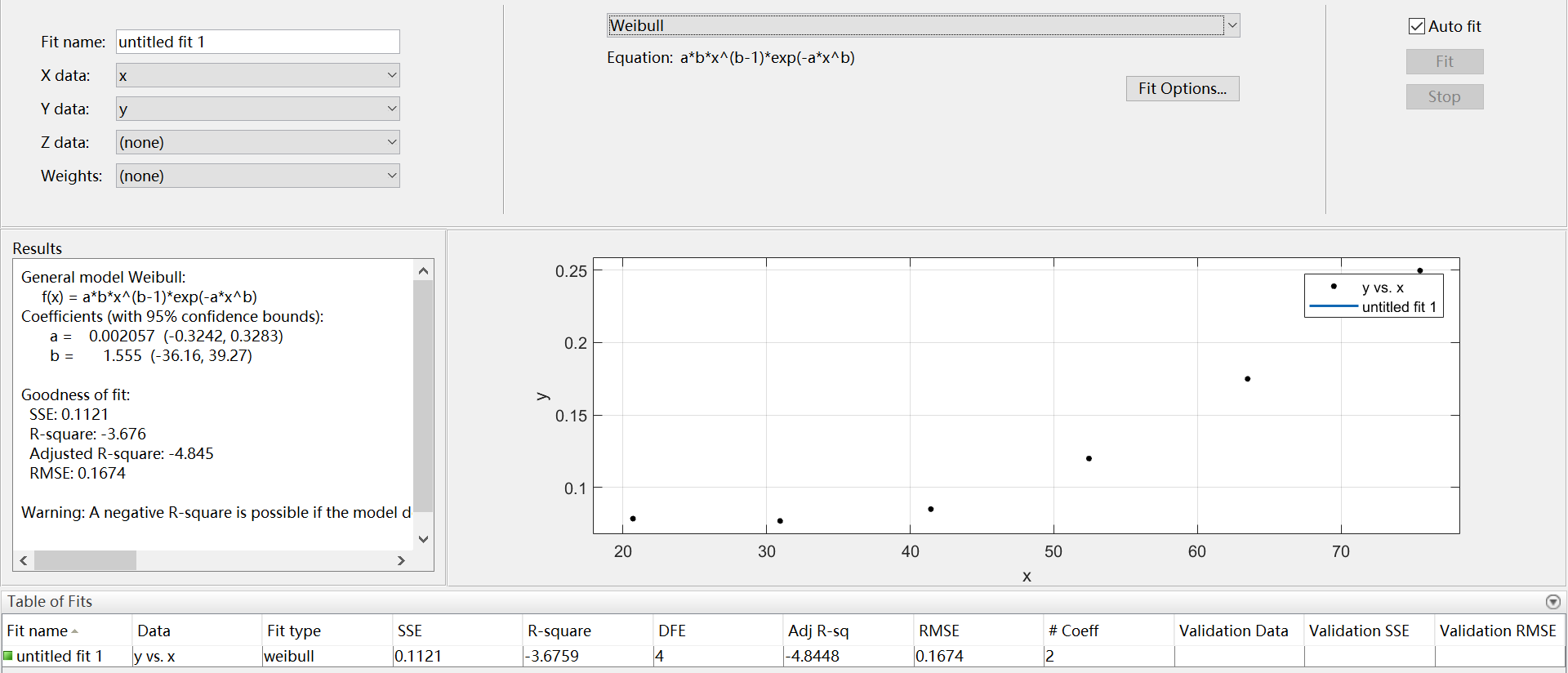
12、Weibull

用 $y=ab*x^{b-1}e^{-ax^b}$ 进行拟合

(三) 拟合优度

SSE：错误的平方和。此统计量测量响应的拟合值的偏差。接近0的值表示更好的匹配。

R-square：多重测定系数。数值的大小在0到1之间，越接近1，表明方程的变量对y的解释能力越强。

Adjusted R-square：自由度调整 r 平方。接近1的值表示更好的匹配。当向模型中添加附加系数时, 它通常是适合质量的最佳指示器。

RMSE：均方根误差。接近0的值表示更好的匹配。

(四) 其他技巧

模型设计拟合好之后选择菜单中的”文件“→”Print to Figure“进行下一步操作。

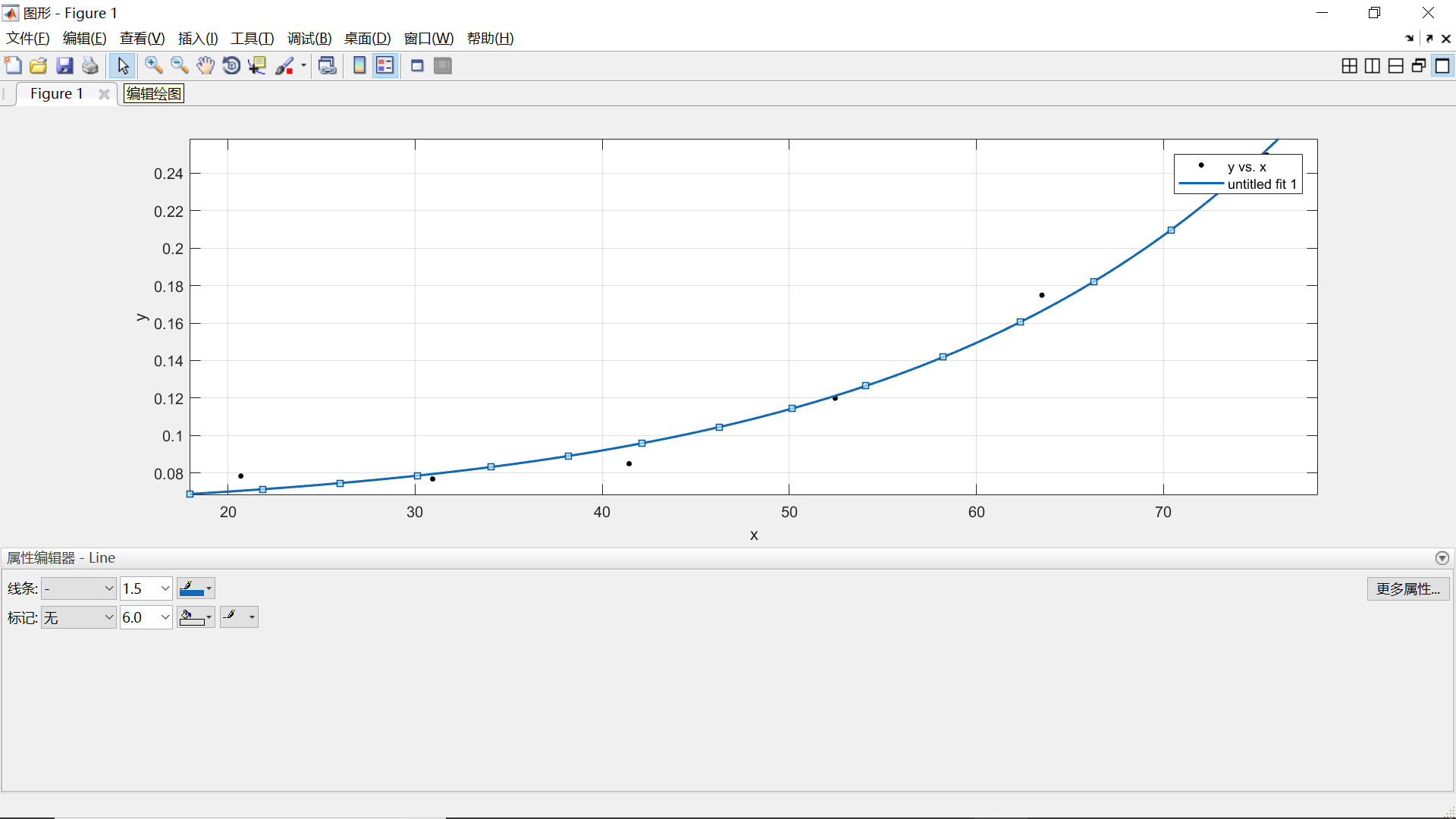
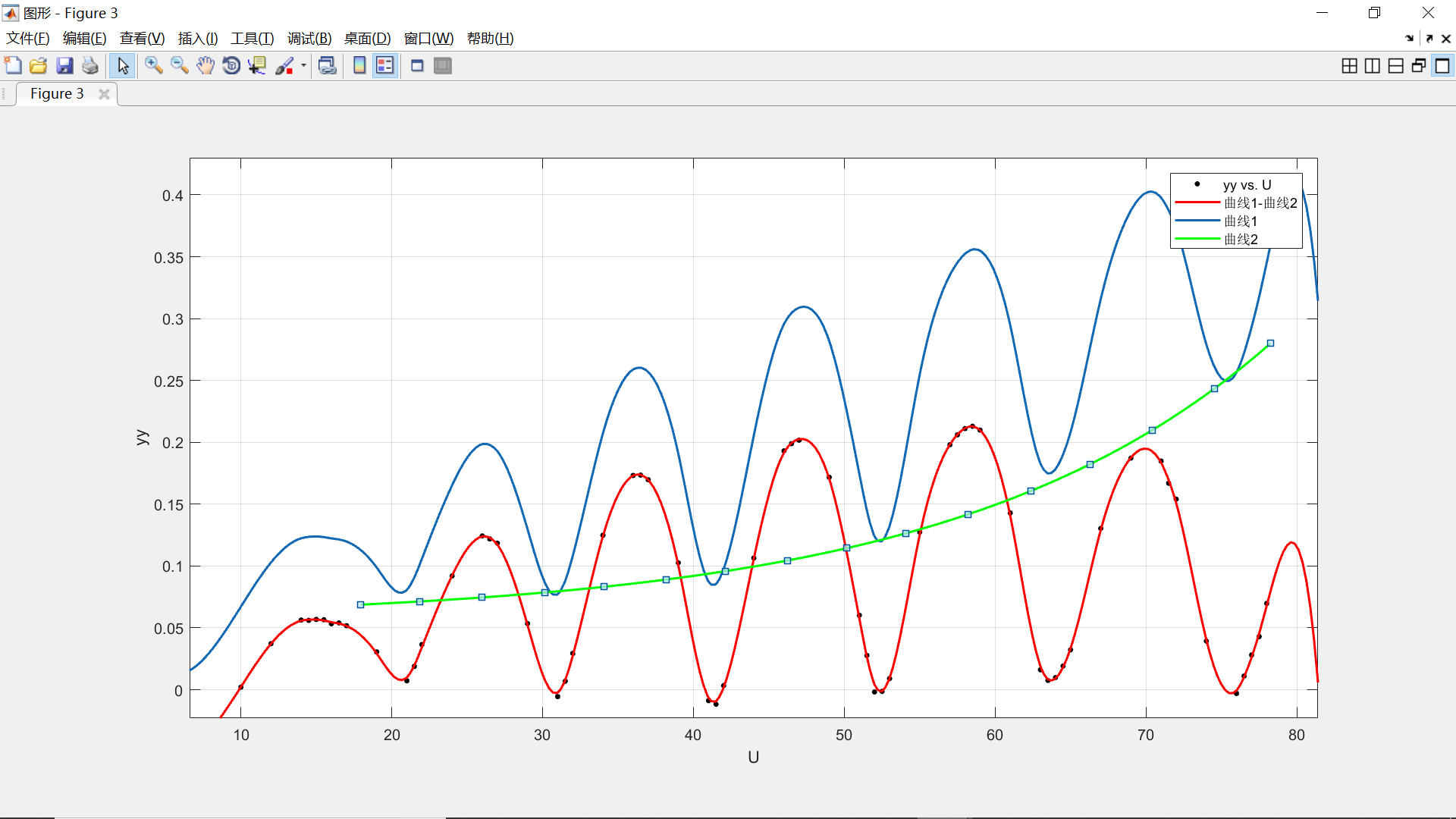
1、将多条曲线放在一幅图内

cftool似乎没有直接可以将多条曲线Print到一幅Figure的方法（据我所知），但cftool支持图像的复制粘贴。故欲将多条曲线放在同一幅图内可以通过选定一幅图的曲线复制到另外一幅图里实现（先点击编辑绘图才能进行曲线选定和复制粘贴）。

2、读取曲线上点的坐标

使用菜单栏中的”工具“→”数据游标“

3、曲线相减

可以用数据差去拟合（若数据数不同可以用曲线方程进行转化）